Roger Penrose

Guinea 2010  Michel 7617                                                       Macao 2007  Michel 1544


Mathematiker, die einen Nobelpreis gewonnen haben

Bekanntermaßen gibt es keinen Nobelpreis für Mathematik  -  statt dessen werden der Abel-Preis, die Fields-Medaille und andere Auszeichnungen verliehen. Aber zahlreiche Mathematiker haben einen Nobelpreis erhalten. Alle Preise außer dem Friedensnobelpreis gingen bereits an Mathematiker, also für Physik, Chemie, Medizin, Literatur und Wirtschaft. In einer losen Reihe sollen diese Preisträger hier von Zeit zu Zeit vorgestellt werden. Naturgemäß haben die Mathematiker, die einen Nobelpreis verliehen bekamen, weitere Meriten in einem anderen Gebiet erworben. Oft handelt es sich um Wissenschaftler, die sich nach ihrem Mathematikstudium einem naturwissenschaftlichen Anwendungsgebiet zugewandt haben. Am häufigsten findet man jedoch Mathematiker unter den Preisträgern des Nobelpreises für Wirtschaftswissenschaften. In diese Reihe sollen auch Wissenschaftler aufgenommen werden, die aus anderen Disziplinen stammen, aber wichtige Beiträge für die Mathematik geliefert haben. Die Reihe ist dadurch limitiert, dass es nicht von allen Nobelpreisträgern Briefmarken gibt. Aber erfreulicherweise kommen immer noch neue hinzu.

Südafrika 1996   Michel 1027   Scott 955c

→   Folge 1   Russell   (Literatur)         →   Folge 2   Bardeen   (Physik)         →   Folge 3   Tinbergen   (Wirtschaft)         →   Folge 4   Cormack   (Medizin)         →   Folge 5   Lorentz   (Physik)         →   Folge 6   Solschenizyn   (Literatur)         →   Folge 7   Echegaray   (Literatur)         →   Folge 8   Einstein   (Physik)

Folge 9    Roger Penrose
           (* 1931, Nobelpreis für Physik 2020)


Roger Penrose ist ein englischer Mathematiker. Er studierte in Cambridge und arbeitete zunächst an mehreren Universitäten, u.a. in London, Cambridge und Princeton, bevor er 1973 Rouse Ball Professor in Oxford wurde und diesen Lehrstuhl 25 Jahre lang innehatte. Seine frühen Publikationen behandeln Probleme der reinen Mathematik, aber ab Ende der 50er Jahre wandte er sich den mathematischen Methoden der theoretischen Physik zu und publizierte zu Kosmologie, Relativitätstheorie und Quantenphysik. Penrose arbeitete eng mit Stephen Hawking zusammen. Für seine Arbeiten zum Zusammenspiel von Relativitätstheorie und Schwarzen Löchern erhielt er 2020 den Nobelpreis in Physik. Er ist der erste Nobelpreisträger in dieser Briefmarkenreihe, der zum Zeitpunkt der Veröffentlichung des Beitrags noch lebt.

Wir wollen hier Penroses mathematische Arbeiten in der theoretischen Physik nicht weiter besprechen; mit der rechten Briefmarke soll eine seiner rein geometrischen Entdeckungen vorgestellt werden, die auch für diejenigen verständlich ist, die keine professionellen Mathematiker sind. Penrose hat mehrere aperiodische Parkettierungen gefunden, die sowohl von mathematischem Interesse sind als auch von hohem ästhetischen Reiz.

Unter einer Parkettierung soll hier nur der einfachste Fall verstanden werden: Eine lückenlose und überschneidungsfreie Überdeckung der Ebene mit "Kacheln", die nur endlich viele verschiedene Formen annehmen können. Mehrere schöne Beispiele dafür findet man z.B. auf der zugehörigen Wikipedia-Seite. Eine Parkettierung heißt periodisch, wenn sich das Kachelmuster bei Verschiebungen in zwei verschiedenen Richtungen wiederholt. Dafür gibt es zahlreiche und kunstvolle Beispiele, z.B. diese:

       

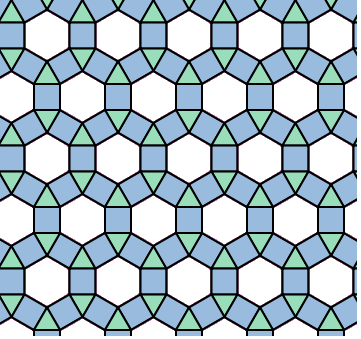
Bild 1      Links: Parkett aus gleichseitigen Drei-, Vier- und Sechsecken      Rechts: Mosaik aus der Alhambra in Granada

Aperiodische Parkettierungen haben diese Verschiebungseigenschaft nicht; außerdem enthalten sie keine beliebig großen periodischen Ausschnitte. Die besten bekannten Beispiele dafür wurden von Roger Penrose gefunden. Seine Parkettierung P3 enthält nur zwei verschiedene Typen von Rauten, die alle die gleiche Seitenlänge aufweisen und deren Zusammenfügung bestimmten Regeln unterliegt:



Bild 2      Penrose-Parkettierung P3

Im P3-Parkett  -  siehe Bild 2  -  hat die dünne Raute (grün) die Winkel 36° und 144° und die dicke Raute (blau) die Winkel 72° und 108°.

Die rechte Briefmarke stammt aus einem Satz, mit dem Macao den Goldenen Schnitt (port. A Proporção Dourada) würdigt. Dieser und die damit zusammenhängenden Fibonacci-Zahlen sowie die Goldene Zahl waren schon mehrfach Thema dieser Website, siehe die zugehörige Kategorie. Die Goldene Zahl  Φ =(1 + √5)/2 ≈ 1,618  findet sich auch in der Penrose-Parkettierung P3: Setzt man die Seitenlänge der Rauten  = 1 ,  so hat die lange Diagonale der dicken Raute die Länge  Φ  und die kurze Diagonale der dünnen Raute die Länge  1/Φ = Φ - 1 ≈ 0,618 .  Auch das Verhältnis der Flächeninhalte der dicken und dünnen Kacheln ist gleich  Φ .

Auf der Briefmarke ist eine andere Parkettierung zu sehen (port. Ladrilhos de Penrose = "Kacheln von Penrose"), die Penrose-Parkettierung P2:



Bild 3      Penrose-Parkettierung P2

P2 enthält ebenfalls nur zwei Polygone, die nach bestimmten Regeln zusammengefügt werden. Die Polygone heißen Pfeil und Drachen und sind in Bild 4 zu sehen:


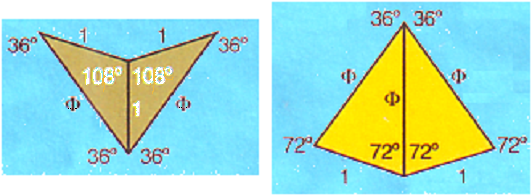
Bild 4      Pfeil und Drachen in P2

Der Pfeil hat die Winkel  36°, 72°, 36°, 216°  und der Drachen die Winkel  72° (dreifach),  144°.

Diese Winkel entstehen, indem die Polygone in je zwei gleiche Dreiecke mit den Seitenlängen  1, 1, Φ  bzw.  1, Φ, Φ  geteilt werden. Dies ist leicht zu zeigen:

Das Dreieck im Pfeil ist gleichschenklig und lässt sich in zwei rechtwinklige Dreiecke zerlegen. Damit ergibt sich für den spitzen Winkel  α :

cos α = Φ/2 = (1 + √5)/4   ⇒   α = 36°

Das Dreieck im Drachen ist ebenfalls gleichschenklig und lässt sich in zwei rechtwinklige Dreiecke zerlegen. Damit ergibt sich für den größeren Winkel  β :

sec β = 2·Φ = 1 + √5   ⇒   β = 72°

Bei den Parkettierungen P2 und P3 muss zur Vermeidung der Periodizität beachtet werden, dass die Kacheln nicht beliebig aneinandergefügt werden dürfen. Ausbuchtungen und Einkerbungen an den Kacheln (wie bei Puzzleteilen, siehe Bild 5) stellen das korrekte Zusammenfügen sicher. Insbesondere wird dadurch verhindert , dass in P3 zwei gleiche Kacheln bzw. in P2 zwei verschiedene Kacheln zu einem Parallelogramm zusammengefügt werden (dies allein ist aber nicht ausreichend zur Verhinderung einer periodischen Parkettierung). Bei der Darstellung der Penrose-Parkettierungen verzichtet man meist auf die Ausführung der Ausbuchtungen und Einkerbungen (die man sich ja auch als beliebig klein vorstellen kann).



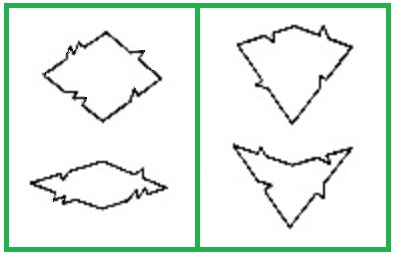
Bild 5      Fügeregeln für P3 und P2


Eine weiteres Objekt, das Roger Penrose gefunden hat: Penrose-Dreieck


Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge

Publiziert 2021-09-13          Stand 2020-12-20