

Italien 2018 Michel 4030 Vatikan 2018 Michel 1938
Mathematikerinnen
Folge 2
Maria Gaetana Agnesi (1718 - 1799)
In früheren Zeiten, und teilweise bis heute, war es für Frauen schwer oder unmöglich, eine wissenschaftliche Laufbahn einzuschlagen. Dies gilt auch für die Mathematik. Es ist aber anzunehmen, dass sich mathematisches Talent bei Frauen etwas leichter entfalten konnte als eine naturwissenschaftliche Begabung, da letztere in der Regel einen Zugang zu Laboren benötigt, der Frauen vielfach verwehrt blieb. Mathematik lässt sich auch im Stillen ausüben. Viel schwerer ist es allerdings, eine öffentliche Wirkung eigener Forschung zu entfalten; das zeigen einige der hier vorgestellten Lebensläufe von Mathematikerinnen auf. In jüngerer Zeit findet man aber zunehmend erfolgreiche akademische Karrieren von Mathematikerinnen; einige von ihnen werden mit Briefmarken in dieser Reihe geehrt.
Der Begriff der "Mathematikerin" soll hier nicht allzu eng gefasst werden. Der Bezug der Frauen in dieser Reihe zur Mathematik ist mal mehr und mal weniger ausgeprägt und manchmal nur durch die Anwendung der Mathematik in anderen Gebieten bestimmt.
Die Reihe wird in unregelmäßigen Abständen weitergeführt werden.
|
frühere Beiträge:
→ Folge 1 Maria Mitchell
weitere Beiträge siehe Liste (farbcodiert)
In Mathematische Philatelie: Maria do Pilar Ribeiro
Eintrag bei Marke # 119 (ohne Bild): Hilda Phoebe Hudson
|
Die beiden gezeigten Briefmarken wurden anlässlich des 300. Geburtstags von Maria Agnesi ausgegeben.
Die italienische Mathematikerin Maria Agnesi stand im Ruf eines Wunderkinds, da sie schon in sehr jungen Jahren Mathematik und zahlreiche Fremdsprachen beherrschte. Ihre wohlhabende Mailänder Familie ermöglichte ihr Hausunterricht durch namhafte Gelehrte. Offenbar besuchte sie niemals eine Schule oder Hochschule. Bis zum Alter von 30 Jahren wirkte sie als Privatgelehrte. 1748 erlebte sie den Höhepunkt ihres wissenschaftlichen Lebens. In diesem Jahr erschien ihr Werk Instituzioni Analitiche, und bald darauf wurde sie auf den Lehrstuhl für Mathematik der Universität Bologna berufen.
Damit war sie die erste Frau, die als Autorin eines Lehrbuchs für Mathematik hervortrat, und sie war die erste Mathematikprofessorin an einer Universität.
Gelehrt an der Universität Bologna hat Maria Agnesi nicht. Ihre Berufung dorthin hat sie aber auf der Titelseite der Instituzioni Analitiche bekanntgegeben (Bild 1). Bis 1752 hat sie noch mathematische Forschung betrieben und gab dann die Wissenschaft zugunsten ihrer Religion und karitativem Wirken auf. Sie studierte Katholische Theologie und betreute Arme und Kranke. Ab 1771 leitete sie ein Altenheim für Frauen. Sie wendete ihr gesamtes Vermögen für wohltätige Zwecke auf.
Instituzioni Analitiche
Maria Agnesi verfasste dieses zweibändige Lehrbuch zur Unterrichtung der italienischen Jugend. Es enthält eine systematische Abhandlung der Differential- und Integralrechnung. Der heutige Leser ist beeindruckt von den zahlreichen und ausführlich erläuterten Beispielen und den detaillierten Illustrationen. Die Instituzioni Analitiche enthalten an mehreren Stellen Ausführungen zu der Kurve, die nach Maria Agnesi benannt wurde, der Versiera der Agnesi.
Die Versiera der Agnesi
Die italienische Briefmarke zeigt die Versiera unter Agnesis Portrait. Die Skizze enthält auch die wesentlichen Elemente der Konstruktion der Versiera als Ortskurve. Eine ähnliche Skizze sieht man auf der Vatikan-Marke auf dem Boden liegen. Diese Briefmarke enthält außerdem eine Gleichung aus der Beweisführung (unterhalb des Betstuhls) und die Funktionsgleichung für einen Spezialfall der Versiera (an der Wand).
Die Versiera hatten vor Maria Agnesi schon andere Mathematiker beschrieben; sie wurde nach ihr benannt, weil sie sie in ihrem weit verbreiteten Lehrbuch Instituzioni der Öffentlichkeit zugänglich gemacht und einer ausführlichen Untersuchung unterworfen hat.
Maria Agnesi hat in den Instituzioni die Versiera nicht in der Form angegeben, wie es in heutigen Lehrbüchern üblich ist. In diesen findet man meist die folgenden Definitionen:
a) Geometrische Konstruktion als Ortskurve
b) Explizite Gleichung y = f(x)
c) Parametergleichung g(α) = (x(α), y(α))
In den Instituzioni finden wir zunächst die Ortskurve, aus deren Eigenschaften dann eine explizite Gleichung hergeleitet wird (Bild 2). Diese hat allerdings eine andere Orientierung als üblich: Agnesi wählt die senkrechte Achse als x-Achse und die waagerechte als y-Achse und berechnet y = h(x); somit ist h = f-1 ; die heute übliche Funktion f aus b) findet sich nicht in den Instituzioni. Wir wollen nun Definition und Herleitung aus dem Buch der Agnesi (Bild 2) rekonstruieren.

Bild 2
Die Ortskurve der Versiera entsteht mit Hilfe eines Kreises mit Durchmesser AC wie in Fig. 135 in Bild 2. (AC usw. wird im Folgenden sowohl für die Strecke als auch für deren Länge verwendet, dem jeweiligen Zusammenhang entsprechend.) Auf dem Kreis wird ein beliebiger weiterer Punkt D gewählt. Das Lot von D auf AC habe den Fußpunkt B ; es wird außerhalb des Kreises verlängert bis zum Punkt M , sodass AB/BD = AC/BM gilt. M ist dann ein Kurvenpunkt der Versiera. Man beachte, dass in Fig. 135 BM = CE gilt; damit wird das Streckenverhältnis zu AB/BD = AC/CE (ähnliche Dreiecke ADB und AEC ). Die ganze Kurve erhält man, indem D sämtliche Kreispunkte durchläuft.
Genau genommen gilt diese Konstruktion für D ≠ A und D ≠ C . C wird zusätzlich als Kurvenpunkt hinzugenommen.
Auf der Briefmarke des Vatikans sieht man unterhalb der Kirchenbank das Verhältnis der Streckenlängen in der Darstellung der Instituzioni : AB,BD::AC,BM (vergrößert in Bild 3; auch enthalten in Bild 2).

Bild 3
Eine ähnliche und äquivalente Konstruktion der Ortskurve erhält man mit Hilfe eines Kreises mit Durchmesser AC und der Tangente in C . Von A wird eine beliebige Sekante durch den Kreis gelegt, die den Kreis in D und die Tangente in E schneidet. Das Lot von D auf AC habe den Fußpunkt B . Vervollständigt man nun BEC zum Rechteck BMEC , so ist M ein Kurvenpunkt der Versiera. Die ganze Kurve erhält man, indem AD sämtliche Sekanten durch A durchläuft.
Nach der Definition der Ortskurve führt Maria Agnesi Koordinaten für M ein, indem sie x = AB und y = BM setzt, um zu einer Funktionsgleichung y = h(x) in einem rechtwinkligen Koordinatensytem mit Ursprung in A zu gelangen. Sie setzt a = AC und erhält mit dem Höhensatz:
(1) (BD)2 = x(a-x)
Aus der Konstruktion der Ortskurve ist bekannt: AB/BD = AC/BM . Also gilt:
(2) x/BD = a/y
Aus (1) und (2) folgt für y ≥ 0 :
Das ist die Versiera, wie sie von Maria Agnesi publiziert wurde (siehe Bild 2, S. 381, erster Absatz). In dieser Form findet man sie heute kaum noch. - Die vollständige Kurve erhält man, wenn auch y = -a((a-x)/x)1/2 zugelassen wird; diese Lösung ergibt sich ebenfalls aus (1). - x durchläuft das Intervall (0,a] auf der senkrechten Achse und y alle reellen Zahlen auf der waagerechten Achse.
Schreibt man y = h(x) = ± a((a/x - 1)1/2 , erhält man x = a3/(y2 + a2) und nach Variablentausch die Umkehrfunktion
(3) y = f(x) = a3/(x2 + a2)
Dies ist die heute verbreitete Funktion zur Darstellung der Versiera. Hier sind x und y in üblicher Ausrichtung gewählt: x auf der waagerechten, y auf der senkrechten Achse. Wählt man a = 6 , so ist y = 216/(x2 + 36); dies lässt sich umformen zu der Funktion, die man an der Wand auf der Vatikan-Marke sieht:
(4) y = 8·33/(x2 + 4·32)
(4) entspricht einer anderen gängigen Funktion der Versiera, die statt des Kreisdurchmessers a den Radius r verwendet:
y = 8·r3/(x2 + 4·r2)
An anderer Stelle der Instituzioni berechnet Agnesi die Wendepunkte der Kurve (Bild 4). Dies gelingt leicht durch zweifaches Ableiten von (3) bzw. (4); man erhält die Punkte (± a/√3 , a·3/4).

Bild 4
Eine Parameterdarstellung wie in c) hat Maria Agnesi nicht angegeben, aber sie lässt sich leicht aus der Konstruktion der Ortskurve herleiten (Bild 5).
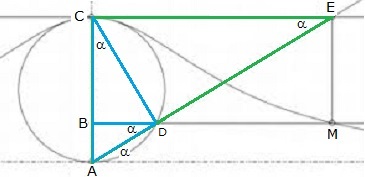
Bild 5
Bild 5 entspricht der Darstellung in den Instituzioni (Fig. 135 in Bild 2). Als Winkel α für die Parameterdarstellung soll der Winkel zwischen der positiven Richtung der waagerechten Achse und AD gewählt werden; α kommt in Bild 5 noch an drei weiteren Stellen vor. Für die Koordinaten des Kurvenpunktes M setzen wir x = BM = CE und y = AB ; außerdem sei wieder a = AC . Dann ist x = a cot α (Dreieck AEC). y ermittelt man aus sin α = AD/a (Dreieck ADC) und sin α = y/AD (Dreieck ADB) zu y = a sin2 α . Damit erhalten wir die Parameterdarstellung der Versiera:
(5) g(α) = (x(α), y(α)) = (a cot α , a sin2 α)
Diese Parameterdarstellung gilt auch für den 2. Quadranten, also für α ∈ [π/2,π). Dies folgt aus cot(π/2 + γ) = -cot(π/2 - γ) und sin(π/2 + γ) = sin(π/2 - γ).
y(α) lässt sich auch analytisch aus (3) herleiten:
x = a cot α ⇒ y = a/(cot2 α + 1) = a sin2 α/(cos2 α + sin2 α) = a sin2 α
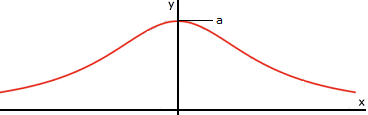
Eine Stammfunktion von (3) ist F(x)= a2·arctan(x/a). Damit erhält man π·a2 als Flächeninhalt zwischen Kurve und waagerechter Achse. Somit ist P(x)= f(x)/(π·a2)= a/(π(x2 + a2)) eine Wahrscheinlichkeitsverteilung, die als zentrierte Cauchy-Verteilung bekannt ist.
Außer den gezeigten Briefmarken gibt es noch weitere philatelistische Belege zu Maria Agnesi. Bild 6 zeigt eine individuell gestaltete Marke aus den USA:

Bild 6
Es gibt mehrere Postkarten mit Maria Agnesis Portrait; davon werden in Bild 7 zwei sehr alte und seltene gezeigt. Die Karte links mit dem Stempel des Circolo Gaetana Agnesi Milano ist von beiden Seiten zu sehen und stammt laut Ankunftsstempel in Vicenza aus dem Jahr 1900. Die zweite Karte wurde in 100 Exemplaren zum 100. Todestag Maria Agnesis ausgegeben; gezeigt wird die noch gut erhaltene postfrische # 71, die auf Auktionen ca. 200 Euro erzielt.


Bild 7 Briefmarken: Italien 1896 Michel 67 Scott 68 Italien 1879 Michel 38 Scott 46
Publiziert 2021-04-26 Stand 2019-09-01
vorige Marke | Liste aller Briefmarken | nächste Marke | Mathematische Philatelie
Manfred Börgens | zur Leitseite












