 MB Matheblog # 22
MB Matheblog # 22voriger Eintrag nächster Eintrag
Index der gesamten Website
 MB Matheblog # 22 MB Matheblog # 22 |
Inhalt Blog voriger Eintrag nächster Eintrag |
zur Leitseite Index der gesamten Website |



|
Die Hirtensonnenuhr im Vergleich zu anderen Sonnenuhren
In den letzten vier Blogbeiträgen wurden verschiedene Beispiele von Sonnenuhren vorgestellt. Zusammen mit der Hirtensonnenuhr fallen sie im Wesentlichen in zwei Typen. Die äquatorialen Sonnenuhren und der Gnomon (Teil 1, Teil 2, Teil 4) verwenden die Himmelsrichtung der Sonne für die Ablesung der Uhrzeit; außerdem bieten sie die Möglichkeit, über die Schattenlänge auch das Datum abzulesen (Teil 2, Teil 4). Der zweite Typ wird hier durch die Aquitaine (Teil 3) und die Hirtensonnenuhr repräsentiert. Diese verwenden den Höhenwinkel der Sonne für die Ablesung der Uhrzeit. Der Vergleich der fünf Uhren ist in der folgenden Tabelle dargestellt. |
| Uhrzeit | Datum (über Deklination) | Zeitgleichung | Was muss bekannt sein? | ||
| Teil 1 | äquatorial (Eigenbau) | Richtung der Sonne | – | – | Nordrichtung + Breite (variabel) |
| Teil 2 | äquatorial + analemmatisch | Richtung der Sonne | Höhenwinkel der Sonne | + | Nordrichtung + Breite (variabel) |
| Teil 3 | Aquitaine-Ringsonnenuhr | Höhenwinkel der Sonne | – | – | Datum + Breite (fest) |
| Teil 4 | Gnomon | Richtung der Sonne | Höhenwinkel der Sonne | – | Nordrichtung + Breite (fest) |
| Teil 5 | Hirtensonnenuhr, zylindrisch | Höhenwinkel der Sonne | – | – | Datum + Breite (fest) |
|
Berechnung der Schattenlinien auf der Sonnenuhr
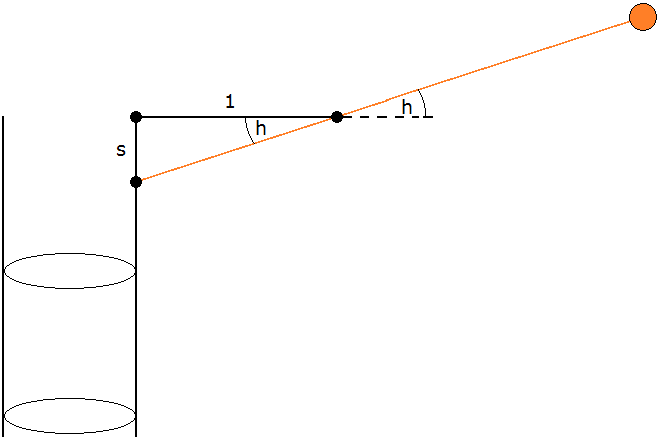
\(h~\): Höhenwinkel der Sonne über dem Horizont, siehe Bild 2 \(s~\): Länge des Schattens auf der Sonnenuhr, siehe Bild 2 \(\phi~\): Breitengrad des Beobachters \(\delta~\): Deklination der Sonne \(t~\): Tages-Nr. im Jahr \(\tau~\): Uhrzeit, im Text angegeben in Stunden und Minuten, in den Formeln in Grad (\(~0° = 00:00~\text{Uhr},~~90° = 06:00~\text{Uhr}~\) usw.) Wir setzen \(~y~\) als Abkürzung für \(~\text{sin}~h~\) in Bild 2. \(\textbf{(1)}~~y=\text{sin}~h = -\text{cos}~\delta~\text{cos}~\tau~\text{cos}~\phi + \text{sin}~\delta~\text{sin}~\phi\) Die rechte Seite der Gleichung ↑ findet man in der Geo-astronomischen Formelsammlung auf dieser Website als Formel (8). \(\textbf{(2)}~~\delta = 0,4095~\text{sin}\left(0,016906~(t - 80,086)\right)\) Näherungsformel, etwas ungenau zu Sommer- und Winteranfang; siehe Quelle [1] In Bild 2 ist \(~s=tan~h~\). \[s = \text{tan}~h = \frac{\text{sin}~h}{\sqrt{1-\text{sin}^2~h}} = \frac{1}{\sqrt{\left(\text{sin}^{-2}~h\right)-1}}\] \[\textbf{(3)}~~s = \left(y^{-2}-1\right)^{-\frac{1}{2}}\] Damit ist \(~s~\) nach (1), (2) eine Funktion des Beobachter-Breitengrads \(~\phi~\), des Datums \(~t~\) und der Uhrzeit \(~\tau~\). Ist die Deklination der Sonne bekannt (z.B. aus der Messung der Mittagshöhe oder aus einer Tabelle), kann man natürlich auf (2) verzichten. Mit \(~s~\) zeichnet man die Schattenlinien auf der Sonnenuhr. \(~\phi~\) ist dabei fest; feste \(~\tau~\) werden im Stundenabstand gesetzt; also ist \(~s~\) für jede der Kurven auf der Sonnenuhr eine Funktion des Datums \(~t~\) bzw. der Deklination \(~\delta~\). Die Berechnungen für die Stundenlinien auf der Hirtensonnenuhr unterliegen den gleichen theoretischen Beschränkungen wie in der Geo-astronomischen Formelsammlung (siehe dort die Hinweise zur "Idealisierung" am Ende der Ausführungen zum geozentrischen Modell hinter (1) sowie Beispiel 7). Insbesondere gilt das für die noch folgenden Beispiele; die dort angegebene Genauigkeit ist für praktische Belange ohne Bedeutung. Für Hermanns Sonnenuhr spielt das schon deshalb keine Rolle, weil die Monats- und Stundeneinteilungen keine hohe Genauigkeit zulassen. |
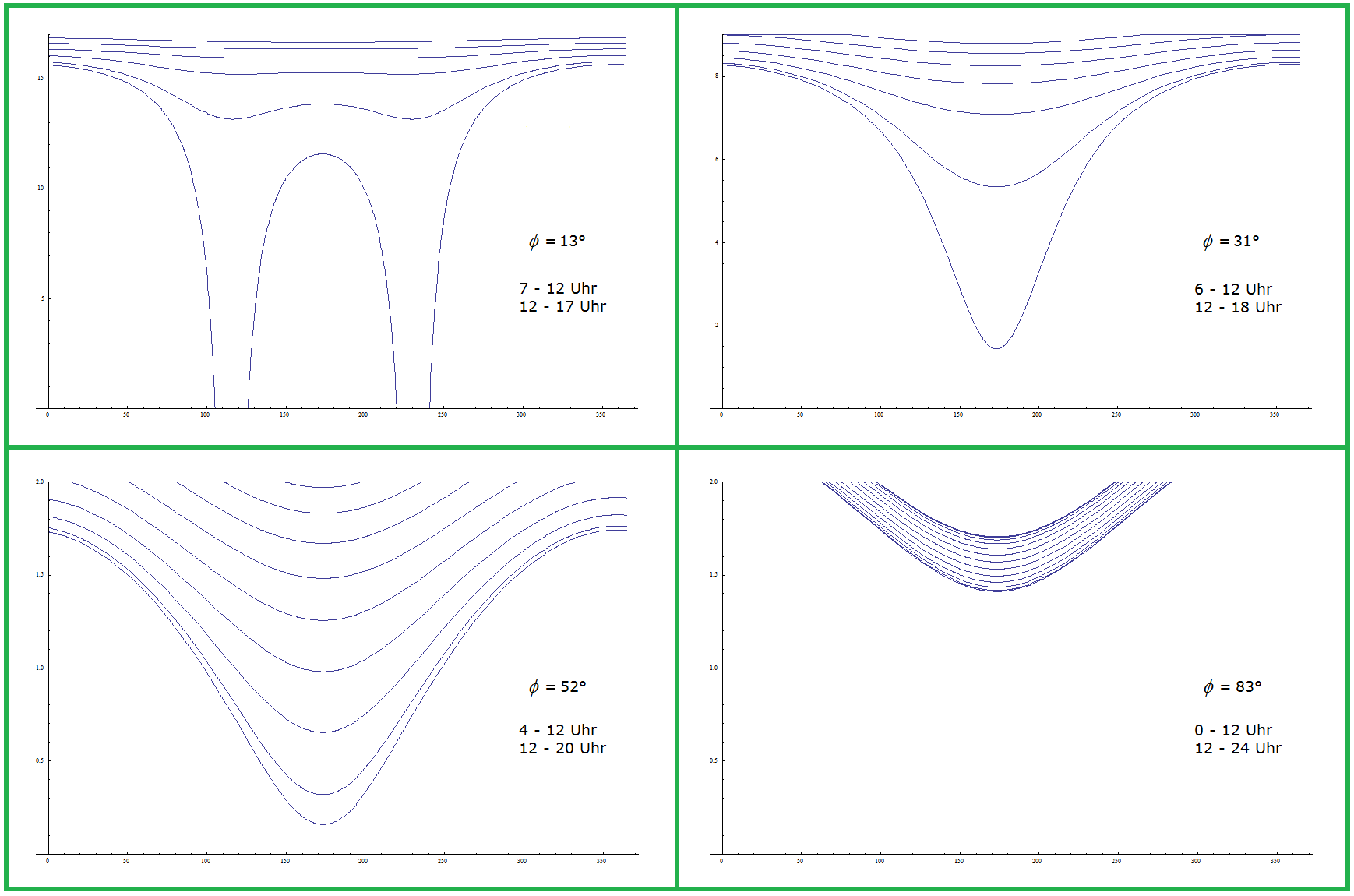
Umrechnung von Sonnenzeit auf bürgerliche Zeit
|
|
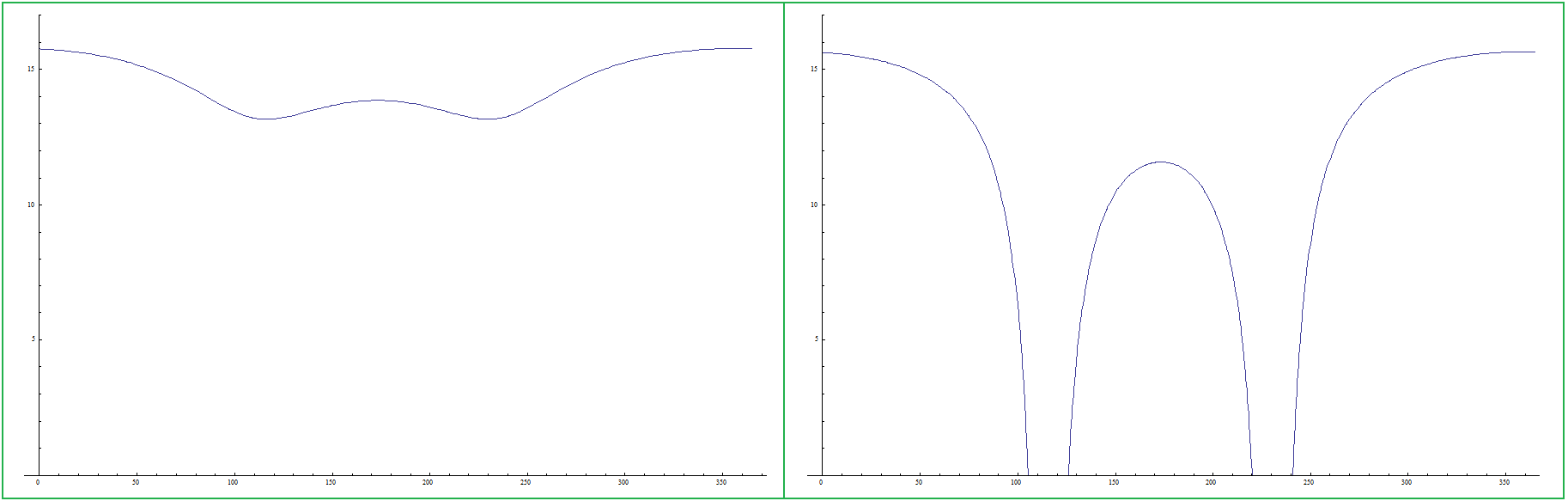
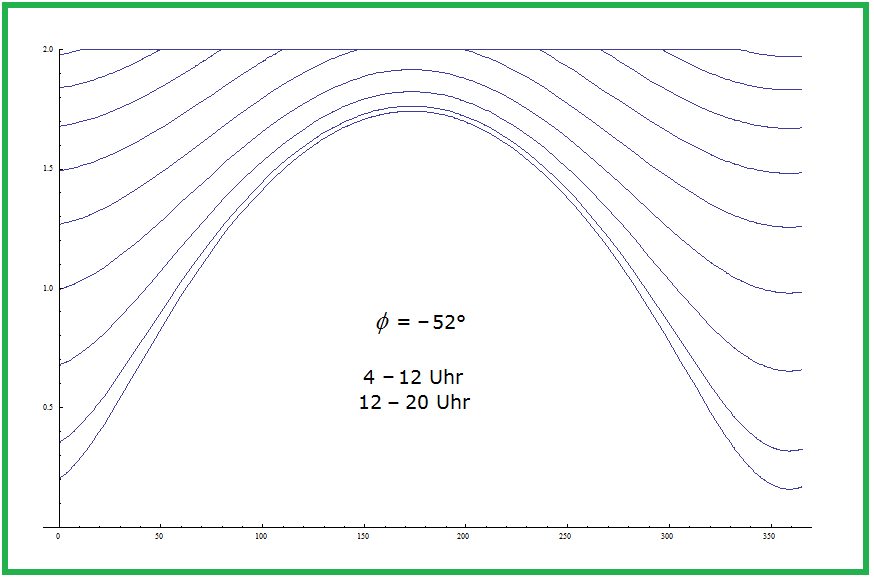
Wie könnte man eine analemmatische Hirtensonnenuhr mit Anzeige der bürgerlichen Zeit anfertigen? Theoretisch: Kein Problem. Praktisch: Eher schwierig. Die Längengradkorrektur ist problemlos. Man muss dafür nur die Uhrzeitkurven auf der Sonnenuhr anders beschriften. Befindet man sich z.B. auf \(~7,5°\) östlicher Länge und möchte die \(9\text{-Uhr-}\)Kurve zeichnen, so wählt man in (1) \(~\tau = 08:30~\). Die unterste Kurve, die man zeichnen kann (Mittagskurve für \(~\tau = 12:00~\)) erhält dann die Beschriftung \(~12:30~\), darüber würde die Kurve für \(~\tau = 11:30~\) und \(~\tau = 12:30~\) mit der Beschriftung \(~12:00~\) und \(~13:00~\) liegen. Auch die Sommerzeit lässt sich bequem eintragen. In dem entsprechenden Tagesintervall werden die Beschriftungen um eine Stunde erhöht. Für eine analemmatische Sonnenuhr (siehe Teil 2) bleibt noch die Zeitgleichung zu berücksichtigen, die wir in Abhängigkeit von \(~t~\) gemäß Quelle [1] wie \(~\tau~\) in Grad messen: \[z = (-0,171~\text{sin}~(0,0337~t + 0,465) - 0,1299~\text{sin}~(0,01787~t - 0,168))\cdot 15°\] In (1) nimmt man die folgenden Korrekturen vor: \(\tau~~\rightarrow~~\tau + z~~\) vormittags \(\tau~~\rightarrow~~\tau - z~~\) nachmittags Hier setzen die praktischen Schwierigkeiten ein. Die ursprünglichen Stundenlinien werden jeweils durch zwei andere ersetzt, die zudem noch nah beisammenliegen und die Ablesung erschweren. Dazu schaue man sich die Bilder 6 und 7 an. Die schwarzen Kurven stammen von der ursprünglichen Sonnenuhr und sind identisch, da sie symmetrisch zu \(~12:00~\text{Uhr}~\) liegen. Ohne Berücksichtigung der Zeitgleichung würden diese Kurven einfach mit \(~09:00/15:30~\) außerhalb der Sommerzeit und \(~10:00/16:30~\) während der Sommerzeit beschriftet. Die grünen Kurven stehen für eine analemmatische Sonnenuhr; legte man die Bilder 6 und 7 übereinander, so lägen diese Kurven sehr nahe beieinander. 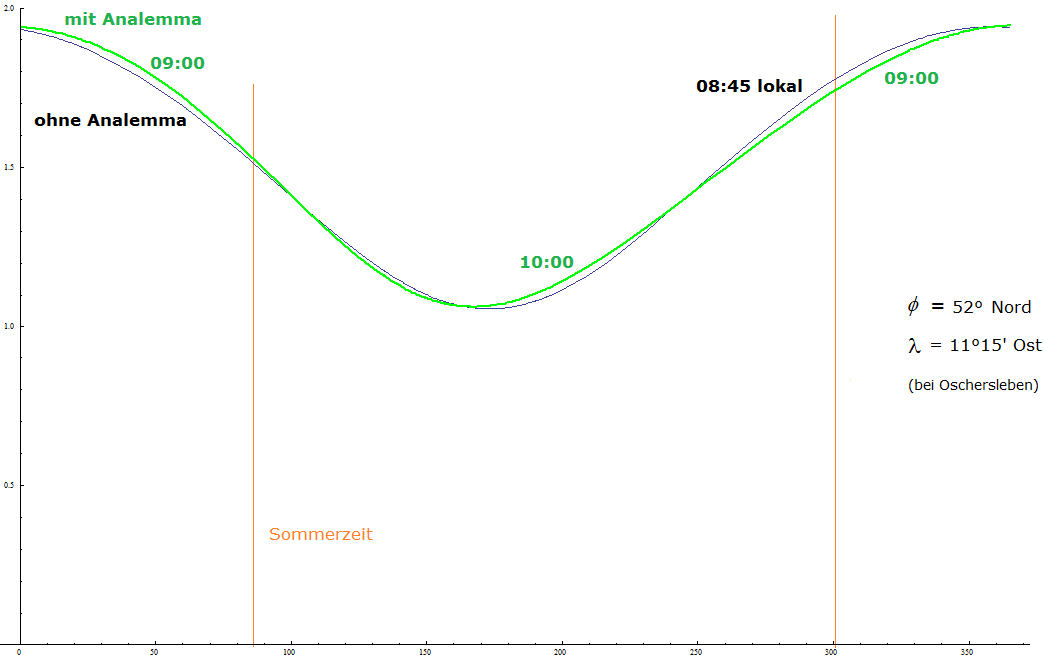
Bild 6 Analemma vormittags 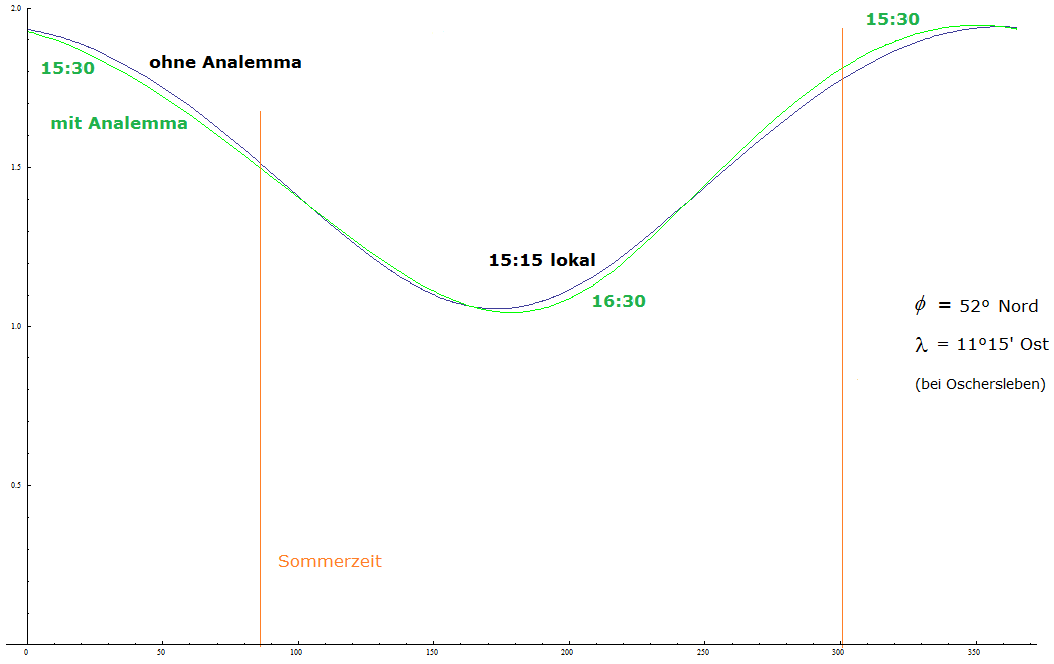
Bild 7 Analemma nachmittags Wenn man Hermanns Sonnenuhr genügend groß macht (etwa wie eine Litfaßsäule – das wäre eine schöne Idee), ist eine analemmatische Version möglich. Für die Uhrzeitkurven in Bild 3, die eng zusammenliegen, vor allem in den oberen Bereichen (kurze Schatten) und für die Polarregion, könnte man den Effekt der Zeitgleichung allerdings kaum erkennen. Beim Wechsel von vormittags zu nachmittags entlang der \(12\text{-Uhr-}\)Linie verhält es sich ebenso; die schwarzen und grünen Kurven liegen so nah beieinander, dass das Analemma ohne praktische Bedeutung ist. Das ist leicht erklärbar: Wenn die Sonne im Zenit steht, hat sie für einige Minuten vorher und nachher – auch in der Größenordnung der Zeitgleichung – in etwa den gleichen Höhenwinkel \(~h~\) in (1). Fazit: Man kann leicht eine Hirtensonnenuhr mit Längengradkorrektur und Sommerzeit fertigen, aber eine analemmatische Variante würde einen großen Zylinder (für Hirten nicht zu bewegen) erfordern und auch dann nur für einen Teil der Uhrzeitkurven ablesbar sein. |
Stand 2022-02-10
Inhalt Blog | voriger Eintrag | nächster Eintrag