Dodekaeder    MB Matheblog # 23 Inhalt Blog
voriger Eintrag    nächster Eintrag		 zur Leitseite
Index der gesamten Website


2022-12-06                                                                 Kommentare sind willkommen.


Bestimmung des Breitengrads aus der Tageslänge


In der Rubrik  Mathematische Probleme  auf dieser Website wurde kürzlich im Problem # 120 eine geo-mathematische Frage diskutiert, die auf einen Beitrag im Riddler Express zurückgeht. Hier im Blog wird das Problem nochmal aufgegriffen und ergänzt; das Augenmerk soll auf den folgenden Kern der Argumentation gelegt werden:

Ein Beobachter misst an einem bestimmten (bekannten) Datum den zeitlichen Abstand zwischen Sonnenauf- und untergang. Kann er daraus die geographische Breite seines Standorts bestimmen ?

Ja  –  theoretisch geht das auf jeden Fall (falls nicht zufällig das Datum auf eines der Äquinoktien fällt).

Aber: Die praktische Durchführung zeigt, dass erhebliche Ungenauigkeiten zu erwarten sind.

Dennoch: Zur Auffindung einer Insel im Ozean  –  so wie im Riddler Express oder im Problem # 120 beschrieben  –  kann sich die theoretische Berechnung des Breitengrads, mit einiger Umsicht angewandt, durchaus eignen.

Natürlich muss dafür auch die geographische Länge der Insel bekannt sein. Auf der Problemseite wurde gezeigt, dass dies nur von geringem mathematischem Interesse ist. Man benötigt lediglich eine Uhr, von der man weiß, in welcher Zeitzone man sie eingestellt hat. Die Bestimmung der geographischen Breite dagegen erfordert geo-mathematische Kenntnisse; deshalb beschränken wir uns hier darauf.

Die Grundidee ist einfach und naheliegend. In Bild 1 sieht man, wie eine Hälfte der Erdkugel von der Sonne beschienen wird. Der Nordpol liegt im Dunkeln, also wurde hier beispielhaft ein Wintertag auf der Nordhalbkugel für die Darstellung gewählt. Je weiter nördlich die geographische Breite liegt, desto geringer ist der beleuchtete Anteil. Dieser Anteil entspricht der "Tageslänge"  –  so wollen wir die Zeit zwischen Sonnenauf- und untergang nennen. Es besteht also offenbar ein eindeutiger Zusammenhang zwischen dem Breitengrad und der Tageslänge, siehe die gelben Linien in Bild 1.  –  Aber Vorsicht: Es gibt eine Ausnahme. An den Äquinoktien, also zu Frühlings- und Herbstanfang, geht in Bild 1 die Schattenlinie durch die Pole, also beträgt die Tageslänge überall auf der Erde  12 Stunden .  –  Im Polarwinter (dunkle Kugelkappe am Nordpol in Bild 1) und im Polarsommer (helle Kugelkappe am Südpol in Bild 1) gibt es keinen Sonnenauf- oder untergang; die entsprechenden Breiten spielen also für unsere Problemstellung keine Rolle.

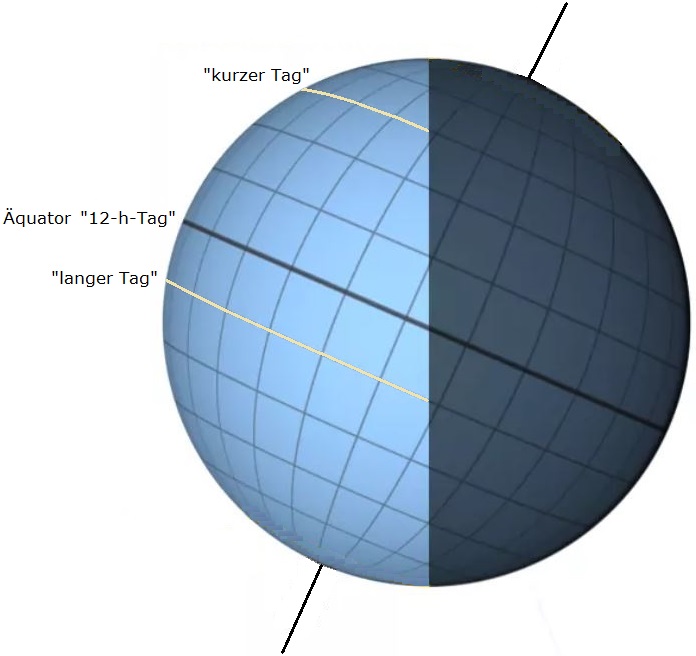
Tageslängen im Winter
Bild 1
Unterschiedliche Tageslängen an einem Wintertag auf der Nordhalbkugel


Geo-astronomische Koordinaten

Zur Beschreibung und Berechnung der Position eines Gestirns am Himmel verwendet man astronomische Koordinatensysteme, die in der Geo-astronomischen Formelsammlung auf dieser Website an den Sonnenlauf angepasst wurden. Dort wurde der Azimut äquivalent als Himmelsrichtung beschrieben. So erhält man für die Koordinaten fünf Variablen:
  •  Äquatoriale Koordinaten
     –   δ   Deklination
     –   τ   Uhrzeit (in Grad gemessen)

  •  Horizontale Koordinaten
     –   h   Höhenwinkel
     –   A   Himmelsrichtung (in Grad gemessen)

  •  φ   Geographische Breite des Beobachters
Mit  φ  lassen sich die äquatorialen in horizontale Koordinaten umrechnen und umgekehrt. Die Umrechnungsformeln findet man in der Formelsammlung. Sie zeigen, dass zur Berechnung einer der fünf Variablen drei der restlichen vier beobachtet werden müssen.

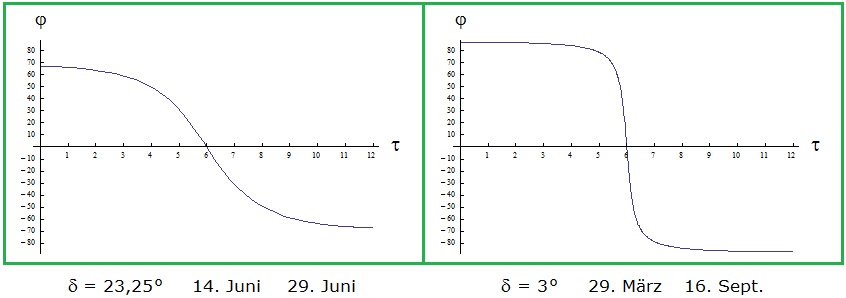
Bei unserem Inselproblem sind  h = 0°, τ  und  δ  bekannt.

τ  steht für die Ortszeit des Betrachters zu Sonnenaufgang und ergibt sich leicht aus der gemessenen Tageslänge: Der Abstand von  τ  zu  180° (= 12 Uhr mittags) ist die halbe Tageslänge.  –  δ  ergibt sich aus dem Datum mit Hilfe einer Formel (siehe (4) in Blog # 19) oder einer Tabelle.

Mit (52) in der Formelsammlung erhalten wir die gesuchte geographische Breite  φ :
φ = arctan(cot δ cos τ)


Es gibt mehrere mögliche Quellen für Fehler und Abweichungen:

In den Modellrechnungen auf der Problemseite wird von  10''  Ungenauigkeit ausgegangen, aber das könnten durchaus auch deutlich mehr sein. Abweichungen von  50 km  und mehr in Nord-Süd-Richtung können auftreten, wenn man sich den Äquinoktien nähert. Da in Problem # 120 gezeigt wurde, dass sich die geographische Länge recht genau bestimmen lässt, kann das aber immer noch insgesamt ausreichen, um die Insel zu finden.



Kategorie: Geomathematik                    Kommentare sind willkommen.


Stand 2022-04-03

Inhalt Blog   |    voriger Eintrag   |    nächster Eintrag

Manfred Börgens   |   Zur Leitseite