Manfred Boergens - Geo-astronomische Formelsammlung

zur Leitseite Index der gesamten Website

Geo-astronomische Formelsammlung Kommentare sind willkommen: E-Mail

Diese Formelsammlung dient der Beschreibung geozentrischer Koordinatensysteme. Teile davon sind schon mehrfach auf dieser Website verwendet worden. Hier soll ein zusammenhängender Überblick gegeben werden, der als Basis weiterer Beiträge über Mathematische Probleme, Mathematik auf Briefmarken und in diesem Blog dienen soll. Wir greifen zunächst zurück auf einen großen Abschnitt aus Blog # 3 und übernehmen von dort weitgehend die Ausführungen zu Kugelkoordinaten. Anschließend werden daraus Formeln für den Sonnenlauf hergeleitet.

Kugelkoordinaten haben keine einheitliche Definition, da die Orientierung der "Länge" und der "Breite" verschieden gewählt werden kann. In Bild 1 sehen wir zunächst die Standard-Variante, wie sie oft auch für die geographischen Koordinaten auf der Erde verwendet wird, wenn man von den leichten Abweichungen von der Kugelform absieht. Die Kugel ist leicht zum Betrachter hin geneigt; der schwarze Punkt ist der höchste Punkt der Kugel mit den Koordinaten \((x,y,z)=(0,0,r)\), mit \(~r~\) als Radius der Kugel. Die Länge \(~\beta \in [~0°,360°)~\) läuft im Gegenuhrzeigersinn um die Kugel, wenn man von der positiven \(z-\)Richtung auf die \(x-y-\)Ebene schaut; \(~0°\) liegt auf der positiven Richtung der \(x-\)Achse. Die Breite \(~\gamma \in [-90°,90°]~\) hat das gleiche Vorzeichen wie die \(z-\)Koordinate. – Der grüne Punkt auf der Kugeloberfläche in Bild 1 lässt sich also sowohl mit kartesischen Koordinaten \((x,y,z)\) als auch mit Kugelkoordinaten \((\gamma,\beta,r)\) beschreiben.

Bild 1 Kugelkoordinaten\(~(\gamma,~\beta)~\). \(~\gamma~\) ist die "Breite", \(~\beta~\) die "Länge". Die dritte Koordinate \(~r~\) wurde weggelassen, da sie im Folgenden immer als zu \(~1~\) normiert angenommen wird.

Eine einfache trigonometrische Herleitung führt für \(~r=1~\) auf die folgende Transformation:

Transformation Kugelkoordinaten → kartesische Koordinaten

\(\gamma~\) Breite, \(~\beta~\) Länge (Gegenuhrzeigersinn)
\begin{array}{ll} \textbf{(1)} & x = cos~\gamma~cos~\beta\\ ~ & y = cos~\gamma~sin~\beta\\ ~ & z = sin~\gamma \end{array}

Nun zum geozentrischen Modell und zur Himmelssphäre: Beide Begriffe sind Hilfsmittel zum Verständnis der relativen Bewegungen von Erde und Sonne. Im heliozentrischen Modell wird die Sonne als fixiert und zentral angenommen, und die Erde kreist innerhalb eines Jahres um die Sonne, was u.a. an den Jahreszeiten erkennbar ist. Der Wechsel von Tag und Nacht zeugt von der Eigenrotation der Erde. Vor der Verbreitung der heliozentrischen Weltsicht war das geozentrische Modell weithin anerkannt, in dem die Erde als fixiert und zentral angenommen wird und die Sonne täglich um die Erde kreist; die Jahreszeiten werden durch die im Jahresverlauf wechselnden Einfallswinkel der Sonnenstrahlen erklärt. Es ist gänzlich unwissenschaftlich, das heliozentrische Modell als richtig und modern und das geozentrische Modell als falsch und veraltet zu betrachten. Beide Modelle sind geometrisch äquivalent, eine Unterscheidung nach richtig und falsch ist nicht möglich. Das heliozentrische System ist erheblich besser geeignet, wenn man unser gesamtes Planetensystem einbezieht. Für viele Erscheinungen, die wir auf der Erde beobachten und die den Sonnenstand betreffen, ist jedoch das geozentrische Modell gut geeignet und sehr anschaulich.

Im geozentrischen Modell bewegt sich die Sonne auf einer Kugel, deren Mittelpunkt die Erde ist. Den Radius der Kugel wollen wir als zu \(~1~\) normiert annehmen. Da die Entfernung Erde - Sonne etwas schwankt, handelt es sich nicht um eine exakte Kugel, was aber bei der Beschreibung vieler geo-astronomischer Phänomene unerheblich ist. Außerdem ist die Erde im Verhältnis zum Radius der Kugel winzig, so dass sie bei Bedarf näherungsweise als punktförmig betrachtet werden kann. Die Kugel bezeichnen wir als Himmelssphäre. Die Position der Sonne auf der Himmelssphäre wird mit Kugelkoordinaten angegeben. Dafür geben wir zwei Koordinatensysteme als Varianten von (1) an: Das horizontale Koordinatensystem beschreibt den Sonnenstand aus Sicht eines irdischen Betrachters mit der Höhe über dem Horizont und der Himmelsrichtung der Sonne. Im äquatorialen Koordinatensystem wird der Sonnenstand mit Hilfe des Datums und der Uhrzeit angegeben. Wie geht der geographische Breitengrad des Beobachters in die Berechnungen ein? Dies ist gerade diejenige Variable, die die beiden Koordinatensysteme verbindet, insbesondere eine Koordinatentransformation zwischen den Systemen erlaubt.

Dass die folgenden Ausführungen unter leicht idealisierten Annahmen behandelt werden, wurde schon erwähnt. Im einzelnen betrifft das die folgenden Punkte:
    Erde kugelförmig
    Erdbahn kreisförmig
    Erdradius gegenüber Abstand Erde - Sonne vernachlässigbar klein
    kein Linseneffekt der Atmosphäre
        Die ersten drei Annahmen führen zu leichten Verzerrungen der Ergebnisse, die hier nicht berücksichtigt werden.
        Der Linseneffekt der Atmosphäre führt dazu, dass wir die Sonne bereits einige Minuten vor
        ihrem eigentlichen Aufgang sehen.

Beginnen wir mit dem horizontalen Koordinatensystem. Ausgangspunkt ist Bild 1. Die Kugel soll jetzt die Himmelssphäre darstellen, und die \(x-y-\)Ebene soll die Horizontebene eines irdischen Beobachters sein, der nicht auf einem der Pole steht (zu den Polen siehe Kasten unterhalb (4)). Dies sieht man in Bild 2 für Beobachter auf der nördlichen Hemisphäre. Der grüne Punkt in der Mitte der Kugel ist die Erde (nicht maßstäblich). Der Beobachter steht "oben" darauf; somit ist der schwarze Punkt, am höchsten Punkt der Kugel, der Zenit des Beobachters senkrecht über seinem Kopf. Die vier Himmelsrichtungen sind ebenfalls in Bild 2 eingetragen; ihre Orientierung ist so gewählt, dass die \(~x-\)Achse von Nord nach Süd verläuft, also negative \(~x-\)Werte im Norden, positive im Süden; die \(~y-\)Achse verläuft von West nach Ost mit negativen \(~y-\)Werten im Westen und positiven im Osten. Der Zenit hat die Koordinaten \((x,y,z)=(0,0,1)\). Der orangene Punkt stellt die Sonne dar (nicht maßstäblich; auch andere Himmelskörper könnten hier eingesetzt werden). Ihre Höhe \(~h~\) entspricht dem Winkel \(~\gamma~\) in Bild 1. Steht die Sonne unter dem Horizont, so ist \(~h \lt 0~\). – Für die Modellierung von geo-astronomischen Phänomenen, insbesondere für den Sonnenstand, ist eine andere Orientierung der Länge als in Bild 1 sinnvoll. Die Zählung soll nun im Norden bei \(~0°\) beginnen. Da die Sonne erst im Osten und später im Westen steht, läuft die Länge, anders als in Bild 1, im Uhrzeigersinn. Dies sieht man in Bild 2 (blauer Winkel, liegt in der Horizontebene, also der \(~x-y-\)Ebene); statt der Länge \(~\beta~\) aus Bild 1 wird hier die Himmelsrichtung \(~A~\) mit \(~90°\) für Osten, \(~180°\) für Süden und \(~270°\) für Westen genommen. – Für die Beschreibung des Astrolabiums bei Briefmarke # 69 wurde eine andere Orientierung gewählt.

Bild 2 Horizontale Koordinaten\(~(h,~A)~\). \(~h~\) ist die Höhe der Sonne, \(~A~\) die Himmelsrichtung der Sonne.

In der Transformation (1) wird somit \(~\gamma~\) zu \(~h~\) und \(~\beta~\) zu \(~180° - A~~\small{(\text{mod}~360°)}\normalsize~\):

Transformation horizontale Koordinaten → kartesische Koordinaten

\(h~\) Höhe der Sonne, \(~A~\) Himmelsrichtung der Sonne (Uhrzeigersinn)
\begin{array}{ll} \textbf{(2)} & x = -~cos~h~cos~A\\ ~ & y = cos~h~sin~A\\ ~ & z = sin~h \end{array}

Nun zum äquatorialen Koordinatensystem. Ausgangspunkt ist wieder Bild 1. Die Kugel soll auch hier die Himmelssphäre darstellen. Zur Unterscheidung vom horizontalen System lauten die kartesischen Koordinaten hier \((\tilde{x},~\tilde{y},~\tilde{z})~\); die \(\tilde{x}-\tilde{y}-\)Ebene enthält den Himmelsäquator – das ist die Projektion des irdischen Äquators auf die Himmelssphäre. Dies sieht man in Bild 3. Der schwarze Punkt mit den Koordinaten \((\tilde{x},~\tilde{y},~\tilde{z})=(0,0,1)\) ist der Nordpol der Himmelssphäre und liegt senkrecht über dem irdischen Nordpol. Der Beobachter steht auf einem Punkt, dessen geographische Länge mit der positiven Richtung der \(\tilde{x}-\)Achse zusammenfällt; seine geographische Breite sei \(~\textit{φ}~\) mit \(~|~\textit{φ}~| \lt 90°\) (zu \(~|~\textit{φ}~| = 90°\) siehe Kasten unterhalb (4)). Dann ist der blaue Punkt in Bild 3 die Projektion des Standorts des Beobachters auf die Himmelssphäre, also der Punkt am Himmel, der senkrecht über seinem Kopf steht. Der orangene Punkt stellt wieder die Sonne dar. Ihre Breite wird als Deklination \(~\delta~\) bezeichnet. Die Sonne läuft in einem Jahr in einer spiraligen Bahn vom südlichen Wendekreis (zu Winteranfang der Nordhalbkugel, Breite \(~\delta =-23,44°\)) zum nördlichen Wendekreis (zu Sommeranfang, Breite \(~\delta =23,44°\)) und zurück. Ist \(~\delta =0°\), so beschreibt die Sonne an einem Tag (näherungsweise) einen Großkreis um den Himmelsäquator, steht also senkrecht über dem irdischen Äquator. Ist \(~\delta \neq 0°\), so beschreibt die Sonne an einem Tag (näherungsweise) einen Kleinkreis auf der Himmelssphäre, parallel zur Äquatorebene, steht also senkrecht über dem irdischen Breitenkreis mit der Breite \(~\delta~\). Bei negativem \(~\delta~\) steht die Sonne senkrecht über der Südhalbkugel der Erde, bei positivem \(~\delta~\) über der Nordhalbkugel. Den Zusammenhang zwischen Deklination und Datum entnimmt man einer Tabelle. – Da ein Umlauf der Sonne auf einem dieser Groß- oder Kleinkreise einen Tag dauert, entspricht hier die Länge der Sonnenposition der Uhrzeit, die mit \(~\tau~\) bezeichnet und in Grad angegeben wird. Für die Modellierung des Schattenwurfs ist es sinnvoll, eine andere Orientierung der Länge als in Bild 1 zu wählen. Die Zählung soll – ähnlich wie im horizontalen System – um Mitternacht bei \(~0°\) beginnen und im Uhrzeigersinn laufen. Dies sieht man in Bild 3 (blauer Winkel, liegt in der Äquatorebene, also der \(\tilde{x}-\tilde{y}-\)Ebene); statt der Länge \(~\beta~\) aus Bild 1 wird hier die Uhrzeit \(~\tau~\) mit \(~90°\) für \(~06:00~\text{Uhr}~\), \(~180°\) für \(~12:00~\text{Uhr}~\) und \(~270°\) für \(~18:00~\text{Uhr}~\) genommen. – \(\tau~\) steht für die Ortszeit (wahre lokale Sonnenzeit), so wie sie von Sonnenuhren mit Zeitgleichungskorrektur angezeigt wird. Der Unterschied zur bürgerlichen Zeit, die durch unsere normalen Uhren angezeigt wird, ergibt sich aus der Zeitzone, dem Längengrad des Beobachters und der Zeitgleichung, siehe dazu Umrechnung Sonnenzeit / bürgerliche Zeit.

Bild 3 Äquatoriale Koordinaten\(~(\delta,~\tau)~\). \(~\delta~\) ist die Deklination der Sonne, \(~\tau~\) die Tageszeit in Grad.
\(\textit{φ}~\) ist der Breitengrad des Beobachters.

In der Transformation (1) wird somit \(~\gamma~\) zu \(~\delta~\) und \(~\beta~\) zu \(~180°-\tau~~\small{(\text{mod}~360°)}\normalsize~\):

Transformation äquatoriale Koordinaten → kartesische Koordinaten

\(\delta~\) Deklination, \(~\tau~\) Uhrzeit (Uhrzeigersinn)
\begin{array}{ll} \textbf{(3)} & \tilde{x} = -~cos~\delta~cos~\tau\\ ~ & \tilde{y} = cos~\delta~sin~\tau\\ ~ & \tilde{z} = sin~\delta \end{array}

Horizontales und äquatoriales System hängen eng zusammen. In Bild 3 steht der blaue Punkt senkrecht über dem Kopf des Beobachters, in Bild 2 der schwarze Punkt. Das bedeutet, dass das horizontale System durch eine Drehung aus dem äquatorialen System hervorgeht: Die \(x-z-\)Ebene ist gegenüber der \(\tilde{x}-\tilde{z}-\)Ebene um \(~90°-\textit{φ}~\) gedreht; Drehachse ist die \(\tilde{y}-\)Achse, die mit der \(y-\)Achse identisch ist. Die zugehörige Koordinatentransformation schaut man in einer Formelsammlung nach:

Transformation kartesische Koordinaten
äquatorial ↔ horizontal

φ Breitengrad des Beobachters
\begin{array}{ll} \textbf{(4)} & x~=~\tilde{x} \cdot \text{sin}~\textit{φ}~-~\tilde{z} \cdot \text{cos}~\textit{φ}~~~~~~~~~~~~\tilde{x}~=~x \cdot \text{sin}~\textit{φ}~+~z \cdot \text{cos}~\textit{φ}\\ ~ & y~=~\tilde{y}_{~~}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\tilde{y}~=~y\\ ~ & z~=~\tilde{x} \cdot \text{cos}~\textit{φ}~+~\tilde{z} \cdot \text{sin}~\textit{φ}~~~~~~~~~~~~\tilde{z}~=~-x \cdot \text{cos}~\textit{φ}~+~z \cdot \text{sin}~\textit{φ} \end{array}

Beobachter auf einem der Pole \(|~\textit{φ}~| = 90°\)

Aus (4) folgt: \(~|~\tilde{x}~| = x,~~|~\tilde{y}~| = y~\). Aber die Lage dieser Koordinaten, die den Sonnenstand beschreiben sollen, sind an den Polen nicht feststellbar. Deshalb sind dort \(~A~\) und \(~\tau~\) nicht definiert; siehe dazu (21b) und (46a).

Die Transformationen (2), (3) und (4) ermöglichen eine Vielzahl von Berechnungen für geo-astronomische Fragestellungen, wie z.B. Zeitpunkt und Himmelsrichtung des Sonnenaufgangs in Abhängigkeit von Datum und Breitengrad, Höhe und Himmelsrichtung der Sonne an einem bestimmten Ort zu einem bestimmten Zeitpunkt, Ermittlung der Uhrzeit aus dem Sonnenstand usw.

Die folgenden Formeln (5) - (20) folgen direkt aus (2), (3), (4) und setzen die fünf Größen \(~h~\), \(~A~\), \(~\delta~\), \(~\tau~\), \(~\textit{φ}~\) in Beziehung, mit \(~|~\textit{φ}~| \neq~90°\).

Natürliche Einschränkungen der Definitionsbereiche der Funktionen in den Formeln werden nicht immer explizit erwähnt; so gilt z.B. \(~cot(x)~\) nicht für \(~x = 0°~\) und \(~../cos(x)~\) nicht für \(~|~x~|=~90°~\).

Ab (21) werden dann die einzelnen Größen freigestellt, um u.a. Vorhersagen über den Stand der Sonne oder den Zeitpunkt von Ereignissen wie z.B. den Sonnenaufgang machen zu können.

Die genannten fünf Variablen können nicht beliebig in die Formeln ab (5) eingesetzt werden. Dies liegt daran, dass sie offenbar nicht unabhängig voneinander sind.

In der Regel werden drei Variablen zur Bestimmung einer vierten eingesetzt; deshalb sind (7) - (11) die wichtigsten Formeln. Das Tripel \(~(\textit{φ},~\delta,~\tau)~\) kann immer beliebig für die unabhängigen Variablen eingesetzt werden (siehe (8) und (10)), aber alle anderen Tripel von Eingabevariablen sind mit großer Vorsicht anzuwenden, da sie bei beliebiger Wahl evtl. in der Realität nicht vorkommen.

Diese Einschränkungen gelten natürlich nicht, wenn es sich bei den Eingaben um Werte aus tatsächlichen Himmelsbeobachtungen handelt.

Als Beispiel möge Formel (8) dienen. Die Größen \(~\textit{φ}~\), \(~\delta~\) und \(~\tau~\) können unabhängig voneinander gewählt werden, um \(~h~\) zu berechnen. Die Sonnenhöhe \(~h~\) lässt sich also – anschaulich gesprochen – aus dem Breitengrad des Beobachters \(~\textit{φ}~\), dem Datum (aus ihm lässt sich \(~\delta~\) ermitteln) und der Uhrzeit \(~\tau~\) berechnen, auch für nicht-beobachtete Eingabewerte, siehe (21). Aber die Berechnung von \(~\tau~\) mit (8) ist zwar über beobachtete Werte von \(~\textit{φ}~\),\(~\delta~\),\(~h~\) möglich (siehe (37)), jedoch nicht für beliebige Auswahlen dieser Eingabevariablen, da bei bekannten \(~\textit{φ}~\),\(~\delta~\) nicht alle \(~h~\)vorkommen können.

Insbesondere kann man in (5) und (6) nicht vier Größen beliebig einsetzen, um die fehlende zu berechnen.

Grundformeln

Spezialfälle für \(~\tau,~A\)

Wegen \(~y=\tilde{y}~\) folgt aus (2) und (3) für \(~h\neq \pm~90°~\):
\begin{array}{ll} \textbf{(12)} & \tau \in (~0°,~180°)~~~~\Leftrightarrow~~~~A \in (~0°,~180°)\\ ~ & \small{\text{Vor dem Mittag steht die Sonne in oestlicher Richtung.}}\normalsize\\ ~ & ~\\ ~ & \tau \in (~180°,~360°)~~~~\Leftrightarrow~~~~A \in (~180°,~360°)\\ ~ & \small{\text{Nach dem Mittag steht die Sonne in westlicher Richtung.}}\normalsize\\ ~ & ~\\ ~ & \small{\text{Um 00:00 Uhr und um 12:00 Uhr steht die Sonne entweder im Sueden oder im Norden:}}\normalsize\\ ~ & \tau = 0°~~\wedge~~A = 0°~~~~\Leftrightarrow~~~~\textit{φ} \gt -~\delta~~~~~~~~~~~~~\small{(\text{cos}~h~=~\text{sin}~(\delta + \textit{φ}) \gt 0~)}\normalsize\\ ~ & \tau = 0°~~\wedge~~A = 180°~~~~\Leftrightarrow~~~~\textit{φ} \lt -~\delta~~~~~~~~~~~~~\small{(\text{– cos}~h~=~\text{sin}~(\delta + \textit{φ}) \lt 0~)}\normalsize\\ ~ & \tau = 180°~~\wedge~~A = 0°~~~~\Leftrightarrow~~~~\textit{φ} \lt ~\delta~~~~~~~~~~~~~\small{(\text{cos}~h~=~\text{sin}~(\delta - \textit{φ}) \gt 0~)}\normalsize\\ ~ & \tau = 180°~~\wedge~~A = 180°~~~~\Leftrightarrow~~~~\textit{φ} \gt ~\delta~~~~~~~~~~~~~\small{(\text{– cos}~h~=~\text{sin}~(\delta - \textit{φ}) \lt 0~)}\normalsize \end{array} Begründungen in Klammern jeweils mit (5) ↑

(12) ist nicht anwendbar für \(h=\pm~90°\), denn in diesem Fall steht die Sonne im Zenit oder Nadir, also gibt es keine Himmelsrichtung \(~A~\).

Aus den Additionstheoremen für Sinus und Cosinus folgt (bei \(~\pm ~\) oder \(~\mp ~\) in (13) - (20) gilt das obere Zeichen für \(~A =0°~\)(Norden), das untere für \(~A =180°~\)(Süden)) :

\(\large{\odot} \normalsize~~~~~~\)Für \(~\tau=0°~~~\)Mitternacht: \begin{array}{ll} \textbf{(13)} & \text{cos}~h~=~\pm~~\text{sin}~(\delta + \textit{φ})~~~~~~~~~~~\small{(\text{mit (5)})}\normalsize\\ \textbf{(14)} & \text{sin}~h~=~- \text{cos}~(\delta + \textit{φ})~~~~~~~~~~\small{(\text{mit (8)})}\normalsize\\ \textbf{(15)} & \text{cos}~\delta~=~- \text{sin}~(h \mp \textit{φ})~~~~~~~~~~~\small{(\text{mit (6)})}\normalsize\\ \textbf{(16)} & \text{sin}~\delta~=~\pm \text{cos}~(h \mp \textit{φ})~~~~~~~~~~~\small{(\text{mit (9)})}\normalsize \end{array} \(\large{\odot} \normalsize~~~~~~\)Für \(~\tau=180°~~~\)Mittag: \begin{array}{ll} \textbf{(17)} & \text{cos}~h~=~\pm~~\text{sin}~(\delta - \textit{φ})~~~~~~~~~~~\small{(\text{mit (5)})}\normalsize\\ \textbf{(18)} & \text{sin}~h~=~\text{cos}~(\delta - \textit{φ})~~~~~~~~~~\small{(\text{mit (8)})}\normalsize\\ \textbf{(19)} & \text{cos}~\delta~=~\text{sin}~(h \mp \textit{φ})~~~~~~~~~~~\small{(\text{mit (6)})}\normalsize\\ \textbf{(20)} & \text{sin}~\delta~=~\pm \text{cos}~(h \mp \textit{φ})~~~~~~~~~~~\small{(\text{mit (9)})}\normalsize \end{array}

Höhe der Sonne über oder unter dem Horizont

\(h~\) Sonnenhöhe, \(~A~\) Himmelsrichtung der Sonne, \(~\delta~\) Deklination, \(~\tau~\) Uhrzeit, \(~\textit{φ}~\) Breitengrad des Beobachters \begin{array}{ll} \textbf{(21)} & h~=~\text{arcsin}~(-\text{cos}~\delta~~\text{cos}~\tau~~\text{cos}~\textit{φ}~+~\text{sin}~\delta~~\text{sin}~\textit{φ})~~~~~~~~~\small{(\text{mit (8)})}\normalsize\\ ~ & ~\\ \textbf{(21a)} & \text{Fuer}~~|\textit{φ}| \neq 90°~~\text{gilt: Wegen}~~h = \text{arcsin}~(a~\text{cos}~\tau + b)~~~~\text{mit}~~a \lt 0~~\text{waechst}~~h~~\text{streng monoton fuer}~~\tau \in (0°,~180°)\\ ~ & \text{und faellt streng monoton fuer}~~\tau \in (180°,~360°).\\ ~ & \text{Fuer}~~h_{max}~~\text{und}~~h_{min}~~\text{siehe (25)}.\\ ~ & ~\\ \textbf{(21b)} & \text{Hoehe der Sonne an den Polen:}~~~h =\pm~\delta~~~~~~\small{\text{für}}\normalsize~~~\textit{φ}=\pm~90° \end{array} (21) ist die Hauptformel zur Bestimmung von \(~h~\), da in der Regel \(~\textit{φ}~\), \(~\delta~\) und \(~\tau~\) als Eingabewerte zur Verfügung stehen. Die folgenden Formeln verwenden auch \(~A~\) als Eingabewert. \begin{array}{ll} \textbf{(22)} & h~=~\pm~\text{arccos}~(\text{cos}~\delta~~\text{sin}~\tau~/~\text{sin}~A)~~~~~~\small{\text{fuer}~~\tau,~A~\neq~0°,~180°}~~~~~~~~~\small{(\text{mit (7))}}\normalsize \end{array} In (22) steht das positive Vorzeichen für die Zeit zwischen Sonnenaufgang und -untergang und für den Polarsommer (d.h. wenn die Sonne den ganzen Tag über dem Horizont bleibt, siehe (50) und (63));
das negative Vorzeichen steht für die Zeit zwischen Sonnenuntergang und -aufgang und für den Polarwinter (d.h. wenn die Sonne den ganzen Tag unter dem Horizont bleibt, siehe (50) und (63)).
Die Zeiten für Sonnenaufgang und -untergang stehen in (41) und (42).

Für \(~\tau,~A~=~0°,~180°~\), also für mittags und mitternachts, reichen die Eingaben von \(~\delta,~\tau,~A~\) zur Bestimmung von \(~h~\) nicht aus, da \(~\tau~\) und \(~A~\) nicht unabhängig voneinander sind.
Also geht es nicht ohne \(~\textit{φ}~\), siehe (25) und (26).

\begin{array}{ll} \textbf{(23)} & h~=~\text{arctan}~(\text{cos}~A~~\text{tan}~\textit{φ}~-~\text{cot}~\tau~~\text{sin}~A~/~\text{cos}~\textit{φ})~~~~~~~~~\small{(\text{mit (11)})}\normalsize\\ ~ & ~ \\ \textbf{(24)} & \text{Die Bestimmung von}~~h~~\text{mittels}~~\textit{φ},~~\delta~~\text{und}~~A~~\text{ist umstaendlicher, aber mit (9) moeglich.}\\ ~ & \text{Man erhaelt eine Gleichung der Form}~~a~\text{cos}~h + b~\text{sin}~h = c~~,~\text{die mit cos}~h = \sqrt{1-\text{sin}^2~h}~~\text{loesbar ist.} \end{array}

Mitternachts- und Mittagshöhe der Sonne
\begin{array}{lll} \textbf{(25)} & \tau = 0° & ~\rightarrow~~~h~=~|~\textit{φ}+\delta~|-90°\\ ~ & ~ & ~~~~~~\small{\text{Jahresmaximum}~=~|~\textit{φ}~|- 66,56°}\normalsize\\ ~ & ~ & ~~~~~~\small{\text{Jahresminimum = max}~\{-90°,-113,44° + |~\textit{φ}~|~\}}\normalsize\\ ~ & ~ & ~\\ ~ & \tau =180° & ~\rightarrow~~~h~=~90°-|~\textit{φ}-\delta~|\\ ~ & ~ & ~~~~~~\small{\text{Jahresmaximum = min}~\{~90°,~113,44° - |~\textit{φ}~|~\}}\normalsize\\ ~ & ~ & ~~~~~~\small{\text{Jahresminimum}~=~66,56° - |~\textit{φ}~|}\normalsize \end{array} Dies folgt mit (14) aus \(~~\text{sin}~h~=-~\text{cos}~|~\textit{φ} + \delta~|~=-~\text{sin}~(~90° \pm |~\textit{φ} + \delta~|~)~=~\text{sin}~(\mp |~\textit{φ} + \delta~|~-90°)~\) und mit (18) aus \(~~\text{sin}~h~=~\text{cos}~|~\textit{φ} - \delta~|~=~\text{sin}~(~90° \pm |~\textit{φ} - \delta~|~)~\).

Die Jahresmaxima und -minima gelten auch für die Pole, unabhängig von der Uhrzeit.

Höhe der Sonne im Norden und im Süden

Im Folgenden steht "+" für \(~\tau = 180°\) und "—" für \(~\tau = 0°\).
\begin{array}{lll} \textbf{(26)} & A = 0°~~~\wedge~~~\delta \gt \pm~\textit{φ} & ~\rightarrow~~~h~=~\textit{φ}~\pm~(90° - \delta)~~~~~~\small{\text{Für}~~\textit{φ} \in (-~\delta,~\delta)~~\text{gelten beide Vorzeichen (Sonne zweimal täglich im Norden).}}\\ ~ & ~ & ~\\ ~ & A = 180°~~~\wedge~~~\delta \lt \pm~\textit{φ} & ~\rightarrow~~~h~=~-~\textit{φ}~\pm~(90° + \delta)~~~~~~\small{\text{Für}~~\textit{φ} \in (\delta, -~\delta)~~\text{gelten beide Vorzeichen (Sonne zweimal täglich im Süden).}} \end{array} Dies folgt aus (25) und (12). Für \(~\delta = \pm~\textit{φ}~\) würde sich \(~|~h~| = 90°\) ergeben, aber dafür ist \(~A~\) nicht definiert; siehe auch (27) und (29).

Bild 4 Beispiele zu (21), (21a), (25) Links:\(~~~\textit{φ} = 50°,~~\delta = 9°~~~~~~\)Mitte:\(~~~\textit{φ} = 75°,~~\delta = 22°~~~~~~\)Rechts:\(~~~\textit{φ} = -86°,~~\delta = 19°\)

h im Jahreslauf

Bild 5    Beispiele zu (25)
                Mittagshöhe der Sonne im Jahresverlauf zwischen Winter- und Sommeranfang
                Links:\(~~~\textit{φ} = 12°~~~~~~\)Rechts:\(~~~\textit{φ} = -42°\)

Jahresmax und -min

Bild 6 Zu (25) Jahresmaximum und -minimum der Mittagshöhe der Sonne in Abhängigkeit vom Breitengrad

Beispiel 1 — zu (24)

Durchläuft die Sonne innerhalb eines Tages alle Himmelsrichtungen, so hat die Gleichung in (24) genau eine Lösung für \(~h~\), siehe Felder 1 und 4 in Bild 7. Eine oder keine Lösung erhält man in den Fällen, die in den Feldern 5 bis 9 dargestellt sind. Keine, eine oder zwei Lösungen erhält man in den Fällen, die in den Feldern 2 und 3 dargestellt sind. Bild 7 gibt also genauen Aufschluss darüber, wieviele Lösungen es zu einem konkreten \(~A~\) gibt.

Bei Fragestellungen wie in diesem Beispiel wird die Deklination \(~\delta~\) während eines Tages als konstant angenommen, was natürlich nur näherungsweise gilt (siehe folgendes Beispiel).
\begin{array}{lllll} \textit{φ} = 50° & \delta = 10° & A = 85° & \rightarrow~~~h \approx 8,9° & \small{\text{Feld 1 – }~~\textcolor{orange}{\text{Zur Genauigkeit: Diese Deklination schwankt im Tagesverlauf um ca. 0,175°.}}}\normalsize\\ ~ & ~ & ~ & ~ & \small{\textcolor{orange}{\text{Das ergibt ca.}~~8,7° \lt h \lt 9,1°.}}\normalsize\\ ~ & ~ & ~ & ~ & ~\\ \textit{φ} = -16° & \delta = 21° & A = 300° & \rightarrow~~~h_1 \approx 19,9°~~~h_2 \approx -79,5° & \small{\text{Feld 3 – Sonne läuft in der zweiten Tageshälfte vom Norden westwärts und zurück.}}\normalsize\\ ~ & ~ & ~ & ~ & ~\\ \textit{φ} = 16° & \delta = 16° & A = 95° & \rightarrow~~~\text{keine Lösung} & \small{\text{Feld 5 – Sonne erreicht keine südlichen Richtungen zwischen Ost und West;}}\normalsize\\ ~ & ~ & ~ & ~ & \small{\text{mittags läuft sie über den Zenit von Ost nach West.}}\normalsize\\ ~ & ~ & ~ & ~ & ~\\ \textit{φ} = 20° & \delta = -20° & A = 180° & \rightarrow~~~h = 50° & \small{\text{Feld 8 – Lösung ergibt sich auch aus (25).}}\normalsize \end{array}

Himmelsrichtung der Sonne

\(h~\) Sonnenhöhe, \(~A~\) Himmelsrichtung der Sonne, \(~\delta~\) Deklination, \(~\tau~\) Uhrzeit, \(~\textit{φ}~\) Breitengrad des Beobachters
\begin{array}{lll} \textbf{(27)} & \tau = 0°~\small{\text{(Mitternacht)}} & \rightarrow ~~A~=~0°~\small{\text{(Norden)}}\normalsize~~\text{für}~~~\textit{φ} \gt -~\delta~~~~\text{und}~~~~A~=~180°~\small{\text{(Süden)}}\normalsize~~\text{für}~~~\textit{φ} \lt -~\delta\\ ~ & ~ & ~~~~~~~~~~~~~~~\small{\textit{φ} =-\delta~~~~\leftrightarrow~~~~h = -90°~~~~\leftrightarrow~~~~\text{Sonne im Nadir (keine Himmelsrichtung}~~A)} \normalsize\\ ~ & ~ & ~\\ ~ & \tau \in (0°,~180°) & \rightarrow ~~A~=~\text{arccot}~(\text{cot}~\tau~~\text{sin}~\textit{φ}~+~\text{tan}~\delta~~\text{cos}~\textit{φ}~/~\text{sin}~\tau)~~~~\small{\text{(beachte Kasten unter (4))}}\normalsize\\ ~ & ~ & ~\\ ~ & \tau = 180°~\small{\text{(Mittag)}} & \rightarrow ~~A~=~0°~\small{\text{(Norden)}}\normalsize~~\text{für}~~~\textit{φ} \lt \delta~~~~\text{und}~~~~A~=~180°~\small{\text{(Süden)}}\normalsize~~\text{für}~~~\textit{φ} \gt \delta\\ ~ & ~ & ~~~~~~~~~~~~~~~\small{\textit{φ} = \delta~~~~\leftrightarrow~~~~h = 90°~~~~\leftrightarrow~~~~\text{Sonne im Zenit (keine Himmelsrichtung}~~A)} \normalsize\\ ~ & ~ & ~\\ ~ & \tau \in (180°,~360°) & \rightarrow ~~A~=~\text{arccot}~(\text{cot}~\tau~~\text{sin}~\textit{φ}~+~\text{tan}~\delta~~\text{cos}~\textit{φ}~/~\text{sin}~\tau)~+~180°~~~~\small{\text{(beachte Kasten unter (4))}}\normalsize \end{array} (27) folgt aus (10), (12), (14), (18). — Hinweis: Bei der Berechnung von \(~A~\) mit Mathematica muss berücksichtigt werden, dass dort der arccot die Umkehrfunktion von \(~\text{cot}:[-\pi/2,~\pi/2]\setminus\{0\}~\rightarrow~\textbf{R}~\) ist, entgegen der üblicheren Umkehrfunktion von \(~\text{cot}:(0,~\pi)~\rightarrow~\textbf{R}~\), die auch hier verwendet wird. Dies lässt sich heilen, indem man die Mathematica-Funktion acot[x_]:= ArcCot[x] + If[x<0,π,0] definiert.

Es folgt: \begin{array}{ll} \textbf{(28)} & A(\tau) = 360° - A(360° - \tau)~~~\text{für}~~~\tau \neq 0°,~180° \end{array}
Monotonie von \(~A(\tau)~\) mittels (27) durch Ableiten (\(~0°~\) und \(~360°~\) werden miteinander identifiziert); beachte Kasten unterhalb (4): \begin{array}{lll} \textbf{(29)} & \textit{φ} \gt |~\delta~| & \rightarrow ~~A(\tau)~~\text{wächst streng monoton.}\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(0°)=0°~~\rightarrow~~\text{Osten}~~\rightarrow~~A(180°)=180°~~\rightarrow~~\text{Westen}~~\rightarrow~~A(360°)=360°} \normalsize\\ ~ & ~ & ~\\ ~ & \textit{φ} \in (~\delta~,- \delta~) & \rightarrow ~~A(\tau)~~\text{wächst streng monoton für}~~\tau \in (\tau_0~,~360°-\tau_0)~,~\text{fällt sonst}~~\small({\text{beachte}~~\delta \lt 0°).} \normalsize\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(0°)=180°~~\rightarrow~~A(\tau_0)~\text{östlich}~~\rightarrow~~A(180°)=180°~~\rightarrow~~A(360°-\tau_0)~\text{westlich}~~\rightarrow~~A(360°)=180°} \normalsize\\ ~ & ~ & ~\\ ~ & \textit{φ} \in (- \delta~,~\delta~) & \rightarrow ~~A(\tau)~~\text{fällt streng monoton für}~~\tau \in (\tau_0~,~360°-\tau_0)~,~\text{wächst sonst}~~\small({\text{beachte}~~\delta \gt 0°).} \normalsize\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(0°)=0°~~\rightarrow~~A(\tau_0)~\text{östlich}~~\rightarrow~~A(180°)=0°~~\rightarrow~~A(360°-\tau_0)~\text{westlich}~~\rightarrow~~A(360°)=360°} \normalsize\\ ~ & ~ & ~\\ ~ & \textit{φ} \lt -~|~\delta~| & \rightarrow ~~A(\tau)~~\text{fällt streng monoton}.\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(0°)=180°~~\rightarrow~~\text{Osten}~~\rightarrow~~A(180°)=0°~~\rightarrow~~\text{Westen}~~\rightarrow~~A(360°)=180°} \normalsize \end{array}
\[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\tau_0~=~\text{arccos}~(-\text{tan}~\textit{φ}~/~\text{tan}~\delta~)\] \[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~A(\tau_0)~=~\text{arccot}~ \left(\frac{-\text{sin}~\textit{φ}~~\text{tan}~\textit{φ}~/~\text{tan}~\delta~+~\text{tan}~\delta~~\text{cos}~\textit{φ}}{\sqrt{1-\text{tan}^2~\textit{φ}~/~\text{tan}^2~\delta}}\right)\] \[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~A(360° - \tau_0)~=~360° - A(\tau_0)\]
\begin{array}{lll} ~ & ~~~~~~~~\textit{φ} = \delta \gt 0° & \rightarrow~~A(\tau)~~\text{ist in}~~\tau = 180°~\text{nicht definiert und wächst streng monoton.}\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(0°)=0°~~\rightarrow~~\text{östlich zum Zenit mit Mittags-Grenzwert Osten}~~\rightarrow~~\text{westlich vom Zenit mit Mittags-Grenzwert Westen}~~\rightarrow~~A(360°)=360°} \normalsize\\ ~ & ~~~~~~~~\textit{φ} = \delta \lt 0° & \rightarrow~~A(\tau)~~\text{ist in}~~\tau = 180°~\text{nicht definiert und fällt auf beiden Definitionsintervallen streng monoton.}\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(0°)=180°~~\rightarrow~~\text{östlich zum Zenit mit Mittags-Grenzwert Osten}~~\rightarrow~~\text{westlich vom Zenit mit Mittags-Grenzwert Westen}~~\rightarrow~~A(360°)=180°} \normalsize\\ ~ & ~~~~~~~~\textit{φ} = \delta = 0° & \rightarrow~~A(\tau)~~\text{ist in}~~\tau = 180°~\text{nicht definiert und ist auf beiden Definitionsintervallen konstant.}\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{A(\tau)=90°~~\text{für}~~\tau \lt 180°,~~~A(\tau)=270°~~\text{für}~~\tau \gt 180°~,~~\text{siehe (44)}}\normalsize\\ ~ & ~~~~~~~~\textit{φ} = -\delta \gt 0° & \rightarrow~~A(\tau)~~\text{ist in}~~\tau = 0°~\text{nicht definiert und wächst streng monoton.}\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{\text{Sonne im Nadir für}~~\tau = 0°,~~\text{Nach-Mitternachts-Grenzwert von}~~A(\tau)~~\text{für}~~\tau \rightarrow 0°~~\text{ist}~~90°~,~~A(180°) = 180°,~\text{Vor-Mitternachts-Grenzwert von}~~A(\tau)~~\text{für}~~\tau \rightarrow 360°~~\text{ist}~~270°}\normalsize\\ ~ & ~~~~~~~~\textit{φ} = -\delta \lt 0° & \rightarrow~~A(\tau)~~\text{ist in}~~\tau = 0°~\text{nicht definiert und fällt streng monoton.}\\ ~ & ~ & ~~~~~~~~~~~~~~~~~\small{\text{Sonne im Nadir für}~~\tau = 0°,~~\text{Nach-Mitternachts-Grenzwert von}~~A(\tau)~~\text{für}~~\tau \rightarrow 0°~~\text{ist}~~90°~,~~A(180°) = 0°,~\text{Vor-Mitternachts-Grenzwert von}~~A(\tau)~~\text{für}~~\tau \rightarrow 360°~~\text{ist}~~270°}\normalsize \end{array}
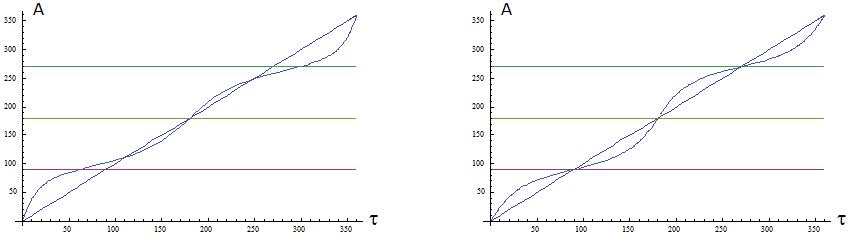
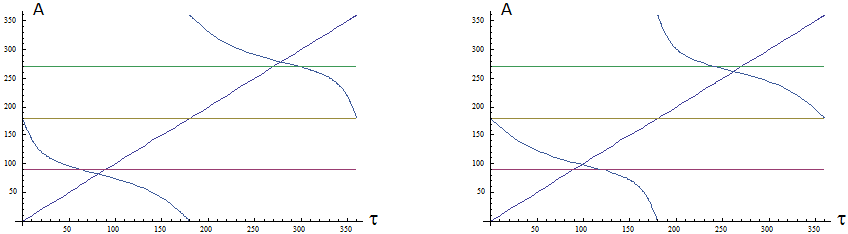
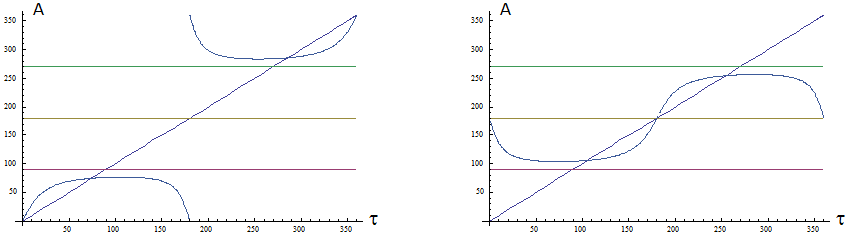
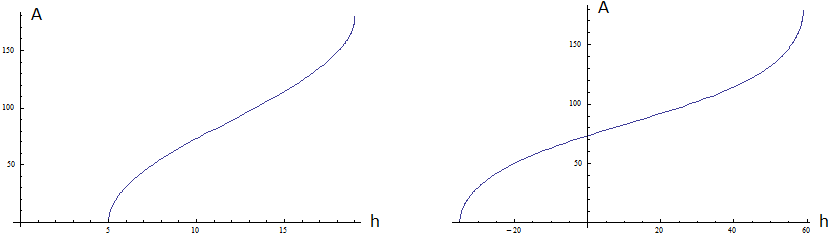
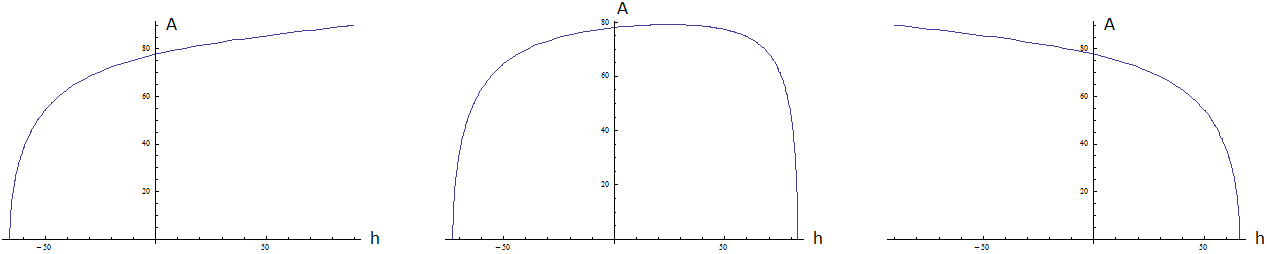
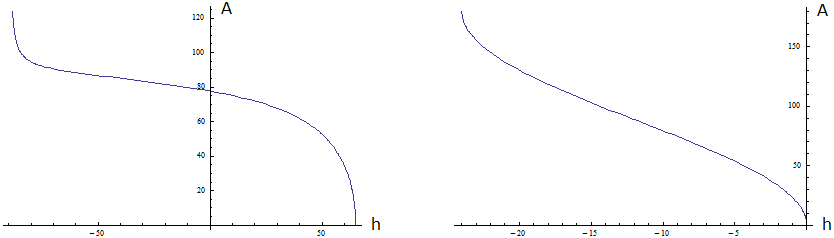
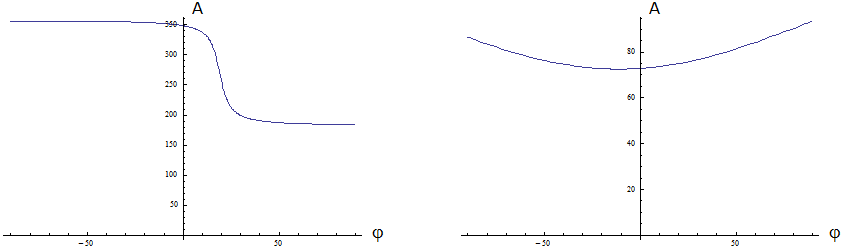
Aus (12) und (29) folgt: \begin{array}{ll} \textbf{(30)} & \text{Wertebereich von} ~A(\tau)~,~\text{östlichster und westlichster Punkt der Sonnenbahn :} \end{array} Alle wesentlichen Informationen stehen in Bild 7. Die Reihenfolge der neun Felder folgt (29). Beachte Kasten unterhalb (4).

Jedes Feld ist von \(~00:00~\text{Uhr}~\) über \(~12:00~\text{Uhr}~\) bis \(~24:00~\text{Uhr}~(= 00:00~ \text{Uhr})~\) zu lesen. Die orangenen Linien stehen für die Himmelsrichtungen, die von der Sonne durchlaufen werden. Hierbei wird für stationäre Beobachter eine kleine Ungenauigkeit in Kauf genommen, da sich \(~\delta~\) im Laufe eines Tages leicht ändert.

Die orangenen Bereiche korrespondieren mit den Definitionsbereichen von \(~A(\tau)~\), die jeweils links unten in Blau eingetragen sind.

\(\tau_1 = 360° - \tau_0~,~~A_0 = A(\tau_0),~~A_1 = A(\tau_1)\)

\(\large{\odot} \normalsize~~~~\)Östlichster Punkt der Sonnenbahn:
\(~~~~~~~~~~~~90°~\text{Osten}~\) in den Feldern 1, 4, 7
\(~~~~~~~~~~~~A_0~\) in den Feldern 2, 3
\(~~~~~~~~~~~~\text{Grenzwert Osten}~\) in den Feldern 5, 6, 8, 9

\(\large{\odot} \normalsize~~~~\)Westlichster Punkt der Sonnenbahn:
\(~~~~~~~~~~~~270°~\text{Westen}~\) in den Feldern 1, 4, 7
\(~~~~~~~~~~~~A_1~\) in den Feldern 2, 3
\(~~~~~~~~~~~~\text{Grenzwert Westen}~\) in den Feldern 5, 6, 8, 9

Wertebereiche

Bild 7 Himmelsrichtungen der Sonne innerhalb eines Tages in Abhängigkeit von \(~\delta~\) und \(~\textit{φ}~\)

Aus (29) und (30) folgt: \begin{array}{ll} \textbf{(31)} & \text{Sonne steht mittags} \textbf{ und } \text{mitternachts im Süden}~~~~\Leftrightarrow~~~~\textit{φ} \in (\delta,~-~\delta)~~~~~~~\small{(\rightarrow ~~~\delta~\lt~0)}\normalsize\\ ~~~~~~~~ & \text{Sonne steht mittags} \textbf{ und } \text{mitternachts im Norden}~~~~\Leftrightarrow~~~~\textit{φ} \in (-~\delta,~\delta)~~~~~~~\small{(\rightarrow ~~~\delta~\gt~0)}\normalsize\\ ~~~~~~~~ & ~~~~~~\text{Nur in diesen beiden Fällen und für}~~\textit{φ} = \pm~\delta~~\text{kommen nicht alle Himmelsrichtungen}~~A~~\text{im Laufe eines Tages vor.} \end{array}
Bis hierhin wurde in (27) - (31) \(~A~\) in Abhängigkeit von \(~\delta,~\textit{φ},~\tau~\) untersucht. Nun folgen andere Tripel der unabhängigen Variablen. \begin{array}{ll} \textbf{(32)} & A~=~\text{arccos}~((\text{sin}~\delta - \text{sin}~h~~\text{sin}~\textit{φ})~/~(\text{cos}~h~~\text{cos}~\textit{φ}))~~~~~\vee\\ ~ & A~=~360°-\text{arccos}~((\text{sin}~\delta - \text{sin}~h~~\text{sin}~\textit{φ})~/~(\text{cos}~h~~\text{cos}~\textit{φ})) \end{array} (32) folgt aus (9). Die Lösung ist zweideutig, da das gleiche \(~h~\) vor und nach dem Mittag zu beobachten ist.
Welche \(~h~\) in Frage kommen, folgt aus (25).
(32) ist nicht anwendbar für \(h=\pm~90°\). In diesem Fall steht die Sonne im Zenit oder Nadir, also gibt es keine Himmelsrichtung \(~A~\), siehe (36).

\begin{array}{lll} \textbf{(33)} & \tau~\in (0°,~180°)~~\rightarrow~~~ & A~=~\text{arcsin}~(\text{cos}~\delta~~\text{sin}~\tau~/~\text{cos}~h)~~~~~~~\vee\\ ~ & ~ & A~=~180°-\text{arcsin}~(\text{cos}~\delta~~\text{sin}~\tau~/~\text{cos}~h)\\ ~ & \tau~\in (180°,~360°)~~\rightarrow~~~ & A~=~\text{arcsin}~(\text{cos}~\delta~~\text{sin}~\tau~/~\text{cos}~h)+ 360°~~~~~\vee\\ ~ & ~ & A~=~180°-\text{arcsin}~(\text{cos}~\delta~~\text{sin}~\tau~/~\text{cos}~h) \end{array} (33) folgt aus (7) und ist wie (32) nicht anwendbar für \(h=\pm~90°\).

\(\text{sin}~A~=~\text{cos}~\delta~~\text{sin}~\tau~/~\text{cos}~h~\) hat keine Lösung für \(~A~\), wenn die rechte Seite nicht in \([-1,~1~]~\) ist.

\(\text{sin}~A~=~\text{cos}~\delta~~\text{sin}~\tau~/~\text{cos}~h~\in~[-1,~1~]~\) hat keine oder zwei Lösungen für \(~A~\), wenn \(~\delta,~\tau,~h~\) willkürlich vorgegeben werden, und zwei Lösungen, wenn diese Eingaben aus Beobachtungen stammen; die beiden Lösungen fallen für \(~A = 90°\) in eine zusammen. In dieser Weise ist "\(\vee\)" zu verstehen. Dies harmoniert mit den Lösungen der Gleichung (8) / (51) für \(~\textit{φ}~\).

\begin{array}{ll}\textbf{(34)} & \text{Die Bestimmung von}~~A~~\text{mittels}~~\textit{φ},~~\tau~~\text{und}~~h~~\text{ist umständlicher, aber mit (11) möglich.}\\ ~ & \text{Man erhält eine Gleichung der Form}~~a~\text{cos}~A + b~\text{sin}~A = c~~,~\text{die mit sin}~A = \sqrt{1-\text{cos}^2~A}~~~\text{für}~~\tau \lt 180°~~\text{und mit sin}~A = -\sqrt{1-\text{cos}^2~A}~~~\text{für}~~\tau \gt 180°~~\text{lösbar ist.} \end{array}

Wo steht die Sonne bei ihrem Aufgang / Untergang ?\(~~~~~~h=0°\) \begin{array}{ll} \textbf{(35)} & \small{\text{Aufgang:}}\normalsize~~~~~A~=~\text{arccos}~(\text{sin}~\delta~/~\text{cos}~\textit{φ})\\ ~ & \small{\text{Untergang:}}\normalsize~~~~~A~=~360°-\text{arccos}~(\text{sin}~\delta~/~\text{cos}~\textit{φ}) \end{array} Am Äquator: \(A_{auf} = 90° - \delta~,~~~A_{unter} = 270° + \delta\)

(35) folgt aus (32).
(35) ist nicht anwendbar im Polarsommer und -winter (d.h. wenn die Sonne den ganzen Tag über bzw. den ganzen Tag unter dem Horizont bleibt, denn dann ist \(~h \neq 0°\); siehe (50) und (63)).

Sonne im Zenit / Nadir\(~~~~~~h=\pm~90°\)

Dies sind die Fälle, in denen es keine Himmelsrichtung gibt, so dass (32) - (34) nicht angewendet werden können. Aus (25) und (26) folgt:
\begin{array}{lll} \textbf{(36)} & \tau = 0°~\small{\text{(Mitternacht)}}\normalsize~~~\wedge~~~\textit{φ}=-~\delta~ & \rightarrow~~~~\text{Sonne im Nadir}\\ ~ & \tau = 180°~\small{\text{(Mittag)}}\normalsize~~~\wedge~~~\textit{φ}=\delta~ & \rightarrow~~~~\text{Sonne im Zenit} \end{array}

\(~~~~~~~~\text{a)}~~~\textit{φ} = 26°~~~~\delta = -13°~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{b)}~~~\textit{φ} = 24°~~~~\delta = 0°\)

A im Tagesverlauf

\(~~~~~~~~\text{c)}~~~\textit{φ} = -26°~~~~\delta = 13°~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{d)}~~~\textit{φ} = -26°~~~~\delta = -13°\)

A im Tagesverlauf

\(~~~~~~~~\text{e)}~~~\textit{φ} = 4°~~~~\delta = 14°~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{f)}~~~\textit{φ} = 4°~~~~\delta = -14°\)

Bild 8 Beispiele zu (27), (29), (31) siehe auch Beispiel 6
Zur besseren Orientierung wurden auch die Winkelhalbierende sowie \(~A = 90°, 180°, 270°\) eingezeichnet.

Die Kurvenverläufe in Bild 8 zeigen: Um \(~06:00~\text{Uhr }~(\tau = 90°)~\) ist im Nordsommer \(~(\delta \gt 0°)~~A \lt 90°\) und im Nordwinter \(~(\delta \lt 0°)~~A \gt 90°\). Um \(~18:00~\text{Uhr }~(\tau = 270°)~\) ist es umgekehrt. Dies folgt auch direkt aus (27).

A in Abhängigkeit von h

\(~~~~~~~~\text{a)}~~~\textit{φ} = 83°~~~~\delta = 12°~~~~h \in [~5°, 19°]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{b)}~~~\textit{φ} = 43°~~~~\delta = 12°~~~~h \in [-35°, 59°]\)

A in Abhängigkeit von h

\(~~~~~~~~\text{c)}~~~\textit{φ} = 12°~~~~\delta = 12°~~~~h \in [-66°, 90°]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{d)}~~~\textit{φ} = 5°~~~~\delta = 12°~~~~h \in [-73°, 83°]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{e)}~~~\textit{φ} = -12°~~~~\delta = 12°~~~~h \in [-90°, 66°]\)

A in Abhängigkeit von h

\(~~~~~~~~\text{f)}~~~\textit{φ} = -13°~~~~\delta = 12°~~~~h \in [-89°, 65°]~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{g)}~~~\textit{φ} = -78°~~~~\delta = 12°~~~~h \in [-24°, 0°]\)

Bild 9 Beispiele zu (32)

Die Definitionsbereiche für \(~h~\) ergeben sich aus (25). Bild 9 zeigt nur die erste Tageshälfte; aus (32) ergibt sich die Symmetrie für die zweite Tageshälfte. – Bild 9 zeigt auch Beispiele für (35) mit \(~h = 0°~\) für den Sonnenaufgang und in c) und e) für (36).

Beispiel 2 — zu (33)
\begin{array}{llll} \delta = 12° & \tau = 170° & h = 66° & \rightarrow~~~A_1 \approx 24,7°~~~A_2 \approx 155,3° \end{array} Dies harmoniert mit (8) / (51): Bestimmt man mit diesen \(~\delta,~\tau,~h~\) zwei Werte für \(~\textit{φ}~\), so erhält man \(~\textit{φ}_1 \approx -9,8°\) und \(~\textit{φ}_2 \approx 34,2°\), die sich mit (5), (6) überprüfen lassen; setzt man diese Werte in (27) ein, erhält man die gleichen Lösungen \(~A_1,~A_2~\).

Beispiel 3 — zu (34)
\begin{array}{lllll} \textit{φ} = 56° & \tau = 265° & h = 18,9° & \rightarrow~~~A \approx 277,3° & ~~~~~\delta \approx 19,6°\\ \textit{φ} = 4° & \tau = 15° & h = -68,6° & \rightarrow~~~A_1 \approx 44,1°~~~A_2 \approx 138,1° & ~~~~~\delta_1 \approx 11,3°~~~\delta_2 \approx -19,6° \end{array} Die Werte für \(~\delta~\) wurden zusätzlich aufgenommen und mit (8) / (48) berechnet; zur Überprüfung werden sie in (5) und (6) eingesetzt. Außerdem kann man \(~\textit{φ},~\delta,~\tau~\) in (21) und (27) einsetzen und damit \(~h~\) und \(~A~\) reproduzieren.

Bestimmung der Uhrzeit aus dem Sonnenstand

\(\tau~\) Uhrzeit, \(~\textit{φ}~\) Breitengrad des Beobachters, \(~\delta~\) Deklination, \(h~\) Sonnenhöhe, \(~A~\) Himmelsrichtung der Sonne
\begin{array}{ll} \textbf{(37)} & \tau~=~\text{arccos}~(\text{tan}~\delta~~\text{tan}~\textit{φ}~-~\text{sin}~h~/~(\text{cos}~\delta~~\text{cos}~\textit{φ}))~~~~~\dot{\vee}\\ ~ & \tau~=~360° - \text{arccos}~(\text{tan}~\delta~~\text{tan}~\textit{φ}~-~\text{sin}~h~/~(\text{cos}~\delta~~\text{cos}~\textit{φ})) \end{array} (37) folgt aus (8). Die obere Gleichung gilt in der ersten Tageshälfte, die untere in der zweiten Tageshälfte.
Offenbar wächst \(~\tau(h)~\) im Tagesverlauf streng monoton, wenn \(~\delta~\) als konstant angenommen wird (was im Laufe eines Tages näherungsweise richtig ist).

\begin{array}{ll} \textbf{(38)} & \tau~=~\text{arccot}~(\text{cot}~A~~\text{sin}~\textit{φ}~-~\text{tan}~h~~\text{cos}~\textit{φ}~/~\text{sin}~A)~~~~~~\text{für}~~~~A \in (0°,~180°)\\ ~ & \tau~=~\text{arccot}~(\text{cot}~A~~\text{sin}~\textit{φ}~-~\text{tan}~h~~\text{cos}~\textit{φ}~/~\text{sin}~A) +180°~~~~~~\text{für}~~~~A \in (180°,~360°) \end{array} (38) folgt aus (11). Beachte Kasten unter (4). — (38) hat den Vorzug, dass hier \(~\tau~\) eineutig bestimmt wird, man also nicht wie bei (37) vorher wissen muss, ob es Vormittag oder Nachmittag ist.

\begin{array}{lll} \textbf{(39)} & A~\in (0°,~180°)~~\rightarrow~~~ & \tau~=~\text{arcsin}~(\text{cos}~h~~\text{sin}~A~/~\text{cos}~\delta)~~~~~~~\vee\\ ~ & ~ & \tau~=~180°-\text{arcsin}~(\text{cos}~h~~\text{sin}~A~/~\text{cos}~\delta)\\ ~ & A~\in (180°,~360°)~~\rightarrow~~~ & \tau~=~\text{arcsin}~(\text{cos}~h~~\text{sin}~A~/~\text{cos}~\delta)+ 360°~~~~~\vee\\ ~ & ~ & \tau~=~180°-\text{arcsin}~(\text{cos}~h~~\text{sin}~A~/~\text{cos}~\delta) \end{array} (39) folgt aus (7). In Beispiel 5 wird erklärt, welcher der beiden Werte für \(~\tau~\) in Frage kommt.

\begin{array}{ll} \textbf{(40)} & \text{Die Bestimmung von}~~\tau~~\text{mittels}~~\textit{φ},~~\delta~~\text{und}~~A~~\text{ist umständlicher, aber mit (10) möglich.}\\ ~ & \text{Man erhält eine Gleichung der Form}~~a~\text{cos}~\tau + b~\text{sin}~\tau = c~~,~\text{die mit sin}~\tau = \sqrt{1-\text{cos}^2~\tau}~~~\text{für}~~\tau \lt 180°\\ ~ & \text{und mit sin}~\tau = -\sqrt{1-\text{cos}^2~\tau}~~~\text{für}~~\tau \gt 180°~~\text{lösbar ist.} \end{array}

Wann geht die Sonne auf / unter ?\(~~~~~~h=0°\) \begin{array}{ll} \textbf{(41)} & \small{\text{Aufgang:}}\normalsize~~~~~\tau~=~\text{arccos}~(\text{tan}~\delta~~\text{tan}~\textit{φ})\\ ~ & \small{\text{Untergang:}}\normalsize~~~~~\tau~=~360°-\text{arccos}~(\text{tan}~\delta~~\text{tan}~\textit{φ}) \end{array} \begin{array}{ll} \textbf{(41a)} & \text{Aufgang vor}~~06:00~\text{Uhr}~~~\Leftrightarrow~~~\delta,~\textit{φ}~~\text{haben gleiches Vorzeichen} \end{array} (41) folgt aus (37).
(41) und (41a) sind nicht anwendbar im Polarsommer und -winter (d.h. wenn die Sonne den ganzen Tag über bzw. den ganzen Tag unter dem Horizont bleibt, denn dann ist \(~h \neq 0°\); siehe (50) und (63)). \begin{array}{ll} \textbf{(42)} & \small{\text{Aufgang:}}\normalsize~~~~~\tau~=~\text{arccot}~(\text{cot}~A~~\text{sin}~\textit{φ})\\ ~ & \small{\text{Untergang:}}\normalsize~~~~~\tau~=~\text{arccot}~(\text{cot}~A~~\text{sin}~\textit{φ}) + 180° \end{array} (42) folgt aus (38). Beachte Kasten unter (4).
(42) ist nicht anwendbar im Polarsommer und -winter (d.h. wenn die Sonne den ganzen Tag über bzw. den ganzen Tag unter dem Horizont bleibt, denn dann ist \(~h \neq 0°\); siehe (50) und (63)).

In (42) wächst (auf der Nordhalbkugel) bzw. fällt (auf der Südhalbkugel) die Aufgangszeit \(~\tau~\) streng monoton mit \(~A~\), mit dem Fixpunkt \(~(\tau,~A) = (90°,90°)~\) (dann ist nach (41) \(~\delta = 0°~\); dies harmoniert mit der Bemerkung unter Bild 8).

Wann steht die Sonne im Osten / Westen ?\(~~~~~~~A~=~90°~/~270°\) \begin{array}{ll} \textbf{(43)} & \small{\text{Osten:}}\normalsize~~~~~\tau~=~\text{arccos}~(-~\text{tan}~\delta~~\text{cot}~\textit{φ})\\ ~ & \small{\text{Westen:}}\normalsize~~~~~\tau~=~360°-\text{arccos}~(-~\text{tan}~\delta~~\text{cot}~\textit{φ}) \end{array} (43) folgt aus (10) und lässt sich nicht anwenden für \(~\textit{φ} = 0°\) (Äquator); siehe dazu (44).

(43) ist offenbar ebenfalls nicht anwendbar für \(~|~\text{tan}~\textit{φ}~| \lt |~\text{tan}~\delta~|~\), dies ist äquivalent zu \(~|~\textit{φ}~| \lt |~\delta~|\) und deckt die Fälle in (29) und Bild 7, Felder 2, 3 ab, in denen kein Ost- und kein Westpunkt existiert. \begin{array}{ll} \textbf{(43a)} & \text{Für}~~|~\textit{φ}~| \gt |~\delta~|~:~~~\text{Sonne steht nach}~~06:00~\text{Uhr}~~\text{im Osten}~~~\Leftrightarrow~~~\delta,~\textit{φ}~~\text{haben gleiches Vorzeichen} \end{array} \begin{array}{ll} \textbf{(44)}~~~\textit{φ} = 0°~~\text{(Äquator)} & ~~\small{\text{Osten:}}\normalsize~~~~~\delta~=~0°~~~\wedge~~~\tau~\in~(0°,~180°)\\ ~ & ~~\small{\text{Westen:}}\normalsize~~~~~\delta~=~0°~~~\wedge~~~\tau~\in~(180°,~360°) \end{array} (44) folgt aus (10) mit \(~0~=~\text{tan}~\delta~/~\text{sin}~\tau~\), siehe auch (36).

Beispiel 4 — zu (38)
\begin{array}{llll} \textit{φ} = -21° & h = 6° & A = 96° & \rightarrow~~~\tau \approx 93,5°\\ \textit{φ} = -21° & h = 6° & A = 264° & \rightarrow~~~\tau \approx 266,5° \end{array} Hier wurde eine Symmetrie gezeigt: Wenn die Werte für \(~A~\) symmetrisch zur Nord-Süd-Richtung liegen, dann liegen die Werte für \(~\tau~\) symmetrisch zum Mittag.

Beispiel 5 — zu (39)
\begin{array}{llll} \delta = -23° & h = 46° & A = 97° & \rightarrow~~~\tau_{~\small{2}\normalsize}~\approx~48,5°~~~~\tau_{~\small{3}\normalsize}~\approx~131,5° \end{array} → Die Bezeichnungen \(~\tau_{~\small{0}\normalsize}~\) und \(\tau_{~\small{1}\normalsize}~\) sind durch (29) / (30) bereits vergeben.
Um zu ermitteln, ob \(~\tau_{~\small{2}\normalsize}~\) oder \(~\tau_{~\small{3}\normalsize}~\) zutreffen, berechnen wir \(~\textit{φ}~\) mit (9) und \(~x=\text{sin}~\textit{φ}~\): \begin{array}{llll} \delta = -23° & h = 46° & A = 97° & \rightarrow~~~\textit{φ} \approx -25,9° \end{array} Dieses \(~\textit{φ}~\) setzen wir in (5) oder (6) zusammen mit \(~\tau_{~\small{2}\normalsize}~\) bzw. \(~\tau_{~\small{3}\normalsize}~\) ein. Nur \(~\tau_{~\small{3}\normalsize}~\) erfüllt diese Grundgleichungen. Also folgt: \begin{array}{llll} \delta = -23° & h = 46° & A = 97° & \rightarrow~~~\tau \approx 131,5° \end{array} Weiteres Beispiel zu (39): \begin{array}{llll} \delta = -23° & h = 0,4° & A = 97° & \rightarrow~~~\text{Keine Lösung (unzulässige Eingabewerte)} \end{array} Erklärung: \(~\text{sin}~\tau~=~\text{cos}~h~~\text{sin}~A~/~\text{cos}~\delta~\) hat keine Lösung für \(~\tau~\), wenn die rechte Seite nicht in \([-1,~1~]~\) ist.

Beispiel 6 — zu (40)
\begin{array}{lllll} \textit{φ} = 61° & \delta = 19°~\small{(\text{16. Mai, 29. Juli})}\normalsize & A = 284° & \rightarrow~~~\tau~\approx~275,3°~\small{(\text{18:21 Uhr})}\normalsize & \small{\text{siehe Feld 1 in Bild 7}}\normalsize\\ \textit{φ} = 6° & \delta = -9°~\small{(\text{26. Februar, 17. Oktober})}\normalsize & A = 164° & \rightarrow~~~\tau_{~\small{2}\normalsize}~\approx~0,9°~\small{(\text{00:04 Uhr})}\normalsize~~~~\tau_{~\small{3}\normalsize}~\approx~175,7°~\small{(\text{11:43 Uhr})}\normalsize & \small{\text{siehe Feld 2 in Bild 7}}\normalsize\\ \textit{φ} = 6° & \delta = -9°~\small{(\text{26. Februar, 17. Oktober})}\normalsize & A = 94° & \rightarrow~~~\text{Keine Lösung (unzulässige Eingabewerte)} & \small{\text{siehe Feld 2 in Bild 7}}\normalsize \end{array} Der Hinweis auf Feld 2 in Bild 7 wirft die Frage auf, bei welcher Himmelsrichtung \(~A~\) die Grenze zwischen zwei Lösungen und keiner Lösung für \(~\tau~\) liegt. Diese Grenze wird mit \(~A(\tau_{~\small{0}\normalsize})~\) in den eingerückten Formeln in (29) berechnet:

\(\tau_{~\small{0}\normalsize} \approx 48,4° ~~~~A(\tau_{~\small{0}\normalsize}) \approx 96,7°~~~~~~\tau_{~\small{1}\normalsize} \approx 311,6° ~~~~A(\tau_{~\small{1}\normalsize}) \approx 263,3°~\)

Interpretation: Die Sonne steht um Mitternacht im Süden \(~(180°)~\) und erreicht ihre größte östliche Richtung \(~96,7°~\) gegen \(~03:14~\text{Uhr}~\), läuft dann zurück über den Südpunkt (um \(~12:00~\text{Uhr}~\)) in Richtung Westen, mit der größten westlichen Richtung \(~263,3°\) gegen \(~20:46~\text{Uhr}~\), dann zurück nach Süden bis Mitternacht; siehe Feld 2 in Bild 7. – Da \(~A=94°\) nicht abgedeckt wird, gibt es dafür keine Lösung von (40).

Beispiel 7 — zu (41)

In Beispiel 1 wurde bereits eine Genauigkeitsabschätzung für ein Resultat dieser Formelsammlung gegeben. Wir wollen nun sehen, wie weit die mit (41) berechnete Zeit für den Sonnenaufgang mit gängigen Tabellenwerken oder astronomischen Jahrbüchern übereinstimmt. Es soll also der Effekt der vereinfachenden Annahmen unterhalb von (1) dargestellt werden.
\begin{array}{llll} \textit{φ} = 50° & \delta = 23°~\small{\text{(10./11. Juni, 3. Juli)}}\normalsize & \rightarrow & \small{\text{Sonnenaufgang (41) um}}\normalsize ~~\tau \approx 59,6°~\small{(\text{03:58 Uhr})}\normalsize\\ ~ & ~ & ~ & \small{\textcolor{orange}{\textit{Kosmos Himmelsjahr 2021:}~~\textbf{03:52}}}\normalsize\\ ~ & ~ & ~ & ~\\ \textit{φ} = 50° & \delta = -10,2°~\small{\text{(23. Februar, 20. Oktober)}}\normalsize & \rightarrow & \small{\text{Sonnenaufgang (41) um}}\normalsize ~~\tau \approx~102,4° \small{(\text{06:50 Uhr})}\normalsize\\ ~ & ~ & ~ & \small{\textcolor{orange}{\textit{Kosmos Himmelsjahr 2021:}~~\textbf{06:45}}}\normalsize \end{array} Die Abweichungen sind nicht unerheblich, lassen sich aber zum Teil erklären. Als "Sonnenaufgang" gilt das Erscheinen des oberen Sonnenrands am Horizont. Da in dieser Formelsammlung die Sonne als punktförmig angenommen wird, also nur ihr Mittelpunkt betrachtet wird, müssen zu den tabellarischen Werten ca. 2 Minuten addiert werden. Das Gleiche gilt für die Refraktion: Die Lufthülle der Erde lässt uns die Sonne weitere 2 Minuten früher sehen als theoretisch erwartet. So schrumpft die Differenz zwischen unseren Formelwerten und den Tabellenwerten auf ein vertretbares Maß.

Bestimmung der Deklination

\(\tau~\) Uhrzeit, \(~\textit{φ}~\) Breitengrad des Beobachters, \(~\delta~\) Deklination, \(h~\) Sonnenhöhe, \(~A~\) Himmelsrichtung der Sonne
\begin{array}{ll} \textbf{(45)} & \delta~=~\pm~\text{arccos}~(\text{cos}~h~~\text{sin}~A~/~\text{sin}~\tau) \end{array} (45) folgt aus (7) und lässt sich nicht anwenden für \(~\tau = 0°,~180°.~~~\text{"}\pm\text{"}~\) gehört zu zwei verschiedenen \(~\textit{φ}\). Beispiel 8 zeigt, welche Fälle vorkommen können.

\begin{array}{ll} \textbf{(46)} & \delta~=~\text{arcsin}~(\text{cos}~h~~\text{cos}~A~~\text{cos}~\textit{φ} + \text{sin}~h~~\text{sin}~\textit{φ}) \end{array} (46) folgt aus (9). – Daraus (oder aus (21b)) folgt für die Pole: \begin{array}{ll} \textbf{(46a)} & \textit{φ} = \pm~90°~~~\rightarrow~~~\delta~=~\pm~h\\ ~ & ~\\ \textbf{(47)} & \delta~=~\text{arctan}~(\text{cot}~A~~\text{sin}~\tau~/~\text{cos}~\textit{φ} - \text{cos}~\tau~~\text{tan}~\textit{φ}) \end{array} (47) folgt aus (10) und lässt sich nicht anwenden für \(~A = 0°,~180°\).

\begin{array}{ll} \textbf{(48)} & \text{Die Bestimmung von}~~\delta~~\text{mittels}~~\textit{φ},~~\tau~~\text{und}~~h~~\text{ist umständlicher, aber mit (8) möglich.}\\ ~ & \text{Man erhält eine Gleichung der Form}~~a~\text{cos}~\delta + b~\text{sin}~\delta = c~~,~\text{die mit cos}~\delta =\sqrt{1-\text{sin}^2~\delta}~~\text{lösbar ist.} \end{array}

Verwendung der Mittags- oder Mitternachtshöhe der Sonne\(~~~~~~\tau,~A~=~0°,~180°\) \begin{array}{llll} \textbf{(49)} & \tau=0°~~\small{\text{Mitternacht}}\normalsize ~~~ & \rightarrow~~~~\delta~=~-\textit{φ}\pm (h+90°) & \huge{_{\textbf{➘}}}\normalsize~~~~~~~\small{\text{" + " für}~~A=0°,~~\text{" – " für}~~A=180°~~~~(\text{siehe (12),}~~\textit{φ} \gt -\delta~~\text{bzw.}~~\textit{φ} \lt -\delta)}\normalsize\\ ~ & ~ & ~ & ~~~~~\small{\delta~~\text{kann keinen (nur bei nicht-empirischen Eingabewerten), einen oder zwei Werte annehmen.}}\normalsize\\ ~ & \tau=180°~~\small{\text{Mittag}}\normalsize ~~~ & \rightarrow~~~~\delta~=~\textit{φ}\pm (h-90°) & \huge{^{\textbf{➚}}}\normalsize~~~~~~~\small{\text{" + " für}~~A=180°,~~\text{" – " für}~~A=0°~~~~(\text{siehe (12),}~~\textit{φ} \gt \delta~~\text{bzw.}~~\textit{φ} \lt \delta)}\normalsize\\ ~ & ~ & ~ & ~\\ ~ & \small{\text{Daraus folgt:}} & ~ & ~\\ ~ & A = 0°~~\small{\text{Norden}}\normalsize & \rightarrow~~~\delta~=~90° \pm(\textit{φ}-h) & \huge{_{\textbf{➘}}}\normalsize~~~~~~~\small{\text{" + " für}~~\tau=180°~\wedge~h \neq 90°,~~\text{" – " für}~~\tau=0°~\wedge~h \neq -90°~~~~(\textit{φ} \lt \delta~~\text{bzw.}~~\textit{φ} \gt -\delta)}\normalsize\\ ~ & ~ & ~ & ~~~~~\small{\delta~~\text{kann keinen (nur bei nicht-empirischen Eingabewerten), einen oder zwei Werte annehmen.}}\normalsize\\ ~ & A = 180°~~\small{\text{Süden}}\normalsize & \rightarrow~~~\delta~=-90° \pm(\textit{φ}+h) & \huge{^{\textbf{➚}}}\normalsize~~~~~~~\small{\text{" + " für}~~\tau=180°~\wedge~h \neq 90°,~~\text{" – " für}~~\tau=0°~\wedge~h \neq -90°~~~~(\textit{φ} \gt \delta~~\text{bzw.}~~\textit{φ} \lt -\delta)}\normalsize \end{array} Die beiden ersten Formeln von (49) folgen aus (25); dabei ergibt sich genau ein Wert für \(~\delta~\), wenn die Klammern \(~= 0~\) werden – in diesem Fall gibt es keine Himmelsrichtung \(~A~\).

Für welche Deklinationen herrscht Polarsommer oder -winter ? \begin{array}{ll} \textbf{(50)} & \small{\text{Nordpolarsommer:}}\normalsize & \delta~\ge~90°-\textit{φ}\\ ~ & \small{\text{Nordpolarwinter:}}\normalsize & \delta~\le~\textit{φ}~-~90°\\ ~ & ~ & ~\\ ~ & \small{\text{Südpolarsommer:}}\normalsize & \delta~\le~-\textit{φ}~-~90°\\ ~ & \small{\text{Südpolarwinter:}}\normalsize & \delta~\ge~\textit{φ}~+~90° \end{array} (50) folgt aus (25) mit \(~h \ge 0°~\) oder \(~h \le 0°~\) und \(~\tau = 0°~\) oder \(~\tau = 180°\).

Beispiel 8 — zu (45)

Ohne eine Zwischenrechnung über \(~\textit{φ}~\) mit (11) kommt man hier nicht aus: \begin{array}{lllll} \tau = 100° & h = 14° & A = 96° & \rightarrow~~~\delta \approx\pm~11,5° & \textit{φ}_1 \approx 72,3°~~~\textit{φ}_2 \approx -26,8°\\ ~ & ~ & ~ & \rightarrow~~~\small{\text{Test mit (5), (6):}}\normalsize & \delta \approx 11,5°~~~\small{\text{für}}\normalsize~~~\textit{φ} \approx 72,3°~~~~~~~\delta \approx -11,5°~~~\small{\text{für}}\normalsize~~~\textit{φ} \approx -26,8°\\ ~ & ~ & ~ & ~ & ~\\ \tau = 250° & h = 2° & A = 296° & \rightarrow~~~\delta \approx\pm~17,1° & \textit{φ} \approx -43,5°\\ ~ & ~ & ~ & \rightarrow~~~\small{\text{Test mit (5), (6):}}\normalsize & \delta \approx 17,1°\\ ~ & ~ & ~ & ~ & ~\\ \tau = 96° & h = 22° & A = 112° & \rightarrow~~~\delta \approx\pm~30,2°~\huge{\text{↯}}\normalsize & \text{kommt real nicht vor}\\ ~ & ~ & ~ & ~ & ~\\ \tau = 204° & h = 22° & A = 222° & ~ & \text{keine Lösung, da das Argument des}~~\textit{arccos}~~\text{betragsmäßig}~\gt~1~\text{ist.} \end{array}

Beispiel 9 — zu (46) - (48)

Für beobachtete Eingabewerte erhält man mit (46) natürlich immer ein gültiges und eindeutiges \(~\delta~\). Dies gilt für beliebige Eingabewerte nur dann, wenn das Argument des arcsin betragsmäßig \(~\le~1~\) ist und \(~\delta \in [-23,44°,~23,44°]\).

Für beobachtete Eingabewerte erhält man mit (47) natürlich immer ein gültiges und eindeutiges \(~\delta~\). Dies gilt für beliebige Eingabewerte nur dann, wenn \(~\delta \in [-23,44°,~23,44°]\), siehe auch Beispiel 12.

Zu (48) siehe Beispiel 3.

Bestimmung des Breitengrades

\(\tau~\) Uhrzeit, \(~\textit{φ}~\) Breitengrad des Beobachters, \(~\delta~\) Deklination, \(h~\) Sonnenhöhe, \(~A~\) Himmelsrichtung der Sonne
\begin{array}{ll} \textbf{(51)} & \text{Die Bestimmung von}~~\textit{φ}~~\text{mit (8) - (11) ist mit Gleichungen der Form}~~a~\text{cos}~\textit{φ} + b~\text{sin}~\textit{φ} = c~~\text{und cos}~\textit{φ} =\sqrt{1-\text{sin}^2~\textit{φ}}~~\text{möglich.} \end{array}

Verwendung des Sonnenaufgangs /-untergangs\(~~~~~~h~=~0°\) \begin{array}{ll} \textbf{(52)} & \textit{φ}~=~\text{arctan}~(\text{cot}~\delta~~\text{cos}~\tau) \end{array} (52) folgt aus (8) und lässt sich nicht anwenden für \(~\delta = 0°\).

\begin{array}{ll} \textbf{(53)} & \textit{φ}~=~\pm~\text{arccos}~(\text{sin}~\delta~/~\text{cos}~A) \end{array} (53) folgt aus (9) und lässt sich nicht anwenden für \(~A = 90°,~270°\), und für \(~\delta~=~0°\).
Es gelten immer beide Vorzeichen für \(~\textit{φ}~\).
Man beachte, dass aus (35) folgt:
Sonnenaufgang: \(~~\delta~\gt 0°~~~\Leftrightarrow~~~A~\lt~90°\)
Sonnenuntergang: \(~~\delta~\gt 0°~~~\Leftrightarrow~~~A~\gt~270°\)

\begin{array}{ll} \textbf{(54)} & \textit{φ}~=~\text{arcsin}~(\text{cot}~\tau~/~\text{cot}~A) \end{array} (54) folgt aus (11) und lässt sich nicht anwenden für \(~\tau,~A = 0°,~180°\), und für \(~A = 90°\).

Verwendung markanter Uhrzeiten \begin{array}{llll} \textbf{(55)} & \tau=0°~~\small{\text{Mitternacht}}\normalsize ~~~ & \rightarrow~~~~\textit{φ}~=~\pm (h+90°)-\delta & ~~~~~~~\small{\text{" + " für}~~A=0°,~~\text{" – " für}~~A=180°~~~~(\textit{φ} \gt -\delta~~\text{bzw.}~~\textit{φ} \lt -\delta)}\normalsize \end{array} (55) folgt aus (49). \(~\textit{φ}~\) kann keinen (nur bei nicht-empirischen Eingabewerten), einen oder zwei Werte annehmen.
Genau ein Wert für \(~\delta~\) ergibt sich, wenn die Klammer \(~= 0~\) wird – in diesem Fall gibt es keine Himmelsrichtung \(~A~\).

\begin{array}{llll} \textbf{(56)} & \tau=180°~~\small{\text{Mittag}}\normalsize ~~~ & \rightarrow~~~~\textit{φ}~=~\pm (h-90°)+\delta & ~~~~~~~\small{\text{" + " für}~~A=0°,~~\text{" – " für}~~A=180°~~~~(\textit{φ} \lt \delta~~\text{bzw.}~~\textit{φ} \gt \delta)}\normalsize \end{array} (56) folgt aus (49). \(~\textit{φ}~\) kann keinen (nur bei nicht-empirischen Eingabewerten), einen oder zwei Werte annehmen.
Genau ein Wert für \(~\delta~\) ergibt sich, wenn die Klammer \(~= 0~\) wird – in diesem Fall gibt es keine Himmelsrichtung \(~A~\).

\begin{array}{lll} \textbf{(57)} & \tau=90°/270°~~~ & \rightarrow~~~~\textit{φ}~=~\text{arcsin}~(\text{sin}~h~/~\text{sin}~\delta) \end{array} (57) folgt aus (8).

\begin{array}{lll} \textbf{(58)} & \tau=90°~~\wedge~~\text{cot}~\delta~~\text{cot}~A~\gt~0~~ & \rightarrow~~~~\textit{φ}~=~\pm~\text{arccos}~(\text{cot}~\delta~~\text{cot}~A) \end{array} (58) folgt aus (10) und lässt sich nicht anwenden für \(~\delta=0°\). Man beachte \(~A \lt 180°\).

\begin{array}{lll} \textbf{(59)} & \tau=270°~~\wedge~~\text{cot}~\delta~~\text{cot}~A~\lt~0~~ & \rightarrow~~~~\textit{φ}~=~\pm~\text{arccos}~(-~\text{cot}~\delta~~\text{cot}~A) \end{array} (59) folgt aus (10) und lässt sich nicht anwenden für \(~\delta=0°\). Man beachte \(~A \gt 180°\).

\begin{array}{lll} \textbf{(60)} & \tau=90°/270°~~~ & \rightarrow~~~~\textit{φ}~=~\text{arctan}~(\text{tan}~h~/~\text{cos}~A) \end{array} (60) folgt aus (11).

Verwendung der Himmelsrichtung Norden / Süden \begin{array}{llll} \textbf{(61)} & A=0°~~~ & \rightarrow~~~~\textit{φ}~=~\pm~(90°-\delta)+h & ~~~~~~~\small{\text{" + " für}~~\tau=0°~\wedge~h \neq -90°,~~\text{" – " für}~~\tau=180°~\wedge~h \neq 90°~~~~(\textit{φ} \gt -\delta~~\text{bzw.}~~\textit{φ} \lt \delta)}\normalsize\\ ~ & ~ & ~ & ~\\ \textbf{(62)} & A=180°~~~ & \rightarrow~~~~\textit{φ}~=~\pm~(90°+\delta)-h & ~~~~~~~\small{\text{" + " für}~~\tau=180°~\wedge~h \neq 90°,~~\text{" – " für}~~\tau=0°~\wedge~h \neq -90°~~~~(\textit{φ} \gt \delta~~\text{bzw.}~~\textit{φ} \lt -\delta)}\normalsize \end{array} (61) und (62) folgen aus (55) und (56).

In welchen Breiten herrscht Polarsommer oder -winter ? \begin{array}{ll} \textbf{(63)} & \small{\text{Nordpolarsommer:}}\normalsize & \textit{φ}~\ge~90°-\delta\\ ~ & \small{\text{Nordpolarwinter:}}\normalsize & \textit{φ}~\ge~90°+\delta\\ ~ & ~ & ~\\ ~ & \small{\text{Südpolarsommer:}}\normalsize & \textit{φ}~\le~-\delta~-~90°\\ ~ & \small{\text{Südpolarwinter:}}\normalsize & \textit{φ}~\le~\delta~-~90° \end{array} (63) folgt aus (50).

Beispiel 10 — zu (51)

Beispiel 2 verwendet (8).

Beispiel 5 verwendet (9).

Beispiel 11 — zu (51)

Nun soll \(~\textit{φ}~\) mit (10) berechnet werden: \begin{array}{llll} \delta = 19° & \tau = 184° & A = 200° & \rightarrow~~~~\textit{φ} \approx 29,5°\\ ~ & ~ & ~ & ~\\ \delta = 17,1° & \tau = 93,5° & A = 74,5° & \rightarrow~~~~\textit{φ}_1 \approx 16,8°~~~~\textit{φ}_2 \approx -39,3°\\ ~ & ~ & A = 70° & \rightarrow~~~~\text{keine Lösung} \end{array} Diese drei Beispielrechnungen sollen illustriert werden durch die entsprechenden Graphen in Bild 10. Dort wird \(~A~\) in Abhängigkeit von \(~\textit{φ}~\) abgetragen.

A(phi)

Bild 10 Links \(~\delta = 19°,~\tau = 184°~\); rechts \(~\delta = 17,1°,~\tau = 93,5°\)

Beispiel 12 — zu (51)

Nun soll \(~\textit{φ}~\) mit (11) berechnet werden (und zur Überprüfung \(~\delta~\) mit (47)): \begin{array}{lllll} \tau = 82° & h = 6,7° & A = 81° & \rightarrow~~~~\textit{φ} \approx 82,1°~~\small{(~\delta \approx 7,9°)}\normalsize & ~\\ ~ & ~ & ~ & ~ & ~\\ \tau = 173° & h = 76,7° & A = 150° & \rightarrow~~~~\textit{φ}_1 \approx 31°~~\small{(~\delta_1 \approx 19,3°)}\normalsize & ~\textit{φ}_2 \approx -7,9°~~\small{(~\delta_2 \approx -19,3°)}\normalsize\\ ~ & ~ & ~ & ~ & ~\\ \tau = 246° & h = 27° & A = 261° & \rightarrow~~~~\textit{φ}_1 \approx 51,5°~~\small{(~\delta_1 \approx 15,6°)}\normalsize & ~\textit{φ}_2 \approx -17,3°~~\small{(~\delta_2 \approx -15,6°)}\normalsize\\ ~ & ~ & A = 244° & \rightarrow~~~~\text{keine Lösung, nach Probe mit}~~\delta~\text{!} & ~ \end{array} Das letzte Beispiel zeigt die Berechtigung der Warnung im orangenen Kasten oberhalb von (5) auf. Mit (11) erhält man \(~\textit{φ} \approx -12,8°\) und hat dabei aber nicht berücksichtigt, dass es sich um Eingabewerte handeln könnte, die in der Realität nicht vorkommen. In der Tat berechnet man mit (47) \(~\delta \approx -28,8°\).

Beispiel 13 — zu (54) \begin{array}{lll} \tau = 79° & A = 75° & \rightarrow~~~~\textit{φ} \approx 46,5°~~\small{(~\delta \approx 10,3°)}\normalsize\\ ~ & ~ & ~\\ \tau = 279° & A = 306° & \rightarrow~~~~\text{keine Lösung, nach Probe mit}~~\delta~\text{!} \end{array} Man kann also seinen eigenen Breitengrad und die Deklination berechnen, wenn man bei Sonnenaufgang oder -untergang Uhrzeit und Himmelsrichtung festhält. – Wie in Beispiel 12, so ist auch hier Vorsicht angebracht, wenn die Eingabewerte nicht aus Beobachtungen stammen. Mit (54) erhält man im unteren Beispiel \(~\textit{φ} \approx 12,6°\), aber \(~\delta \approx 35°\).

Kommentare sind willkommen: E-Mail

Kategorie: Geomathematik

Stand 2021-08-09

Manfred Börgens | Zur Leitseite