Manfred Boergens

MB Matheblog # 21

Inhalt Blog
voriger Eintrag nächster Eintrag

zur Leitseite
Index der gesamten Website

2022-09-06

Sonnenuhren Teil 4

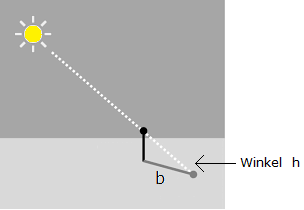
Gnomon Kommentare sind willkommen.

Eine besonders einfache Sonnenuhr hat einen senkrechten Schattenstab auf einem ebenen Untergrund. Der Stab wird als Gnomon bezeichnet; er wurde schon im Altertum zur Beobachtung geo-astronomischer Phänomene verwendet und geht bis auf die Babylonier zurück. Mit dem Gnomon wurden beispielsweise die Nordrichtung, der Mittagszeitpunkt, die geographische Breite sowie das Datum der Sonnenwenden und der Äquinoktien bestimmt. Auf die Funktion als Uhr werden wir noch zurückkommen.

"Gnomon" hat auch andere Bedeutungen, u.a. generell als schattenwerfender Stab für Sonnenuhren, der nicht notwendigerweise senkrecht stehen muss. Wir wollen hier nur vom senkrechten Gnomon sprechen und diesen Begriff sowohl für den Stab als auch für das gesamte Messinstrument incl. Winkelmessung und Messung der Schattenlänge verwenden.

In Bild 1 zeigt schematisch die Funktion eines Gnomons. Unmittelbar abzulesen sind die Länge und die Himmelsrichtung des Schattens; aus der Schattenlänge lässt sich der Höhenwinkel der Sonne berechnen.

Gnomon

Bild 1 Gnomon Copyright Mark Carlotto, researchgate

Im ersten Teil dieses Beitrags gehen wir rein mathematisch vor. Es wird gezeigt, wie man aus der Länge und der Himmelsrichtung des Schattens die Uhrzeit und die Deklination der Sonne (und damit das Datum) berechnen kann. Im zweiten Teil soll eine Gnomon-Sonnenuhr konstruiert werden, die eine direkte Ablesung von Uhrzeit und Deklination durch Markierungen auf dem Boden ermöglicht.

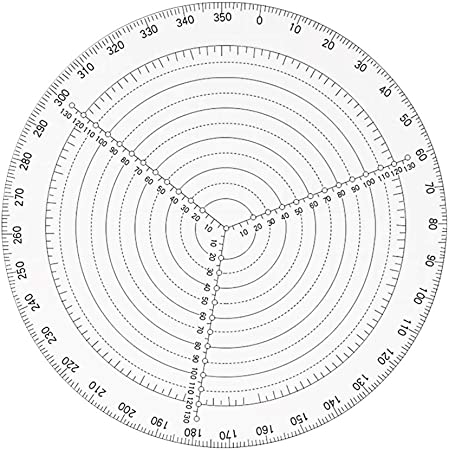
Zunächst also die "Taschenrechner-Aufgabe". Länge und Winkel des Schattens lassen sich z.B. leicht mit Hilfe eines Winkelmessers wie in Bild 2 feststellen, der waagerecht auf dem Boden liegt; der Gnomon steht dann senkrecht auf dem Mittelpunkt des Kreises.

Bild 2 Copyright Arvavolet (Hersteller)

Der Einfachheit halber wollen wir die Höhe des Gnomons als zu 1 normiert annehmen. Den Winkelmesser wollen wir so orientieren, dass der Schatten auf 0° fällt, wenn er genau nach Süden zeigt. Tabelle 1 zeigt die vier Haupthimmelsrichtungen:

Schatten fällt auf	Richtung des Schattens	Richtung der Sonne	Wann sichtbar? (Festes `φ, δ` `∈[-23,44°,` `23,44°])`	Wo sichtbar? (Festes `δ`)
`0°`	`Süd`	`Nord`	mittags für `δ` `∈(φ,` `φ+90°]` mitternachts für `δ` `≥90°-φ` (nur im Nordpolarsommer, → Formel (50))	`φ` `∈[δ-90°,` `δ) φ` `≥` `90°-δ` (→ Formel (63))
`90°`	`West`	`Ost`	morgens im Sommerhalbjahr	`φ` mit gleichem Vorzeichen wie `δ`
`180°`	`Nord`	`Süd`	mittags für `δ` `∈[φ-90°,` `φ)` mitternachts für `δ` `≤-φ-90°` (nur im Südpolarsommer, → Formel (50))	`φ` `∈(δ,` `δ+90°]``φ` `≤` `-δ-90°` (→ Formel (63))
`270°`	`Ost`	`West`	abends im Sommerhalbjahr	`φ` mit gleichem Vorzeichen wie `δ`

Tabelle 1 φ Breitengrad, δ Deklination der Sonne
Schwarz: Nördliche gemäßigte Breiten
Sommerhalbjahr: δ ≥ 0° auf Nordhalbkugel, δ ≤ 0° auf Südhalbkugel
Die Links (50) und (63) verweisen auf die Geo-astronomische Formelsammlung auf dieser Website.

Nun zur Berechnung von τ und δ .

(I)

Stabhöhe = 1 Eingabe φ : Breitengrad A : Himmelsrichtung (Azimut, wie in Tabelle 1) b : Länge des Stabschattens Ausgabe τ : Uhrzeit δ : Deklination der Sonne (Umrechnung in ein Datum siehe → Tabelle) h : Höhenwinkel der Sonne τ = arccot(cot A sin φ - tan h cos φ / sin A) in Grad, siehe (38) +180° für A > 180° δ = arcsin(cos h cos A cos φ + sin h sin φ) siehe (46) Mit h = arccot b (siehe Bild 1) erhalten wir: τ = arccot(cot A sin φ - cos φ / (b·sin A)) / 15 in Stunden umgerechnet; 1h = 15° +12 für A > 180° δ = arcsin(cos(arccot b) cos A cos φ + sin(arccot b) sin φ)
Umrechnung in ein Datum siehe → Tabelle.

Die letzten (fetten) Zeilen von (1) sind das zentrale Ergebnis für den ersten Teil dieses Beitrags: Nur aus der Himmelsrichtung der Sonne und der Schattenlänge lassen sich Uhrzeit und Datum berechnen – sofern man weiß, auf welchem Breitengrad man sich befindet. Die Berechnung beruht auf dem vereinfachten Modell, das in der Formelsammlung erklärt wird. Für eine andere Stabhöhe s (statt 1) nimmt man b/s statt b .

Beispiele:

`φ`	`A`	`b`	`τ`	`δ`	`Datum ca.`
`50°`	`195°`	`0,75`	`12:37`	`13,9°`	`28.4. 16.8.`
`71°`	`109°`	`1,7`	`07:51`	`22,8°`	`8.6. 5.7.`
`19°`	`153,3°`	`0,53`	`11:11`	`-6,2°`	`5.3. 9.10.`
`-31°`	`93°`	`1,05`	`08:33`	`-22,8°`	`9.12. 4.1.`

Tabelle 2

Nun zum zweiten Teil: Wie konstruiert man eine Gnomon-Sonnenuhr? Im ersten Teil haben wir gesehen, dass die Himmelsrichtung und die Länge des Stabschattens ausreichen, um die Uhrzeit zu bestimmen, und die Deklination der Sonne wird noch mitgeliefert. Bei gewöhnlichen Sonnenuhren dient der Schatten als Uhrzeiger; aber es ist schon seit alters her bekannt und lässt sich auch leicht empirisch überprüfen, dass der Schatten des Gnomons zu verschiedenen Zeiten des Jahres verschiedene Winkel im Tagesverlauf überstreicht. Da wir im ersten Teil die Schattenlänge als Eingabewert verwendet haben, liegt es nahe, dass die Spitze des Schattens zur Ablesung der Uhrzeit verwendet werden kann. Die Bahn der Schattenspitze werden wir berechnen, um zu sehen, ob sie dazu taugt.

In der Literatur zum Gnomon begegnet uns eine Merkwürdigkeit, die uns entmutigen könnte. An verschiedenen Stellen wird dem Gnomon die Eignung als Sonnenuhr abgesprochen. Hier ein paar Zitate (Quellen am Seitenende):

In gewisser Hinsicht kann der Gnomon als Vorläufer der Sonnenuhr gelten. [2, S. 356-358], [3, S. 248-252]

... ist der Gnomon eine schlechte Sonnenuhr. [4]

Wenn es auch anfangs nur ein bescheidener Schattenstab (Gnomon) war, der in die Erde gesteckt wurde, kann man diesen als den Vorläufer der Sonnenuhr sowie als das erste astronomische Instrument bezeichnen. ... Es musste stets das betreffende Datum in die Zeitablesung mit einbezogen werden – eine recht umständliche Prozedur. [1]

Aber man sollte sich davon nicht abhalten lassen und dem Gnomon eine Chance geben. Denn über kurz oder lang stößt jeder Sonnenuhren-Freund auf den Obelisken auf der Halde Hoheward im Süden von Herten, siehe Bild 3. Wir sehen dort die Schattenspitze eines Gnomons (der hier ein Obelisk von 8,50 m Höhe ist) über ein Zifferblatt laufen, das zwar anders, aber auch nicht viel komplizierter als bei anderen Sonnenuhren aussieht.

Obelisk Herten

Bild 3 Gnomon-Sonnenuhr auf der Halde Hoheward. Die Linien auf dem Boden sind exakt für den Breitengrad 51°34' Nord gezeichnet. Copyright

Nun zu den Berechnungen. Die Zahlen in Klammern hinter den Formeln für A und h verweisen auf die Formelsammlung auf dieser Website.

(II) Erste Vorbereitung für das Zifferblatt

Stabhöhe = 1 Eingabe φ : Breitengrad τ : Tageszeit in Grad (1h = 15°, gerechnet seit Mitternacht δ : Deklination der Sonne (Umrechnung aus einem Datum siehe → Tabelle) Ausgabe A : Himmelsrichtung des Stabschattens (Azimut, wie in Tabelle 1) h : Höhenwinkel der Sonne A = arccot(cot τ sin φ + tan δ cos φ / sin τ) in Grad, siehe (27) +180° für τ > 180° h = arcsin(-cos δ cos τ cos φ + sin δ sin φ) siehe (21)

(III) Zweite Vorbereitung für das Zifferblatt: Polarkoordinaten und kartesische Koordinaten

Mit (I) gilt für b (Länge des Stabschattens, siehe Bild 1): b = cot h Koordinaten für die Schattenspitze: (b, A) Polarkoordinaten (b cos A, b sin A) kartesische Koordinaten

(IV) Kurven auf dem Zifferblatt

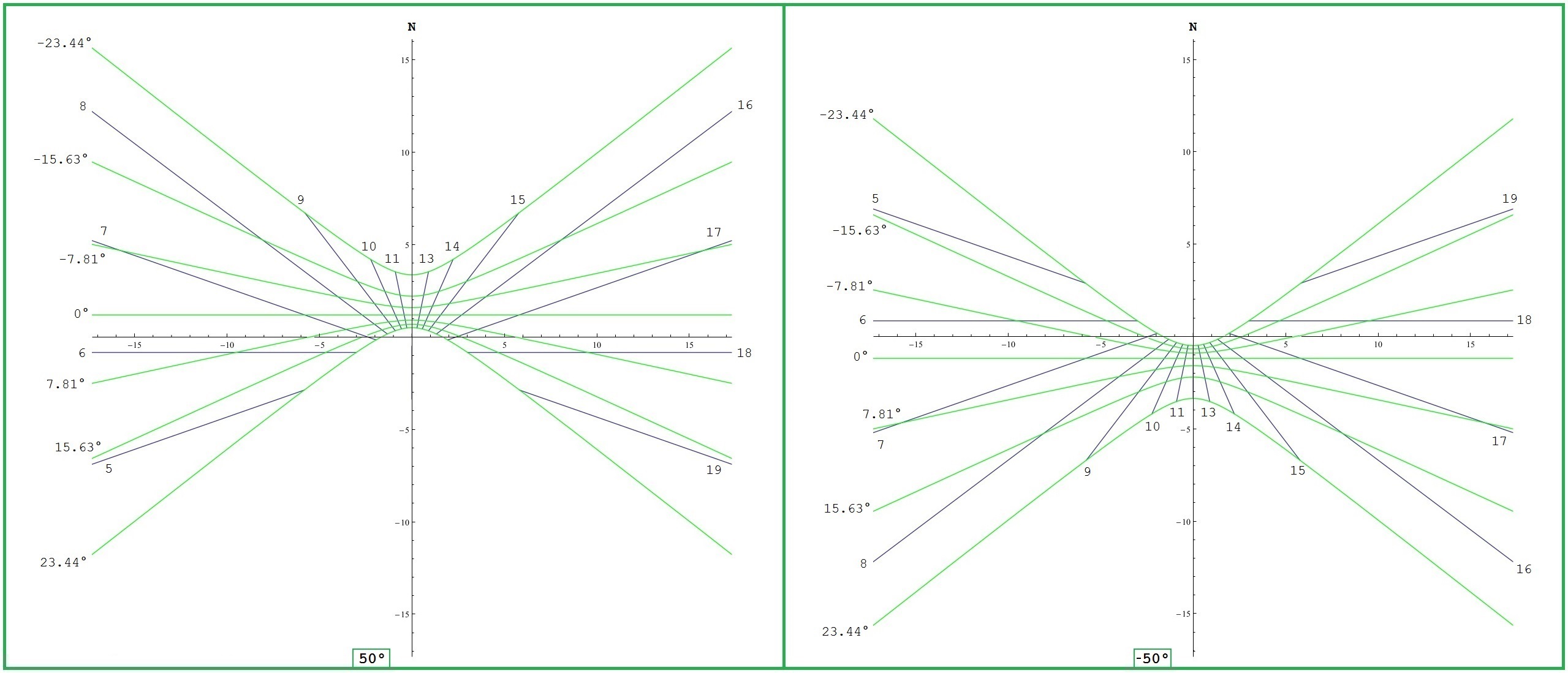
Mit b und A aus (II) und (III) erhalten wir für festes φ : (b cos A, b sin A) ist für festes δ eine Parameterkurve mit τ als unabhängiger Variable. Diese Kurve zeigt für eine bestimmte Deklination δ an, welchen Weg die Schattenspitze im Laufe eines Tages nimmt. Das gilt nur näherungsweise, da sich die Deklination im Laufe eines Tages geringfügig verändert. – In Bild 3 erkennt man diese Kurven als die sieben Linien, die vom oberen Rand zum unteren Rand laufen; die linke Kurve steht für den Winteranfang mit δ = -23,44°, wenn die Schatten am längsten sind.(b cos A, b sin A) ist für festes τ eine Parameterkurve mit δ als unabhängiger Variable. Diese Kurve zeigt für eine bestimmte Uhrzeit τ an, auf welchem Weg die Schattenspitze im Jahresverlauf wandert. – In Bild 3 sind das die Strecken, die fächerförmig auf einen Punkt hinter dem Gnomon zulaufen. Insgesamt sehen wir dort 11 dieser Strecken; sie stehen für die vollen Stunden von 07:00 Uhr bis 17:00 Uhr.

Mit (IV) wissen wir nun, welchen mathematischen Funktionen die Linien auf dem Boden des Gnomons auf der Hoheward folgen. Für beliebige Breitengrade können wir mit (II) - (IV) Gnomon-Sonnenuhren herstellen. Wichtig ist dabei, dass nur die Schattenspitze die Uhrzeit und die Deklination (und damit das ungefähre Datum) anzeigt, d.h. die Schattenlinie ist ungeeignet als Uhrzeiger, der ein Zifferblatt überstreicht.

Es folgen in Bild 4 zwei erste Beispiele für die Parameterkurven. Die Grad-Angaben stehen für die Deklinationen δ , die natürlichen Zahlen für die Uhrzeiten τ (volle Stunden).

50 -50 Grad

Bild 4 φ = 50° und φ = -50°;
alle Deklinationen kommen vor.

Es ist hilfreich bei der Darstellung der Graphen der Parameterfunktionen in (IV), wenn man weiß, für welche Paare (δ,τ) auf einem bestimmten Breitengrad φ die Sonne über dem Horizont steht – nur dann kann man eine Sonnenuhr gebrauchen. So werden z.B. auf dem 50. Breitengrad sehr frühe Uhrzeiten τ nur bei großen Deklinationen δ vorkommen. Wir werden uns also nun den Eigenschaften der δ-Linien und der τ-Linien widmen, wie wir sie in den Bildern 3 und 4 sehen.

Zeichnet man mit (IV) Linien wie in Bild 4, so fallen verschiedene Phänomene auf. Eine δ-Linie hat genau dann eine endliche Länge, wenn die Sonne in dieser Deklination ganztägig über dem Horizont steht. Eine τ-Linie hat genau dann eine endliche Länge, wenn die Sonne zu dieser Tageszeit ganzjährig über dem Horizont steht. Beides leuchtet ein, denn bei Sonnenauf- und -untergang ist der Stabschatten unendlich lang. Die Linien müssen in diesem Fall bei der Konstruktion der Gnomon-Sonnenuhr abgeschnitten werden.

Die 0°-Linie erweist sich als Gerade und jede τ-Linie als Strecke oder Halbgerade.

Im Folgenden wird berechnet, welche δ-Linien und τ-Linien auf einem bestimmten Breitengrad überhaupt vorkommen, welche von ihnen endliche Länge haben und welche Definitionsbereiche der Parameterkurven in (IV) für die Zeichnung der Linien gelten.

(V) Welche δ-Linien kann man aufzeichnen?

Alle δ entfallen, für die die Sonne ganztägig unter oder auf dem Horizont steht. Nach (50) ist das nur in der Nordpolarregion für δ ≤ φ - 90° und in der Südpolarregion für δ ≥ φ + 90° der Fall. Also gilt für δ ∈ [-23,44°, 23,44°]: • δ-Linien Nordhalbkugel: δ > φ - 90° • δ-Linien Südhalbkugel: δ < φ + 90°

(VI) Welche τ-Linien kann man aufzeichnen?

Für den Sonnenaufgang τ₀ gilt nach (41), außer an den Polen: cos τ₀ = tan δ tan φ Auf der Nordhalbkugel wird somit das früheste τ₀ für δ = 23,44° erreicht. Das kann aber nur gelten, wenn φ < 66,56°, da cos τ₀ ≤ 1; ansonsten gibt es keinen Sonnenaufgang (Nordpolarsommer). • τ-Linien Nordhalbkugel: φ < 66,56°: τ ∈ (arccos(tan 23,44° tan φ), 360° - arccos(tan 23,44° tan φ)) φ = 66,56°: Alle τ-Linien kommen vor, außer für τ = 0°. φ > 66,56°: Alle τ-Linien kommen vor.Dies gilt auch für den Nordpol. Aus Symmetriegründen erhalten wir: • τ-Linien Südhalbkugel: φ > -66,56°: τ ∈ (arccos(tan -23,44° tan φ), 360° - arccos(tan -23,44° tan φ)) φ = -66,56°: Alle τ-Linien kommen vor, außer für τ = 0°. φ < -66,56°: Alle τ-Linien kommen vor.

(VII) Welche δ-Linien sind endlich?

Das kann nur vorkommen, wenn für eine Deklination δ die Sonne ganztägig über dem Horizont steht. Nach (50) gilt für δ ∈ [-23,44°, 23,44°]: • Endliche δ-Linien Nordhalbkugel: δ > 90° - φ • Endliche δ-Linien Südhalbkugel: δ < -90° - φ

(VIII) Welche τ-Linien sind endlich?

Das kann nur vorkommen, wenn der Sonnenaufgang ganzjährig früher als τ liegt. Dies ist auf der Nordhalbkugel gleichbedeutend damit, dass für δ=-23,44° die Sonne zum Zeitpunkt τ über dem Horizont steht. Analog zu (VI) gilt dann für denn Sonnenaufgang τ₀: cos τ₀ = tan -23,44° tan φ ≥ -1; sinnvoll nur für φ < 66,56°; ansonsten gibt es keinen Sonnenaufgang (Nordpolarwinter). • Endliche τ-Linien Nordhalbkugel: φ < 66,56° ∧ τ ∈ (arccos(tan -23,44° tan φ), 360° - arccos(tan -23,44° tan φ))Aus Symmetriegründen erhalten wir: • Endliche τ-Linien Südhalbkugel: φ > -66,56° ∧ τ ∈ (arccos(tan 23,44° tan φ), 360° - arccos(tan 23,44° tan φ))

(IX) Definitionsbereich für die δ-Linien

Wir halten in der Parameterdarstellung (b cos A, b sin A) in (IV) eine Deklination δ aus (V) fest (und bestimmen diejenigen Tageszeiten τ, bei denen die Sonne auf dem Breitengrad φ über dem Horizont steht. Nach (50) steht die Sonne im Nordpolarsommer bei δ ≥ 90° - φ ganztägig über dem Horizont (bei "=" um Mitternacht auf dem Horizont). Ansonsten berechnet man die Zeitpunkte τ₀ und τ₁ für Sonnenauf- und -untergang nach (41) wie folgt: τ₀ = arccos(tan δ tan φ) τ₁ = 360° - arccos(tan δ tan φ) • Definitionsbereich für δ-Linien Nordhalbkugel: δ < 90° - φ : τ ∈ (τ₀, τ₁) δ ≥ 90° - φ : τ ∈ [0°, 360°) 0° entfällt bei "=". Aus Symmetriegründen erhalten wir: • Definitionsbereich für δ-Linien Südhalbkugel: δ > -90° - φ : τ ∈ (τ₀, τ₁) δ ≤ -90° - φ : τ ∈ [0°, 360°) 0° entfällt bei "=".

(X)   Definitionsbereich für die τ-Linien

Wir halten in der Parameterdarstellung (b cos A, b sin A) in (IV) eine Tageszeit τ aus (VI) fest und bestimmen diejenigen Deklinationen δ, bei denen die Sonne auf dem Breitengrad φ über dem Horizont steht. φ = 0° (Äquator) und φ = ±90° (Pole) werden weiter unten gesondert behandelt.Auf dem Breitengrad φ geht für δ = arctan(cos τ cot φ) die Sonne zur Uhrzeit τ auf bzw. unter (siehe (8), mit h = 0). Auf der Nordhalbkugel steht für alle größeren Deklinationen die Sonne höher am Himmel. Da nur δ ∈ [-23,44°, 23,44°] vorkommt, ist die Untergrenze des Definitionsintervalls gleich max{-23,44°, arctan(cos τ cot φ)}.

• Definitionsbereich für τ-Linien Nordhalbkugel:     cos τ < tan -23,44° tan φ : δ ∈ [-23,44°, 23,44°]
    Das sind genau diejenigen τ, die nach (VIII) zu einer endlichen τ-Linie gehören.

    cos τ ≥ tan -23,44° tan φ : δ ∈ (arctan(cos τ cot φ), 23,44°]

Aus Symmetriegründen erhalten wir:

• Definitionsbereich für τ-Linien Südhalbkugel:     cos τ < tan 23,44° tan φ : δ ∈ [-23,44°, 23,44°]
    Das sind genau diejenigen τ, die nach (VIII) zu einer endlichen τ-Linie gehören.

    cos τ ≥ tan 23,44° tan φ : δ ∈ [-23,44°, arctan(cos τ cot φ))

• Äquator: Aus (VI) folgt cos τ < 0. Nach (8) mit φ = 0° und h > 0° gilt dann, dass alle δ erlaubt sind: δ ∈ [-23,44°, 23,44°]

• Nordpol: Aus h > 0 folgt mit (8), dass δ > 0 : δ ∈ (0°, 23,44°]

• Südpol: Aus h > 0 folgt mit (8), dass δ < 0 : δ ∈ [-23,44°, 0°)

Beispiele:

`φ`	`δ (≤` `23,44°)`	endl. `δ-`Linien	Def.ber. `δ-`Linien	`τ D₁` `=`	endl. `τ-`Linien `D₂` `=`	Def.ber. `τ-`Linien `(δ` `≤` `23,44°)` `τ` `∈` `D₂:` `δ` `≥` `-23,44° τ` `Rd.pkt.von` `D₂:` `δ` `>` `-23,44° τ` `∈` `D₁∖D₂:`
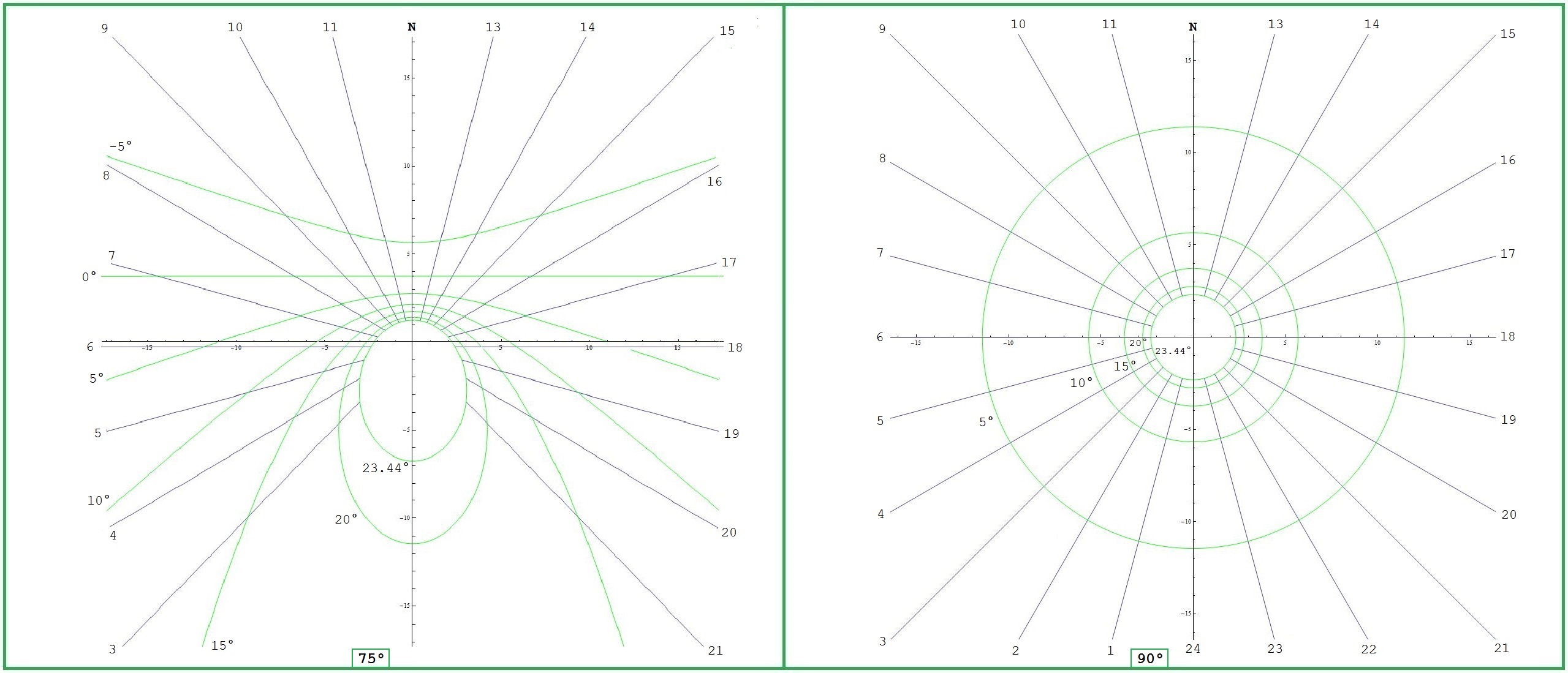
`90°`	`>` `0°`	`>` `0°`	`τ` `∈` `[0°,` `360°)` `=` `[00:00,` `24:00)`	`[0°,` `360°) =` `[00:00,` `24:00)`	`—`	`δ` `>` `0°`	Nordpol siehe Bild 6
`75°`	`>` `-15°`	`>` `15°`	`δ` `>` `15°: τ` `∈` `[0°,` `360°)` `=` `[00:00,` `24:00) δ` `=` `15°: τ` `∈` `(0°,` `360°)` `=` `(00:00,` `24:00) δ` `<` `15°: τ` `∈` `(arccos(3,732·tan` `δ), 360°-` `arccos(3,732·tan` `δ))`	`[0°,` `360°) =` `[00:00,` `24:00)`	`—`	`δ` `>` `arctan(0,268·cos` `τ)`	`2` `+` `√3 ≈ 3,732 2` `-` `√3 ≈ 0,268` siehe Bild 6
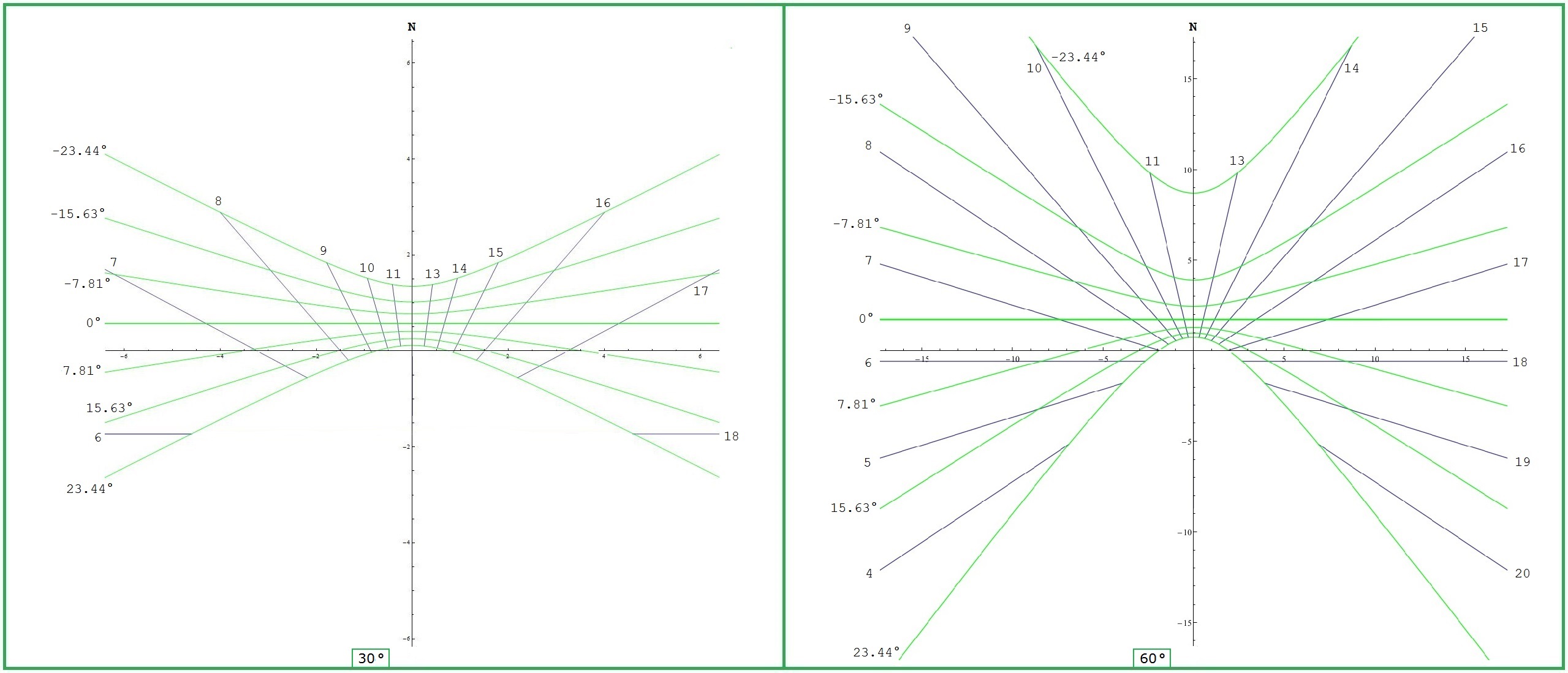
`60°`	`≥` `-23,44°`	`—`	`τ` `∈` `(arccos(1,732·tan` `δ), 360°-` `arccos(1,732·tan` `δ))`	`(41,33°,` `318,67°) ≈` `(02:45,` `21:15)`	`(138,67°,` `221,33°) ≈` `(09:55,` `14:45)`	`δ` `>` `arctan(0,577·cos` `τ)`	`√3 ≈ 1,732 1/√3 ≈ 0,577` siehe Bild 5
`51°34'`	`≥` `-23,44°`	`—`	`τ` `∈` `(arccos(1,260·tan` `δ), 360°-` `arccos(1,260·tan` `δ))`	`(56,88°,` `303,12°) ≈` `(03:48,` `20:12)`	`(123,12°,` `236,88°) ≈` `(08:12,` `15:48)`	`δ` `>` `arctan(0,794·cos` `τ)` `δ` `≤` `23,44° wurde nicht eingehalten.`	Hoheward siehe Bild 3
`50°`	`≥` `-23,44°`	`—`	`τ` `∈` `(arccos(1,192·tan` `δ), 360°-` `arccos(1,192·tan` `δ))`	`(58,89°,` `301,11°) ≈` `(03:56,` `20:04)`	`(121,11°,` `238,89°) ≈` `(08:04,` `15:56)`	`δ` `>` `arctan(0,839·cos` `τ)`	siehe Bild 4
`30°`	`≥` `-23,44°`	`—`	`τ` `∈` `(arccos(0,577·tan` `δ), 360°-` `arccos(0,577·tan` `δ))`	`(75,50°,` `284,50°) ≈` `(05:02,` `18:58)`	`(104,50°,` `255,50°) ≈` `(06:58,` `17:02)`	`δ` `>` `arctan(1,732·cos` `τ)`	`1/√3 ≈ 0,577 √3 ≈ 1,732` siehe Bild 5
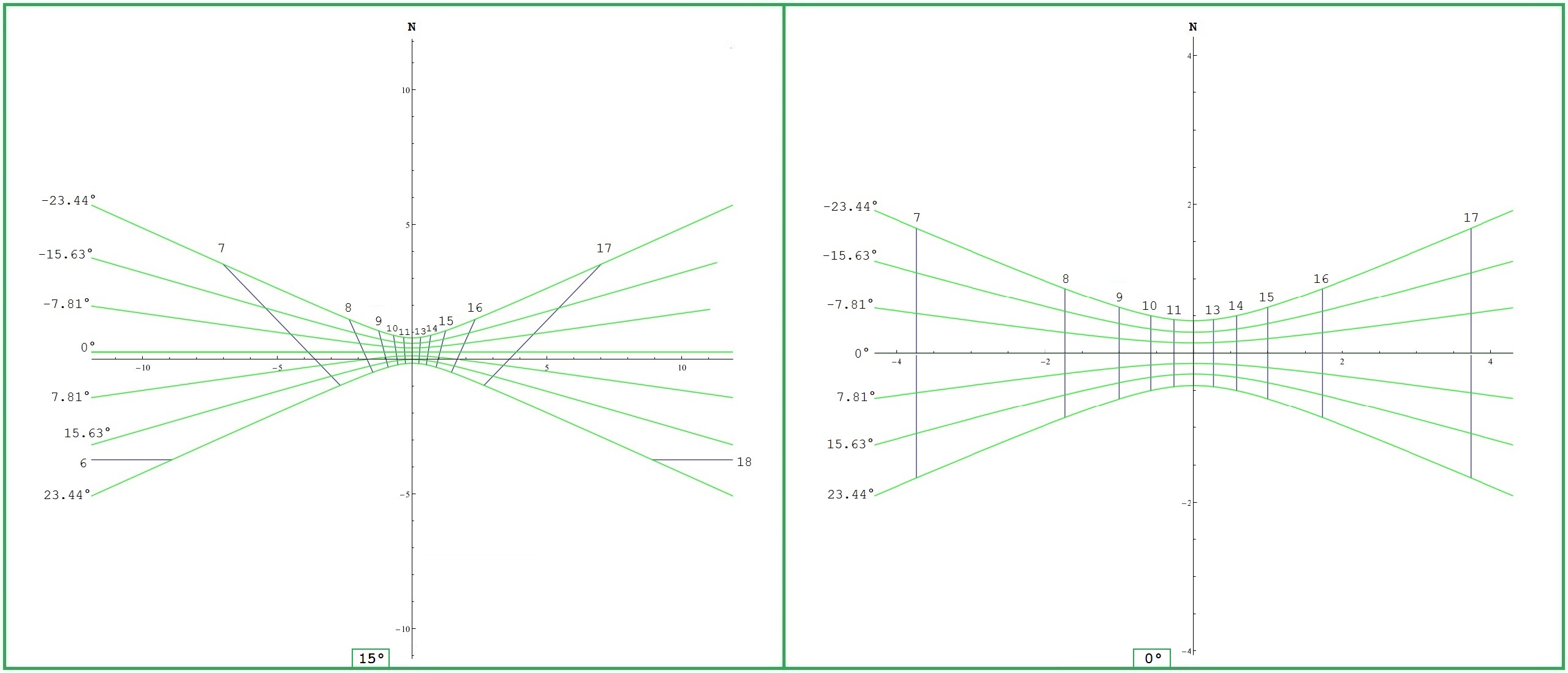
`15°`	`≥` `-23,44°`	`—`	`τ` `∈` `(arccos(0,268·tan` `δ), 360°-` `arccos(0,268·tan` `δ))`	`(83,33°,` `276,67°) ≈` `(05:33,` `18:27)`	`(96,67°,` `263,33°) ≈` `(06:27,` `17:33)`	`δ` `>` `arctan(3,732·cos` `τ)`	`2` `-` `√3 ≈ 0,268 2` `+` `√3 ≈ 3,732` siehe Bild 7
`0°`	`≥` `-23,44°`	`—`	`τ` `∈` `(90°,` `270°)` `=` `(06:00,` `18:00)`	`(90°,` `270°) =` `(06:00,` `18:00)`	`(90°,` `270°) =` `(06:00,` `18:00)`	`Ausnahme: τ` `∈` `D₁: δ` `≥` `-23,44°`	Äquator siehe Bild 7
`-50°`	`≥` `-23,44°`	`—`	`τ` `∈` `(arccos(-1,192·tan` `δ), 360°-` `arccos(-1,192·tan` `δ))`	`(58,89°,` `301,11°) ≈` `(03:56,` `20:04)`	`(121,11°,` `238,89°) ≈` `(08:04,` `15:56)`	`Ausnahmen: Rd.pkt.` `D₂:` `δ` `∈` `[-23,44°,` `23,44°) τ` `∈` `D₁∖D₂: δ∈[-23,44°,arctan(-0,839·cos` `τ))`	siehe Bild 4

Tabelle 2 Numerische Werte sind gerundet.

Die folgenden Graphiken setzen Bild 4 fort und beziehen sich auf Tabelle 2. Sie haben verschiedene Maßstäbe. Die Achsenbeschriftungen geben Anhaltspunkte für die Schattenlängen.

Wegen der Symmetrie zwischen Nord- und Südhalbkugel (siehe Bild 4 und (V) - (X)) wurde bei den Bildern 5 - 7 nur die Nordhalbkugel berücksichtigt.

Die ganzen Zahlen an den Graphen sind Uhrzeiten, die Angaben in Grad sind Deklinationen.

Die jeweils 7 grünen δ-Linien in den Bildern 4 - 7 sind im Intervall [-23,44°, 23,44°] äquidistant eingeteilt, außer in Bild 6. Bei einer realen Konstruktion wird man natürlich mehr Deklinationslinien zeichnen. Für die Umrechnung der Deklinationen in Daten benutzt man eine → Tabelle.

30 60 Grad

Bild 5 Gemäßigte Zone: φ = 30° und φ = 60°;
alle Deklinationen kommen vor.

75 90 Grad

Bild 6 Nordpolarregion: φ = 75° und φ = 90°;
alle Tageszeitlinien sind unendlich lang.

15 0 Grad

Bild 7 Tropen: φ = 15° und φ = 0°,
alle Deklinationen kommen vor; am Äquator sind alle Tageszeitlinien endlich.

Wie schon in meinen vorangegangenen Blog-Beiträgen soll auch hier auf den Unterschied zwischen der durch die Sonnenuhr angezeigten Zeit und der bürgerlichen Zeit hingewiesen werden.

Die Ablesung der Gnomon-Sonnenuhr führt auf die wahre lokale Sonnenzeit. Zum Vergleich mit der bürgerlichen Zeit (also mit der Armbanduhr) müssen noch folgende Anpassungen vorgenommen werden:

Zeitgleichung zur Ermittlung der mittleren lokalen Sonnenzeit.

Längengradkorrektur (also muss die geographische Länge genau ermittelt werden; außerdem diejenige geographische Länge, die der bürgerlichen Zeit zu Grunde liegt, z.B. in Deutschland im Winter 15° Ost für MEZ ; die Differenz macht in Ost-West-Richtung 4 min pro Längengrad aus).

Ggfs. eine Korrektur von einer Stunde, falls die Sommerzeit gilt.

Beispiel: Unsere Gnomon-Sonnenuhr (Höhe Gnomon 1 m) möge im Westen Deutschlands bei 51,5° Nord und 6,5° Ost stehen. An einem sonnigen Tag in der zweiten Jahreshälfte lesen wir die Uhrzeit 09:30 und die Deklination +1°20' ab. (Der Vollständigkeit halber: Der Schatten ist dann 1,678 m lang, und die Sonne steht im Südosten bei 134,888°.) Das entspricht dem Datum 20. September mit Zeitgleichung +7 min . Die Sonne geht also 7 Minuten gegenüber der mittleren Zeit vor. Damit erhalten wir:

09:30 Uhr wahre lokale Sonnenzeit
= 09:23 Uhr mittlere lokale Sonnenzeit
= 09:57 Uhr MEZ (denn MEZ bezieht sich auf 15° Ost; die Differenz von 8,5° entspricht 34 min)
= 10:57 Uhr Sommerzeit, also aktuelle bürgerliche Zeit

Quellen

[1] Sonnenuhren auf Astronomie.de

[2] Bauer: Geschichtliche Entwicklung der Sonnenuhren in verschiedenen Kulturen. In: Verm.-Ing. 1998, S. 356-358

[3] Minow: Schattenmessung mit dem Gnomon. In: ZfV. Zeitschrift für Geodäsie, Geoinformation und Landmanagement. 130, Heft 4, 2005, S. 248-252

[4] Sonnentaler: Sonnenuhr

Kategorie: Geomathematik Kommentare sind willkommen.

Stand 2021-12-19

Inhalt Blog | voriger Eintrag | nächster Eintrag

Manfred Börgens | Zur Leitseite