Ein mathematischer Kurzkrimi

          Die Lösung steht im unteren Teil der Seite.

Hier finden sie mich nie, dachte Bert. "Sie" waren seine Freunde zu Hause in Stockholm, auf deren Hilfe er dringend angewiesen war. Seit seiner Entführung war er gefühlt um die halbe Welt gefahren und geflogen worden. Am Vorabend hatte er erkennen können, dass er sich auf einem Boot befand, das in einiger Entfernung vor einer kleinen Insel ankerte. Seine Entführer sprachen kein Schwedisch und verständigten sich mit ihm in gebrochenem Englisch. Sie hatten ihn sehr früh geweckt; noch vor Sonnenaufgang teilten sie ihm mit, wie sie sich vorstellten, an das Lösegeld zu kommen. Er sollte seinen Anwalt anrufen, ihm die Lösegeldforderung übermitteln und ihm einen weiteren Anruf am Abend ankündigen, bei dem Ort und Zeit der Übergabe mitgeteilt würden.

Die Entführer hatten offenbar keine Bedenken, dass er bei den Telefonaten Hinweise auf seinen Aufenthaltsort geben könnte. Bert hatte ja selbst keine Idee, wo er war. Seine Uhr und sein Smartphone hatte man ihm abgenommen. Eine Hoffnung, wie er von seinen Freunden gefunden werden könnte, war bereits zerstoben: Er hatte daran gedacht, möglichst lange zu telefonieren, so dass das Boot geortet werden konnte. Seine Entführer hatten ihm klargemacht, dass dies zwecklos war. Die Telefonate gingen nicht direkt nach Stockholm, sondern an ein Gerät eines Komplizen in einer anderen Stadt, das in seinem Köfferchen lag und die Gespräche unmittelbar an den Anwalt weiterleiteten. Der Komplize (der wohl auch keine Fremdsprachen konnte) würde während dieser technischen Trickschaltung mit dem Köfferchen in einem Park sitzen und gleich nach jeder dieser Kommunikationen alles abschalten und nach Hause gehen.

Bert war Mathematiker. Er dachte nach. Es wurde schon dämmrig, der Himmel war klar und die See ruhig. Die Entführer hatten ihm Zeit eingeräumt, sich auf das Telefonat vorzubereiten und seinem Anwalt seine missliche Lage klarzumachen. Dieser sollte seine Freunde (auch Mathematiker) kontaktieren, damit sie das Lösegeld beschafften. Insgeheim hoffte Bert natürlich, dass ihm noch irgendein Hinweis einfiele, der zu seiner Befreiung führen würde. Die Entführer schienen ihm offenbar freie Hand zu lassen, wann er die Anrufe machen wollte.

Berts Nachdenken war erfolgreich.

In der nächsten Nacht überraschten drei Männer einer Spezialeinheit die Entführer im Schlaf und befreiten Bert.

Wie haben seine Freunde ihn gefunden?

Lösung

Dieses Problem geht zurück auf einen Riddler Express vom 7. Juni 2019. Die wöchentliche Riddler-Kolumne auf der Website  FiveThirtyEight  gehört zum Besten, was an mathematischen Rätseln im Internet zu finden ist. Hier wurde nur der Kontext des Problems neu formuliert. Die Riddler-Lösung war einleuchtend, wurde aber nur qualitativ beschrieben und nicht mathematisch ausgeführt. Das soll hier nachgeholt werden.

Auf welche gute Idee war Bert gekommen, die zu seiner Befreiung führte?

Bert wartete den richtigen Zeitpunkt ab, um dem Anwalt mitzuteilen, dass gerade die Sonne aufging.

"... so, die Lösegeldforderung kennen Sie jetzt. Und nun passen Sie gut auf, hier kommt eine wichtige Information für meine Freunde: ... Moment noch ... genau jetzt sehe ich die Sonne aufgehen, sie steht zur Hälfte über dem Horizont ... und ganz wichtig: Ich rufe Sie heute abend wieder an."

→    Falls Sie die Lösung vorher noch nicht gefunden hatten und nun bei Ihnen ein "Ach ja, na klar!"-Gedanke ausgelöst wurde, dann lesen Sie nicht weiter und lösen jetzt das Problem.

Bert wusste, dass seine Mathematiker-Freunde in Stockholm aus seinem morgendlichen Anruf noch nicht auf seine Position schließen konnten. Bild 1 zeigt, warum das so ist. Gezeigt wird ein Tag im Sommerhalbjahr; ein Teil der Nordpolarregion liegt rundum im Sonnenschein.  δ  ist die Deklination der Sonne, die für jeden Tag des Jahres aus einer  → Tabelle ablesbar ist. Somit befindet sich Bert auf dem halben Großkreis um die Erde (schräger blauer Durchmesser in Bild 1), auf dem gerade die Sonne aufgeht.


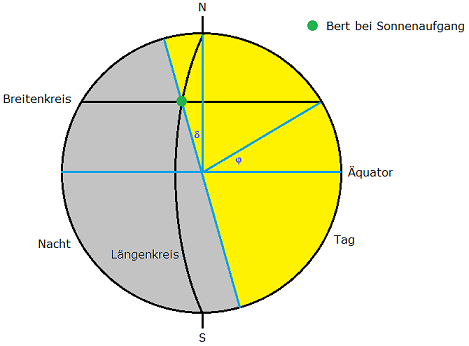
Bild 1

Bert setzte alles daran, sein abendliches Telefonat mit dem Anwalt bei Sonnenuntergang führen zu können. Wir wissen, dass ihm das gelungen ist, denn er wurde befreit. Es wird für den Anwalt und für Berts Freunde ein Leichtes gewesen sein, die genauen Zeitpunkte von Berts Mitteilungen festzuhalten. Seine Freunde (zur Erinnerung: das sind Mathematiker!) hatten also folgende Informationen:

-  Uhrzeit in Stockholm beim Sonnenaufgang an Berts Position
-  Uhrzeit in Stockholm beim Sonnenuntergang an Berts Position
-  Deklination  δ ,  die sich aus dem Datum ergibt

→    An dieser Stelle gibt es noch einmal die Gelegenheit, nicht weiterzulesen und sich an die Arbeit zu machen.


Achtung:  Ortszeit

Möglichst genaue Zeitangaben sind wichtig für die Lösung des Problems. Da es um den Sonnenstand geht, und weil Bert keine Uhr hat, ist die Ortszeit an Berts Position von Bedeutung. Diese ist normiert durch die Festlegung, dass bei Sonnenhöchststand ("Mittag") es genau  12:00:00 Uhr  ist.

Welche Uhrzeit verwenden der Anwalt und Berts Freunde in Stockholm? Dort gilt im Juni die  Mitteleuropäische Sommerzeit  UTC+2 ,  die auch in Deutschland gültig ist. Dies ist die über das Jahr gemittelte Ortszeit des  30. östlichen Meridians, der am westlichen Rand von St. Petersburg und von Kiew und durch Alexandria in Ägypten verläuft. Warum wird die Ortszeit gemittelt? Wenn man seine Uhr nach der Ortszeit, also nach dem Sonnenstand einstellen möchte, stellt man fest, dass im Jahresverlauf die Tage nicht gleich lang sind, sondern sich ihre Dauer um einige Sekunden unterscheidet. Das reicht immerhin dazu aus, dass die Aufsummierung dieser Über- oder Unterschüsse zu Unterschieden zwischen einer Sonnenuhr und unserer Armbanduhr im Minutenbereich führt (im Maximum ca. 16  Minuten). Die so entstehende Differenz nennt man Zeitgleichung; Berts Freunde müssen sie in ihre Zeitrechnungen einbeziehen.


Die leichte Aufgabe: Längengrad

Will man für zwei verschiedene Positionen auf der Erde den Abstand der Längengrade feststellen, bietet sich ein Uhrenvergleich an. Was können die Freunde in Stockholm über Berts Ortszeit wissen? Beim ersten Anruf noch gar nichts, denn sie kennen ja die Aufgangszeit (Ortszeit) der Sonne an Berts Position nicht. Aber durch den Anruf bei Sonnenuntergang wissen Sie, wie lange bei Bert die Sonne am Himmel stand. Beide Zeiten halten Sie in ihrer eigenen Zeit  UTC+2  fest; genau in der Mitte liegt Berts Mittagszeit. Für diesen Zeitpunkt kennen die Freunde also sowohl Berts Ortszeit  12:00:00  als auch die Zeit nach  UTC+2 .  Pro Stunde rückt die Sonne um  15°  Länge von Ost nach West weiter, so dass es naheliegt, Berts Längengrad  λ  mittels  Zeitdifferenz in Stunden × 15  zu finden. Aber Vorsicht: Der Referenzmeridian  30° Ost  für  UTC+2  ist nur im jährlichen Mittel korrekt, wie im vorigen Abschnitt erläutert wurde. Also muss noch eine Korrektur für die Zeitgleichung vorgenommen werden.

Zeitgleichungs-Korrektur: Im Beispiel weiter unten beträgt die Zeitgleichung  -50  Sekunden. Das bedeutet, dass die Sonnenuhr um  50  Sekunden gegenüber der Armbanduhr nachgeht. Bei der Zeitdifferenz, die Berts Freunde zur Berechnung von  λ  zugrunde legen, müssen diese  50  Sekunden subtrahiert werden.


Achtung:  Refraktion

Wir kommen gleich zur Berechnung von Berts Breitengrad  φ .  Dabei spielt die Ortszeit des Sonnenaufgangs an Berts Position die entscheidende Rolle (man kann statt dessen natürlich auch den Untergang nehmen). Im mathematischen Modell, das für die Berechnung von  φ  in Abhängigkeit von dieser Ortszeit herangezogen wird, wird die Lufthülle der Erde (zunächst) nicht berücksichtigt. Berts Freunde wissen, dass Bert die Sonne deutlich früher sehen kann, als wenn es keine Lufthülle gäbe. Die Ablenkung der Lichtstrahlen durch die Atmosphäre nennt man Refraktion. Benutzt man also eine der üblichen Formeln zur Berechnung von  φ ,  so ist zu der beobachteten Aufgangszeit ein der Refraktion entsprechender Korrekturterm zu addieren.


Die schwere Aufgabe: Breitengrad

Berts Ortszeit bei Sonnenaufgang ist Berts Freunden aus der Längengradberechnung bereits bekannt, da sie die Zeitdauer zwischen Aufgang und Untergang der Sonne kennen und diese symmetrisch zu  12:00:00 Uhr  liegen.

Man muss nicht lange suchen, ehe man eine Formel für den Zeitpunkt  τ  des Sonnenaufgangs findet, siehe z.B. (41) in der Formelsammlung auf dieser Website. Hier ist sie:

(1)   cos τ = tan φ · tan δ

τ  gibt die Zeit nach Mitternacht in Grad an (24 h = 360°), φ  ist der gesuchte Breitengrad und  δ  die Deklination der Sonne (siehe Bild 1). In anderen Quellen (siehe z.B.  → hier) ist oft die Zeit um  180° verschoben (also Nullpunkt am Mittag statt um Mitternacht), so dass dort  -cos  statt  cos  genommen wird.

Damit erhalten wir die folgende Lösung:

(2)   φ = arctan(cos τ · cot δ)

Wieso handelt es sich um eine "schwere" Aufgabe? Nun, vielleicht möchte man die Gleichung (1) nicht einfach irgendwo ablesen, sondern selbst herleiten. Und dafür benötigt man einige Elemente der Geomathematik. Um den Fluss dieser Lösung nicht zu unterbrechen, wird die Herleitung von (1) ausgelagert:  →  Beweis.

Die Korrektur von Berts Ortszeit bei Sonnenaufgang wird für seine Freunde nicht ganz einfach sein. Die Refraktion hängt u.a. von den Wetterverhältnissen ab. Außerdem müssen sie wissen, wie hoch Bert über der Wasseroberfläche steht, wenn er den Sonnenaufgang beobachtet  -  denn die angegebene Formel für  φ  geht von einer Höhe von  0  aus, d.h. es wird der Zeitpunkt genommen, an dem die Strahlen einer theoretisch als punktförmig angenommenen Sonne den Fußpunkt des Betrachters erreichen. Berts Freunde sind natürlich in der Lage, aus Berts Augenhöhe die entsprechende Zeitdifferenz zu berechnen (siehe z.B. (5.6) in Blog # 2 Erdradius). Beide Korrekturen (der Anteil der Refraktion ist mit ca. 2  Minuten der deutlich dominante) gehen in dieselbe Richtung: Der Zeitpunkt  τ ,  der in (2) eingesetzt werden muss, liegt später als der von Bert mitgeteilte Zeitpunkt. Wir vertrauen der Expertise der Freunde, für die Refraktion eine möglichst gute Schätzung abzugeben. Wie stark sie sich höchstens irren sollten, um Bert nicht zu verfehlen, wird weiter unten noch diskutiert.


Beispiel

14. Juni 10:16:54 UTC+2    1. Anruf    Sonnenaufgang bei Bert
15. Juni 02:03:06 UTC+2    2. Anruf    Sonnenuntergang bei Bert

   →  14. Juni 18:10:00 UTC+2    Mittag bei Bert
                             12:00:00    Mittag Ortszeit Bert
                             Zeitgleichung = -50''

   →            6^h 09' 10''  UTC+2 + Zeitgleichung - Mittag Ortszeit Bert
   →            92°17' 30''    Differenz (zwischen 30° Ost und Berts Längengrad)

                             UTC+2 = 30° Ost

   →        λ = 62° 17' 30'' W    Berts Längengrad

14. Juni 04:06:54 Ortszeit Bert    Sonnenaufgang bei Bert
         04:09:14 Ortszeit Bert    Sonnenaufgang bei Bert mit Korrektur
                                                                     Korrektur Refraktion / Augenhöhe
              →  τ = 62° 18' 30'

14. Juni      →  δ = 23° 15'

   →        φ = 47° 14' 46'' N    Berts Breitengrad


Achtung:  Messungenauigkeit

Wir wollen versuchen, eine Toleranz für die von Berts Freunden berechnete Position anzugeben. Bert befindet sich im Meer, in der Nähe einer kleinen Insel. Die Suche ist also viel einfacher als an Land. Abweichungen von bis zu  5 km ,  evtl. auch  10 km  bei der Positionsangabe sollten kein großes Hindernis beim Auffinden des Bootes sein.

(1) macht eine Reihe von vereinfachenden Annahmen, z.B. die Kugelform der Erde, die aber die Ergebnisse nur wenig verfälschen. Außerdem wurde im Beispiel gerundet, aber auch dies wird die Berechnung von Berts Position nicht erschweren.

Etwas genauer sollte man sich den Einfluss der unterschiedlichen Tageslängen anschauen, die die Ursache der Zeitgleichung sind. In unserem Beispiel geht es um Mitte Juni; der wahre Sonnentag ist dann ca. 24  Stunden und  12  Sekunden lang. Dies beeinflusst die Berechnung von  λ :  der beobachtete Sonnenaufgang liegt einige Sekunden mehr vom Mittag entfernt als erwartet. Dies macht etwa  1 km  Differenz in West-Ost-Richtung aus.

Wie genau kann Bert angeben, wann er die obere Hälfte der Sonne sieht? Das ist nicht ganz einfach, und wir wollen eine Beispielrechnung durchführen, in der Bert das Signal bei Sonnenaufgang  10  Sekunden zu früh nach Stockholm schickt.

Differenz  Δ :
Δ(λ) ≈ 1'15'' ≈ 1,6 km
Δ(φ) ≈ 1'11'' ≈ 2,2 km

Fehler in dieser Größenordnung wären noch vertretbar. Wenn man aber ein wenig mit anderen Eingabewerten für Sonnenauf- und -untergang und für  δ  experimentiert, fällt sofort auf, dass eine ausreichende Genauigkeit zur Zeit der Tag- und Nachtgleichen nur schwer erreichbar ist. Das ist auch leicht einzusehen: Um diese Zeiten dauert der lichte Tag fast überall etwa  12  Stunden, was die Bestimmung des Breitengrads sehr erschwert. Wir demonstrieren das an einem Beispiel, das wieder von einem um  10  Sekunden zu frühen Sonnenaufgang ausgeht  -  τ  verschiebt sich dadurch um  5  Sekunden:

δ = 3°     τ = 05:50:49  bzw. 05:50:44
Differenz  Δ :
Δ(λ) ≈ 1'15'' ≈ 1,8 km
Δ(φ) ≈ 15' ≈ 27,8 km

Die Abweichung im Breitengrad erschwert die Auffindung von Bert erheblich. Der Effekt der Deklination  δ  wird durch Bild 2 deutlich:


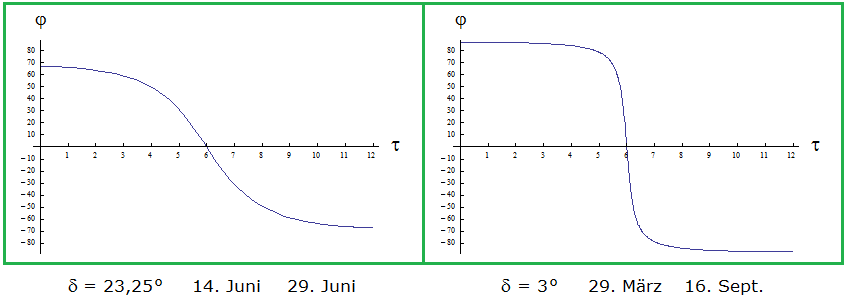
Bild 2



Dieses Problem wird im Blogbeitrag # 23 erneut aufgegriffen und etwas erweitert.



Kategorie: Geomathematik

Publiziert 2022-09-20          Stand 2020-06-15

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem