Nachbarn Diese Seite wurde 2021-04-19 ajouriert. |
|
 English version English version |
Die Lösung steht im unteren Teil der Seite.
|
|
|
In einem Dorf seien die Abstände der Häuser paarweise verschieden.
Wenn es n Häuser gibt, gibt es n(n-1)/2 unterschiedliche Abstände.
Der Geselligkeitsverein des Dorfes fordert alle Einwohner auf, im Laufe des kommenden Mittwochs ihr nächstes Nachbarhaus zu besuchen.
Die Einwohner sollen sich vorher über die Besuchstermine absprechen, denn dies gebietet die Höflichkeit, aber vor allem, weil es vorkommen kann, dass sich die Bewohner zweier Häuser gegenseitig besuchen. Außerdem wollen wir unterstellen, dass an diesem Mittwoch keine weiteren Besuche stattfinden. — Das Problem, das wir im Folgenden vorstellen wollen, hängt nicht davon ab, wieviele Menschen in den einzelnen Häusern leben, so dass wir der Einfachheit halber annehmen können, dass es genau einen Bewohner pro Haus gibt.
|
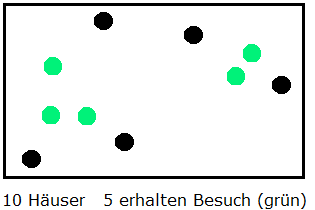 |
|
Schon Beispiele mit wenigen Häusern zeigen, dass manche Dorfbewohner Besuch bekommen, andere aber nicht.
Wie hängt das von der Anzahl der Häuser ab?
Diese Frage soll etwas präziser formuliert werden. Man kann z.B. mit einem konkreten Problem beginnen: Das Dorf möge 7 Häuser haben; wieviele Häuser können besucht werden? Hier wird also nach möglichen Anordnungen der Häuser gefragt. Kommt für die Anzahl m der besuchten Häuser jedes m ∈ {1, ..., 7} in Frage?
Zum allgemeinen Problem: Kommt für die Anzahl m der besuchten Häuser jedes m ∈ {1, ..., n} in Frage? Eine vollständige Lösung wird hier nicht erwartet. Einsteigen kann man mit der Frage, ob es Dorfgrößen n gibt, bei denen nicht alle Häuser besucht werden können. – Damit man nicht endlose Anordnungen der Häuser ausprobieren muss, empfiehlt sich die folgende Systematik: Man geht von den kleinen m zu den großen; für jedes konkrete m überlegt man sich, wie groß n maximal werden kann. - Mit diesem Vorgehen kommt man sehr weit, denn man kann zeigen: Ist die Konstellation (n,m) erlaubt, dann gilt dies auch für alle (n0,m) mit n0 < n und alle (n,m0) mit m0 > m , jeweils mit maximal einer Ausnahme. – Wenn man nur bis m = 4 geht, erhält man schon eine Lösung bis n = 18 (m = 7 → n = 30).
Lösung
Bei diesem Problem begegnet uns eine Besonderheit, die auf diesen Seiten üblicherweise nicht vorkommt: Es handelt sich um ein nicht vollständig gelöstes Problem.
Durch Ausprobieren erhält man ziemlich leicht Lösungen für n Nachbarn, von denen m besucht werden. Die Beispielfrage in der Aufgabenstellung für n = 7 ergibt folgende Lösungen:

Bild 1 n = 7 grün : besuchte Häuser
Die Anordnungen in Bild 1 stellen natürlich nur mögliche Positionen der Häuser dar; auch andere Positionen lassen sich finden. Dargestellt wurde m ∈ {2, 3, 4, 5, 6}. Für m = 7 finden wir keine Anordnung der Häuser. Als "erlaubte" Paare (n,m) wollen wir solche bezeichnen, für die wir eine passende Anordnung gefunden haben. Das führt zu einem ersten Ergebnis für erlaubte (n,m) :
Das lässt sich leicht beweisen. m = 1 scheidet aus, weil sich die Nachbarn in den beiden Häusern mit dem kleinsten Abstand gegenseitig besuchen. – Wie steht es mit m = n ? Offenbar ist das für gerade n möglich, da es dann n/2 Paare nah zusammen wohnender Nachbarn geben kann, die sich jeweils gegenseitig besuchen. – Sei nun n ungerade. Wir gehen induktiv vor. Für n = 3 ist klar, dass ein Nachbar keinen Besuch bekommt. Für größere n besuchen sich die beiden nächsten Nachbarn A und B gegenseitig; für die restlichen n - 2 gibt es zwei Möglichkeiten:
Erster Fall: Von den n - 2 Nachbarn besucht (mindestens) einer A oder B ; dann bleiben nur noch (höchstens) n - 3 mögliche Besucher der n - 2 Häuser übrig; also bleibt (mindestens) ein Haus unbesucht.
Zweiter Fall: Von den n - 2 Nachbarn besucht niemand A oder B ; dann gibt es n - 2 mögliche Besucher der n - 2 Häuser; dafür greift die Induktionsvoraussetzung, nach der (mindestens) ein Haus unbesucht bleibt.
Zur Einstimmung auf das allgemeine Problem werden in Bild 2 mögliche Anordnungen der Häuser für m = n - 1 (n ungerade) und m = n (n gerade) dargestellt:

Bild 2 m = n - 1 m = n schwarz : unbesuchtes Haus
⬛ m = 2 und m = 3
Durch Ausprobieren stellt sich die Vermutung ein, dass es für jedes m eine Obergrenze für n gibt. In Bild 3 sieht man mögliche Anordnungen der Häuser für (n,m)=(9,2) und (n,m)=(12,3).
Leserinnen und Leser können versuchen, für m = 2 bzw. m = 3 größere n als 9 bzw. 12 zu finden.
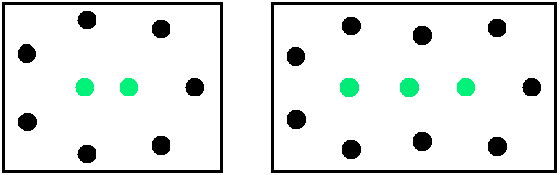
Bild 3 (n,m)=(9,2) (n,m)=(12,3) grün : besuchte Häuser
Wie kommen die Anordnungen der Häuser in Bild 3 zustande? Es ist naheliegend (aber nicht zwingend), zunächst eine geometrische Anordung mit gleichseitigen Dreiecken wie in Bild 3a zu wählen. Alle dort eingezeichneten Verbindungsstrecken haben die gleiche Länge. Dann werden alle Punkte minimal verschoben, damit alle Abstände verschieden sind; diese Verschiebungen sollen außerdem gewährleisten, dass für jeden schwarzen Punkt (unbesuchte Häuser) ein grüner Punkt der nächstliegende ist. Das ist leicht zu bewerkstelligen, siehe Bild 3.
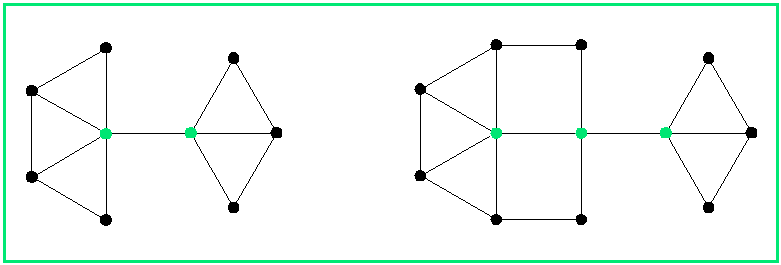
Bild 3a
⬛ m ≥ 4
Wir wollen nun annehmen, dass wir für m = 2 und m = 3 das jeweils maximale n = 9 und n = 12 gefunden haben. Nun könnte man so fortfahren für m = 4, 5 usw. Aber das ist nicht nötig und nicht günstig, da man die beiden Konstellationen aus Bild 3 vervielfältigen und kombinieren kann. Um für jedes m ein möglichst großes n zu erzielen, kann man für gerade m mehrere "Inseln" vom Typ (9,2) aufstellen. Für ungerade m nimmt man eine einzige "Insel" vom Typ (12,3) hinzu. In Bild 4 wird das für (n,m)=(57,13) gezeigt:
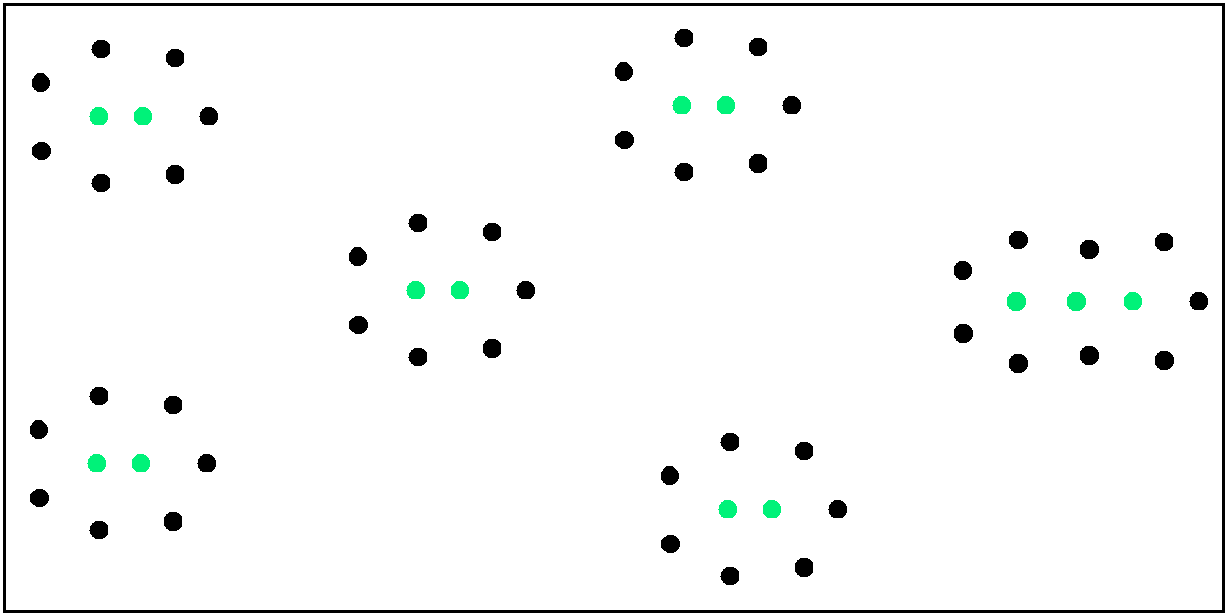
Bild 4
Das bedeutet für i Inseln:
m = 2i → n = 9i
m = 2i+1 → n = 9i+3
Die entsprechenden "Ankerfelder" sind in der Matrix in Bild 5 grün markiert. Sie stehen für (n,m) mit dem (soweit bekannt) größten n , das für m in Frage kommt. Die anderen Kreuze in der Matrix stehen für (n,m), deren Möglichkeit schon in Bild 1 und Bild 2 gezeigt wurde. Die orangenen Felder stehen für m = n ungerade; es wurde oben gezeigt, dass dazu keine Anordnung existiert.
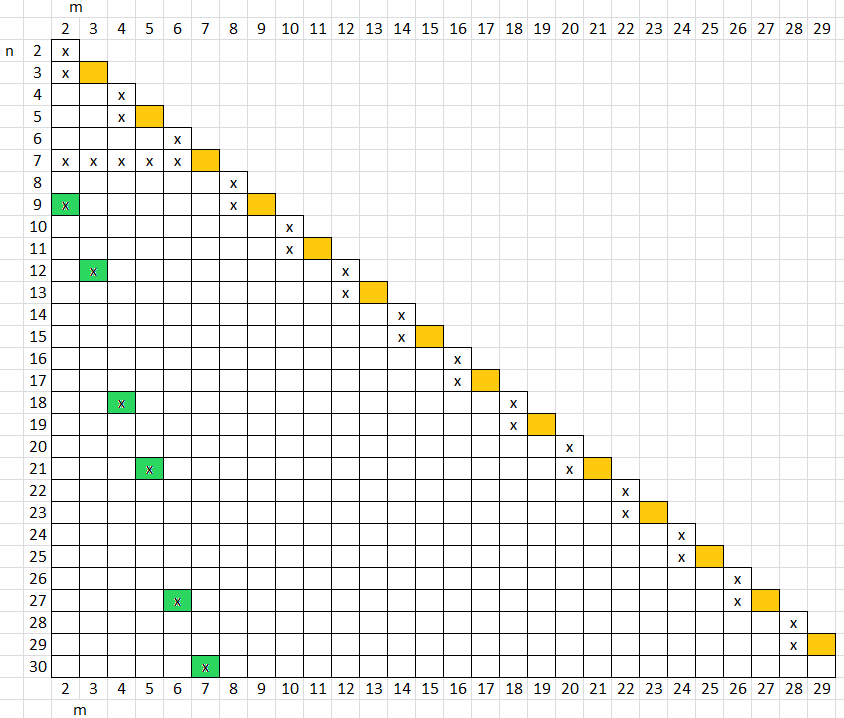
Bild 5
Nun soll die Matrix in Bild 5 "gefüllt" werden. Wir werden zeigen, dass für alle m die m-te Spalte oberhalb des grünen Ankerfelds bis (m,m) für gerade m und bis (m+1,m) für ungerade m "aufgefüllt" werden kann, d.h. dass dort erlaubte Anordnungen existieren. Dies ist aber leicht zu beweisen: In der linken Skizze von Bild 3 lassen sich nach und nach alle schwarzen Punkte entfernen; in der rechten Skizze gilt das auch, mit Ausnahme eines schwarzen Punktes am linken Rand (man beachte, dass der mittlere grüne Punkt seinem rechten Nachbarn näher liegt als seinem linken); die grünen Punkte und ihre Abstände bleiben erhalten – mit diesem Verfahren, dass sukzessive für alle "Inseln" durchgeführt wird, bleibt m gleich, während n schrittweise reduziert wird. Die Wegnahme der schwarzen Punkte lässt sich auch gut anhand von Bild 4 nachvollziehen. Das Ergebnis sieht man in Bild 6.
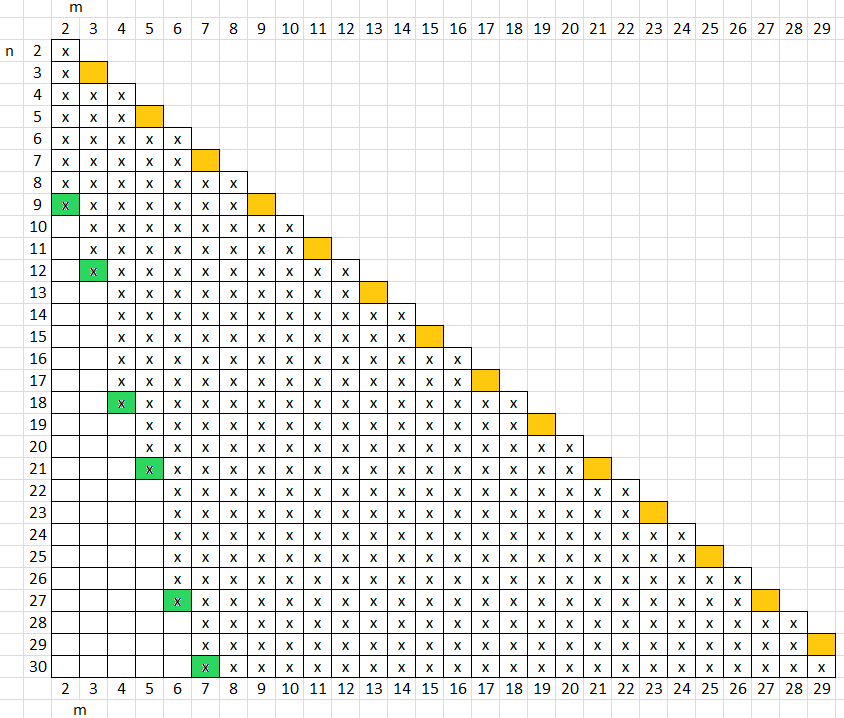
Bild 6
x: erlaubte Anordnung
grün: Ankerfeld
orange: keine erlaubte Anordnung
weiß: unbewiesene Vermutung: keine erlaubte Anordnung
Nun wissen wir, wie weit man für jedes m mit n (mindestens) kommen kann. Werden beispielsweise 9 Häuser besucht, so zerlegt man 9 = 2+2+2+3 ; jede 2 steht für eine Anordnung wie links in Bild 3, also für 9 Häuser (besuchte und unbesuchte); der Summand 3 steht für eine Anordnung wie rechts in Bild 3, also für 12 Häuser. Deshalb läuft die Anzahl aller Häuser von 10 bis 39 . Durch das geschilderte Verfahren (mit den Formeln über Bild 5) erhalten wir für jedes m ≥ 2 :
m gerade → nmin = m nmax = 9 m/2
m ungerade → nmin = m + 1 nmax = (9 m - 3)/2
nmax ist das größte n , für das gezeigt werden konnte, dass das Paar (n,m) erlaubt ist. Also ist nmax eine untere Schranke für das "reale" maximale n .
Damit lässt sich eine Folge a(n) der bekannten oberen Schranken für die minimal möglichen m in Abhängigkeit von n aufstellen:
a(2) = a(3) = 2
/ 2j für n = 9j-5 ... 9j
a(n) = j ∈ N
\ 2j+1 für n = 9j+1 ... 9j+3
Alle Leserinnen und Leser dieser Seite sind aufgefordert, weitere erlaubte Anordnungen der Häuser zu finden – oder sogar eine allgemeine Regel aufzustellen.
Abschließend noch ein Beispiel, das nicht von m ausgeht, sondern wie in der Aufgabenstellung von n :
Das Dorf bestehe aus 23 Häusern. Falls die Matrix in Bild 6 bereits optimal sein sollte, erhalten mindestens 6 Häuser Besuch. Mindestens ein Haus erhält keinen Besuch. Von 6 bis 22 besuchten Häusern lässt sich für jede Anzahl ein passendes Dorf darstellen.
Offen ist, ob sich mmin = 6 noch verbessern (d.h. verkleinern) lässt.
A347941 auf OEIS a(n) in der Zahlenfolgen-Datenbank
A261953 auf OEIS Die zu a(n) "inverse" Folge in der Zahlenfolgen-Datenbank
Next Neighbours auf GitHub Eine erweiterte Version dieses Beitrags mit Mathematica-Programmen
Arranging points on plane auf reddit Diskussion der ersten Beweisschritte für dieses Problem
Zum Problem der Nächsten Nachbarn siehe auch Blog # 15 und Problem # 131.
Publiziert 2021-03-26 Stand 2021-11-03
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite
 English version
English version






