Nächste Nachbarn
Wofür steht diese Folge? (2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 10, 11, 11, 11, 12, 12, 12, 12, 12, 12, 13, 13, 13, 14, 14, 14, 14, 14, 14, 15, 15, 15, 16, 16, 16, 16, 16, 16, 17, 17, 17, 18, 18, 18, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 20, 21, 21, 21, 22, 22, 22, 22, 22, 22, 23, ...)
Das Problem der nächsten Nachbarn wurde auf dieser Website ausführlich im Problem 114 behandelt. Eine Ausarbeitung mit Mathematica-Programmen wurde bei → GitHub eingestellt. Eine Diskussion zu den Anfangsschritten dieses Problems wurde bei → reddit geführt.
Die aus dem Problem der nächsten Nachbarn resultierende Zahlenfolge wurde am 1. November 2021 als A347941 in OEIS aufgenommen. Die dazu "inverse" Folge konnte mit A261953 identifiziert werden.
Da es sich um ein nicht vollständig gelöstes Problem handelt, das aufgrund seiner einfachen Formulierung Aufmerksamkeit verdient und das möglicherweise noch weiter ausgelotet werden kann, wird es hier nochmal in Kurzform wiedergegeben:
Wir betrachten eine Menge G von n Punkten in der reellen Zahlenebene mit paarweise verschiedenen Abständen. Ein Punkt A ∈ G ist ein nächster Nachbar, falls es einen Punkt B ∈ G gibt, dessen Abstand zu A kleiner als zu allen anderen Punkten in G ist.
Gesucht ist bei gegebenem n die kleinste mögliche Anzahl b(n) von nächsten Nachbarn. Was ist dazu bisher bekannt?
- Für n ≤ 9 ist das Problem gelöst: b(n) = 2 .
- Für n = 10, 11, 12 ist b(n) ≤ 3 .
- Für n ≥ 13 ist b(n) ≤ 2j für n = 9j-5 ... 9j und b(n) ≤ 2j+1 für n = 9j+1 ... 9j+3, j ≥ 1 .
Damit erhält man eine Folge a(n), die die beste bisher bekannte obere Schranke für b(n) angibt:
- a(2) = a(3) = 2 .
- a(n) = 2j für n = 9j-5 ... 9j, j ≥ 1 .
- a(n) = 2j+1 für n = 9j+1 ... 9j+3, j ≥ 1 .
Dies ist die Folge A347941 in OEIS, die im Kopf dieses Beitrags aufgelistet ist. Zur Veranschaulichung von a(n) sollen die Bilder 1 und 2 dienen.
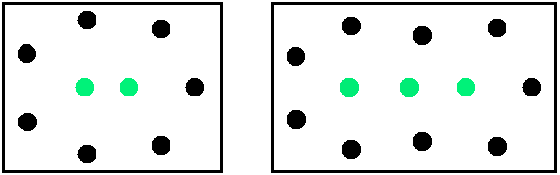
Bild 1 Nächste Nachbarn in Grün.
Links: Für n = 9 (oder weniger) Punkte findet man eine Lösung mit 2 nächsten Nachbarn. Das ist offenbar optimal.
Rechts: Für n = 12 (oder n = 10, 11) Punkte findet man eine Lösung mit 3 nächsten Nachbarn. Geht das auch mit 2 nächsten Nachbarn? Vermutung: Nein.
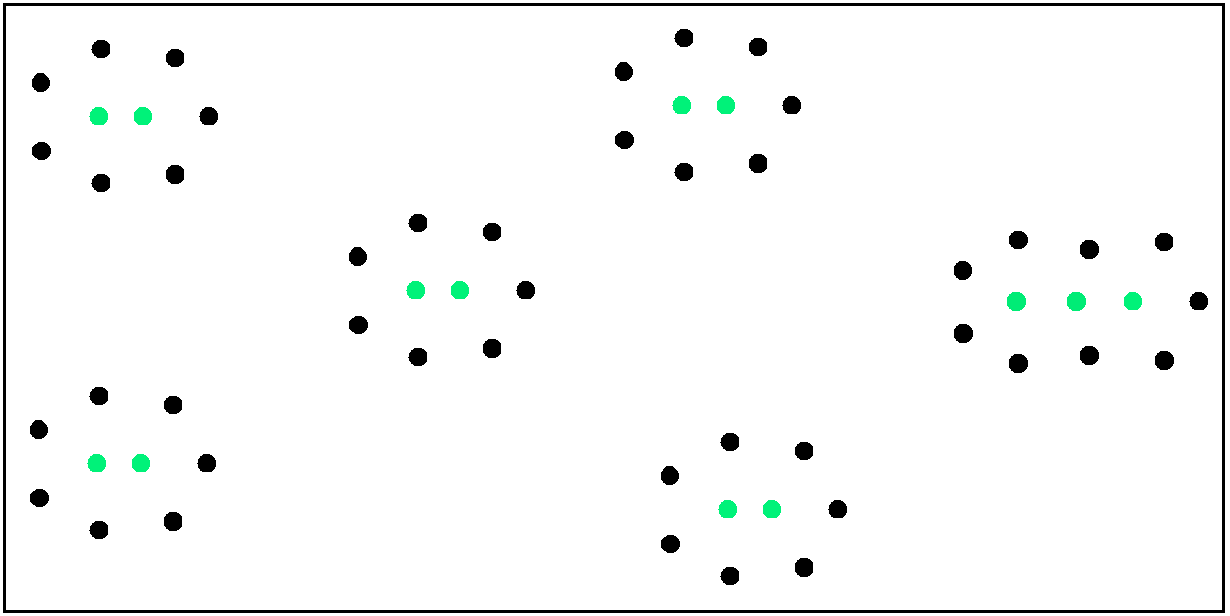
Bild 2 Nächste Nachbarn in Grün. – Für n = 57 Punkte findet man eine Lösung mit 13 nächsten Nachbarn. Geht das auch mit weniger als 13 nächsten Nachbarn? Vermutung: Nein. Diese Vermutung stützt sich auf die Überlegung, dass die Kombination von mehreren Punkte-"Inseln" mit 2 nächsten Nachbarn mit maximal einer Insel mit 3 nächsten Nachbarn optimal ist (Inseln wie in Bild 1 gestaltet, Kombination wie in Bild 2).
Die Bilder 2 und 3 zeigen a(9) = 2, a(12) = 3 und a(57) = 13 . Die komplette Folge wurde weiter oben schon formelmäßig angegeben.
Man kann die Problemstellung umkehren und erhält damit die zu a(n) "inverse" Folge c(m):
Gesucht ist für m nächste Nachbarn die größte mögliche Anzahl d(m) von Punkten in G . Man erhält für m ≥ 2 mit Hilfe von a(n) die Folge c(m) = (9, 12, 18, 21, 27, 30, ...) als beste bisher bekannte untere Schranke für d(m); c(m) findet man in OEIS unter A261953 für m ≥ 2 . – c(5) = 21 bedeutet also, dass man G mit 21 Punkten und 5 nächsten Nachbarn konstruieren kann, aber kein G mit mehr als 21 Punkten und 5 nächsten Nachbarn bekannt ist (Vermutung: Ein solches G gibt es nicht).
Wie können sich Fortschritte zum Problem der nächsten Nachbarn zeigen lassen? Jegliche Kommentare sind willkommen.
- Man zeigt eine positive Teillösung: b(n) = a(n) für konkrete n > 9.
- Man zeigt eine negative Teillösung: Eine oder mehrere der aufgestellten Vermutungen sind falsch – z.B. wird ein G mit 19 Punkten und 4 nächsten Nachbarn präsentiert. Dann müsste a(n) revidiert werden.
Wie lässt sich das Problem der nächsten Nachbarn vollständig lösen? Jegliche Kommentare sind willkommen.
- Man zeigt: a(9) = 2 und a(12) = 3 sind optimal und für alle größeren n ist die "Insel-Technik" aus Bild 2 optimal. Dann ist b(n) = a(n) bewiesen.
- Man gibt b(n) ( ≠ a(n)) vollständig und korrekt an.
Inhalt Blog | voriger Eintrag | nächster Eintrag
Manfred Börgens | Zur Leitseite
MB Matheblog # 15
english version