Nachbarn		English version
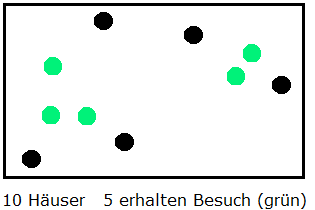
In einem Dorf seien die Abstände der Häuser paarweise verschieden. Wenn es  n  Häuser gibt, gibt es  n(n-1)/2  unterschiedliche Abstände. Der Geselligkeitsverein des Dorfes fordert alle Einwohner auf, im Laufe des kommenden Mittwochs ihr nächstes Nachbarhaus zu besuchen. Die Einwohner sollen sich vorher über die Besuchstermine absprechen, denn dies gebietet die Höflichkeit, aber vor allem, weil es vorkommen kann, dass sich die Bewohner zweier Häuser gegenseitig besuchen. Außerdem wollen wir unterstellen, dass an diesem Mittwoch keine weiteren Besuche stattfinden.  —  Das Problem, das wir im Folgenden vorstellen wollen, hängt nicht davon ab, wieviele Menschen in den einzelnen Häusern leben, so dass wir der Einfachheit halber annehmen können, dass es genau einen Bewohner pro Haus gibt.

Schon Beispiele mit wenigen Häusern zeigen, dass manche Dorfbewohner Besuch bekommen, andere aber nicht.

Wie hängt das von der Anzahl der Häuser ab?

Diese Frage soll etwas präziser formuliert werden. Man kann z.B. mit einem konkreten Problem beginnen: Das Dorf möge  7  Häuser haben; wieviele Häuser können besucht werden? Hier wird also nach möglichen Anordnungen der Häuser gefragt. Kommt für die Anzahl  m  der besuchten Häuser jedes  m ∈ {1, ..., 7}  in Frage?

Zum allgemeinen Problem: Kommt für die Anzahl  m  der besuchten Häuser jedes  m ∈ {1, ..., n}  in Frage? Eine vollständige Lösung wird hier nicht erwartet. Einsteigen kann man mit der Frage, ob es Dorfgrößen  n  gibt, bei denen nicht alle Häuser besucht werden können.  –  Damit man nicht endlose Anordnungen der Häuser ausprobieren muss, empfiehlt sich die folgende Systematik: Man geht von den kleinen  m  zu den großen; für jedes konkrete  m  überlegt man sich, wie groß  n  maximal werden kann. - Mit diesem Vorgehen kommt man sehr weit, denn man kann zeigen: Ist die Konstellation (n,m) erlaubt, dann gilt dies auch für alle (n₀,m) mit  n₀ < n  und alle (n,m₀) mit  m₀ > m , jeweils mit maximal einer Ausnahme.  –  Wenn man nur bis  m = 4  geht, erhält man schon eine Lösung bis  n = 18 (m = 7  →  n = 30).


Lösung

Publiziert 2021-02-25          Stand 2021-04-19

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem