Neighbours		deutsche Version
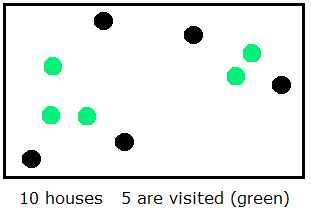
Consider a village where the distances between the houses are pairwise different. If there are  n  houses there will be  n(n-1)/2  different distances. The local Social Club asks all villagers to pay a visit during the following wednesday to their next neighbour. In case that the residents of two houses have to visit each other they are requested to arrange two dates for their visits.  —  We will assume that on this wednesday, no other visits will be paid.  —  The problem presented below does not depend on the number of people living in the houses; we can assume that there is only one inhabitant in each house.

A check of some examples with few houses shows that some villagers will be visited but others will not.

How does this depend on the number  n  of houses?

This question shall be formulated in a more precise manner. To begin with a concrete problem: The village may consist of  7 houses; how many houses can be visited? Here we should consider possible arrangements of the houses. Can the number  m  of visited houses run through all values in  {1, ..., 7}? Give this special problem a try to get a "feeling for the village".

The general problem: Can every  m ∈ {1, ..., n}  stand for the number of visited houses? We do not expect a complete solution. A good start could be the question if there are "village sizes"  n  for which it is impossible that all houses are visited.  —  One should not try endless arrangements of houses; you may find it easier to check  m  (and not  n) in ascending order and to determine the maximum  n  for each  m .  You will see that if the pair (n,m) "works" then this is also true for all pairs (n₀,m) with  n₀ < n  and all (n,m₀) with  m₀ > m , with one exeption for  m₀  at most (for certain values of  n).  –  Hint:  If  m  is checked up to  m = 4  all  n  are covered up to  n = 18 (m = 7  →  n = 30).


Solution