Neighbours This page was updated 2021-04-19. |
|
 deutsche Version deutsche Version |
Consider a village where the distances between the houses are pairwise different.
If there are n houses there will be n(n-1)/2 different distances.
The local Social Club asks all villagers to pay a visit during the following wednesday to their next neighbour.
In case that the residents of two houses have to visit each other they are requested to arrange two dates for their visits. — We will assume that on this wednesday, no other visits will be paid. — The problem presented below does not depend on the number of people living in the houses; we can assume that there is only one inhabitant in each house.
|
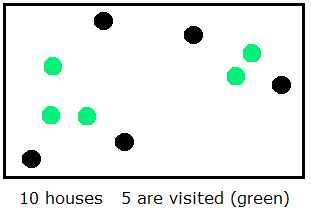 |
|
A check of some examples with few houses shows that some villagers will be visited but others will not.
How does this depend on the number n of houses?
This question shall be formulated in a more precise manner. To begin with a concrete problem: The village may consist of 7 houses; how many houses can be visited? Here we should consider possible arrangements of the houses. Can the number m of visited houses run through all values in {1, ..., 7}? Give this special problem a try to get a "feeling for the village".
The general problem: Can every m ∈ {1, ..., n} stand for the number of visited houses? We do not expect a complete solution. A good start could be the question if there are "village sizes" n for which it is impossible that all houses are visited. — One should not try endless arrangements of houses; you may find it easier to check m (and not n) in ascending order and to determine the maximum n for each m . You will see that if the pair (n,m) "works" then this is also true for all pairs (n0,m) with n0 < n and all (n,m0) with m0 > m , with one exeption for m0 at most (for certain values of n). – Hint: If m is checked up to m = 4 all n are covered up to n = 18 (m = 7 → n = 30).
Solution
The problem is special on this website insofar that we know no complete solution.
By conducting some trials one will get several special solutions for n villagers with m of them being visited. The example in the problem above with n = 7 has the following solutions:

Figure 1 n = 7 green : visited houses
The arrangements in figure 1 are not unique. We see arrangements for m ∈ {2, 3, 4, 5, 6}. For m = 7 we find no suiting arrangement. This leads to a first result for working pairs (n,m):
This can easily been proved. m = 1 is discarded because the neighbours in the two houses with minimal distance visit each other. — What about m = n ? This is obviously possible for even n as the village could be an arrangement of n/2 pairs of close-by houses. — For n odd we give an inductive proof. For n = 3 one house will not get a visit. For bigger n the two neighbours A and B with the minimal distance visit each other; the other n - 2 houses fall in one of the following two cases:
First case: At least one of the remaining n - 2 villagers visits A or B ; then there are at most n - 3 possible visitors left for n - 2 houses; thus one house at least has no visitor.
Second case: The remaining n - 2 villagers do not visit A or B ; then there are n - 2 visitors for n - 2 houses which settles the claim by induction: At least one house gets no visit.
As a preparation for the general problem figure 2 shows possible arrangements of houses for m = n - 1 (n odd) and m = n (n even):

Figure 2 m = n - 1 m = n black : house which gets no visit
⬛ m = 2 and m = 3
Some trials for pairs (n,m) leads to the conjecture that for each m there exists a maximum n . In figure 3 you see arrangements for (n,m)=(9,2) and (n,m)=(12,3).
For m = 2 resp. m = 3 you are invited to try to find bigger n than 9 resp. 12 ; such n are as yet not known.
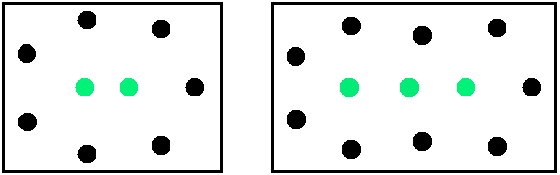
Figure 3 (n,m)=(9,2) (n,m)=(12,3) green : houses which get a visit
How are the arrangements of dots (houses) in figure 3 built? A promising method (but surely not the only one) is to make a geometric arrangement with equilateral triangles as shown in figure 3a. Then all points are moved a little bit in order to make pairwise different distances; moreover, these moves should ensure that for each black dot (standing for a house which is not visited) the nearest neighbour is green (standing for a visited house); all this is easily done, see figure 3.
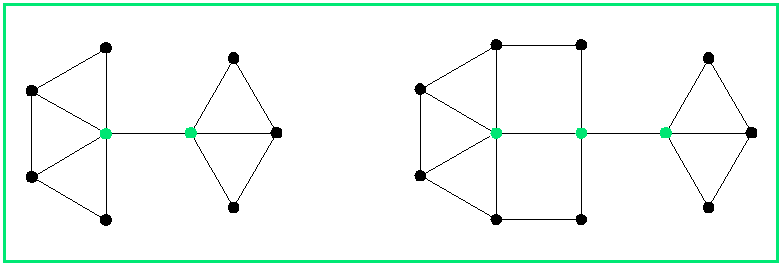
Figure 3a
⬛ m ≥ 4
We will suppose that for m = 2 and m = 3 the maximum n = 9 and n = 12 have been established. One could be tempted to proceed to m = 4, 5, ... in a similar manner. But this is unnecessary and suboptimal because one can also replicate and combine the arrangements in figure 3. We want to establish a big as possible n for each m , so it seems to be a good idea to build several "islands" of type (9,2) in figure 3 if m is even. For odd m one adds a single "island" of type (12,3). Figure 4 shows the islands for (n,m)=(57,13):
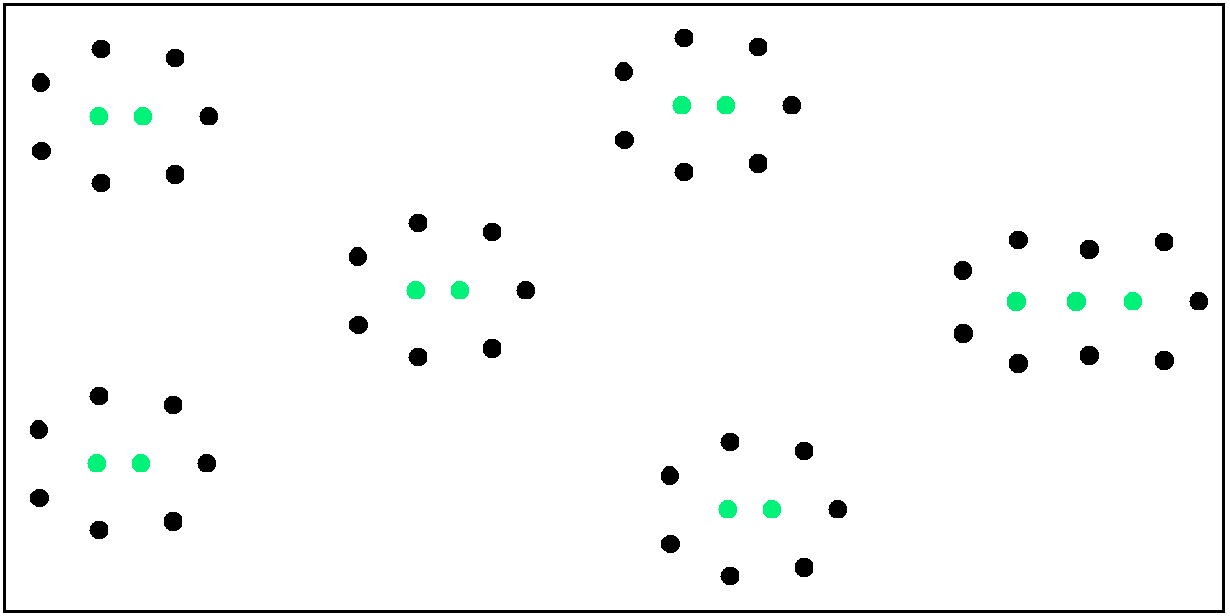
Figure 4
The combination of i islands gives the following results:
m = 2i → n = 9i
m = 2i+1 → n = 9i+3
The corresponding "anchor cells" are marked in green colour in figure 5. They stand for (n,m) with the biggest village size n known so far working with m visited houses. The other crosses stand for (n,m) which have already been confirmed as working in figures 1 and 2. The orange cells stand for m = n odd; it has been shown above that they have no working arrangement of houses.
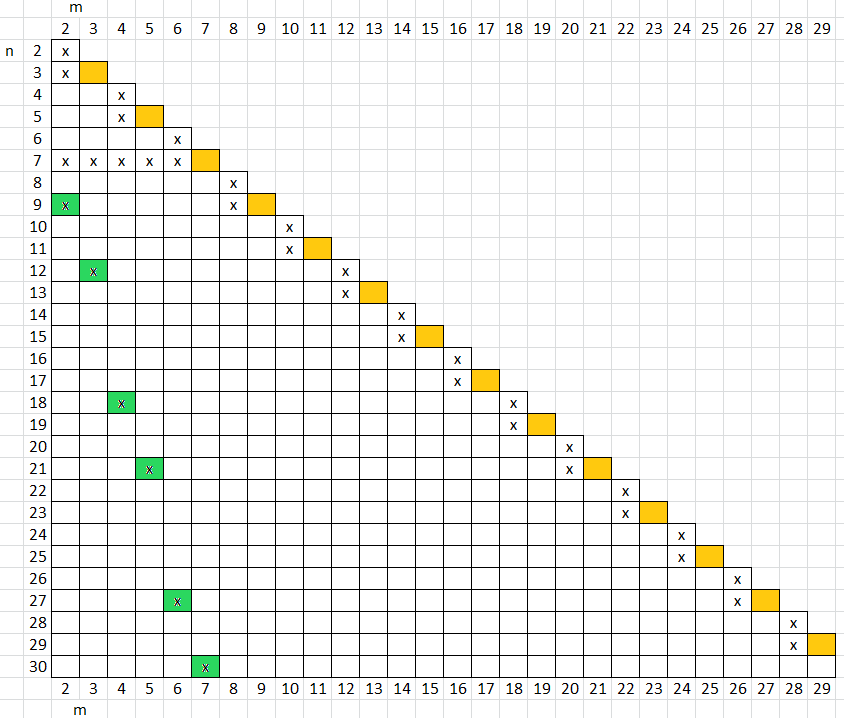
Figure 5
We want to "fill" the matrix in figure 5. It will be shown that for all m the mth column above the green anchor cells can be filled with working pairs (n,m) – up to (m,m) for even m and up to (m+1,m) for odd m . This is proved by a simple observation: In the left picture of figure 3 the black dots can be removed successively; the same applies to the picture on the right, with the exception of one black dot which has to be kept at the left edge (the middle green dot is nearer to its right neighbour than to its left one); the green dots and their distances are kept — with this procedure successively applied to all islands m stays fixed and n is reduced step by step. The removal of the black dots can be retraced by figure 4. The result is shown in figure 6:
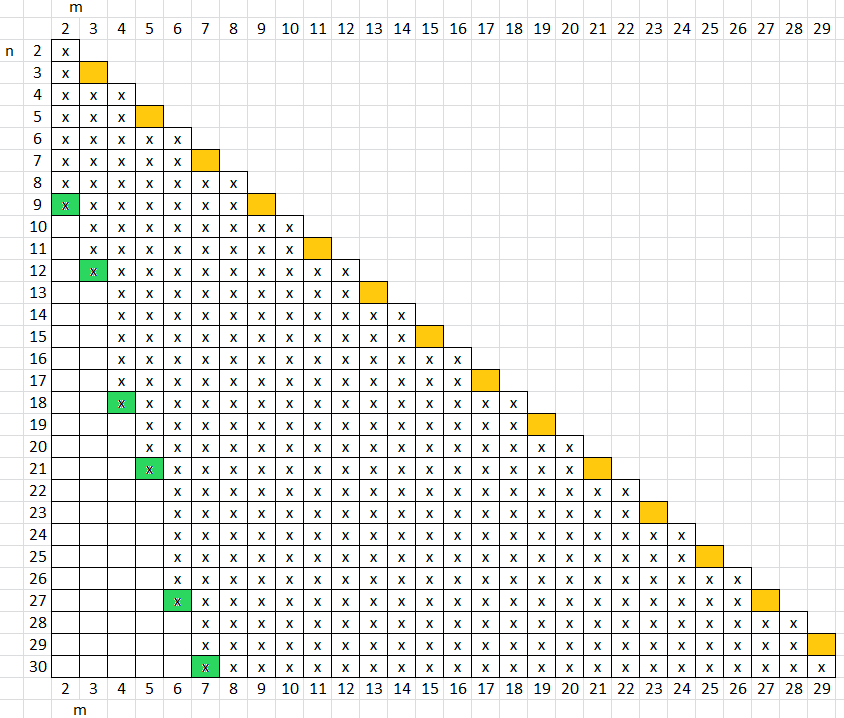
Figure 6
x: working arrangement
green: anchor cell
orange: no working arrangement
white: unproven conjecture: no working arrangement
We have shown how big n (the size of the village) can get (at least) if the number m of visited houses is known. — Example: A visit is paid to exactly 9 houses. We make the decomposition 9 = 2+2+2+3 ; each 2 stands for an arrangement of 9 houses as in the left picture in figure 3; the summand 3 stands for an arrangement of 12 houses as in the right picture in figure 3. Thus the total number of houses runs from 10 to 39 . Using the formulae above figure 5 we can present a summary for m ≥ 2 :
m even → nmin = m nmax = 9 m/2
m odd → nmin = m + 1 nmax = (9 m - 3)/2
nmax is the biggest n for which we could prove that (n,m) is a working pair. As we cannot exclude that bigger n will be found nmax is a lower bound for the "real" maximum n .
This leads to a formula for a sequence a(n) describing the minimal m depending on n :
a(2) = a(3) = 2
/ 2j for n = 9j-5 ... 9j
a(n) = j ∈ N
\ 2j+1 for n = 9j+1 ... 9j+3
All readers are invited to prove that (some of) the empty cells at the left side of figure 6 must stay empty or get a cross. To provide a general rule would be an excellent achievement – maybe this rule is the one we found for a(n).
We conclude with an example for a(n):
The village may consist of 23 houses. In case that the matrix in figure 6 is optimal we would know that at least 6 houses will be visited and at least one house will get no visit. From 6 to 22 visited houses every number can be achieved.
Whether mmin = 6 can be further reduced remains an open problem.
A347941 in OEIS a(n) in the integer sequences database
A261953 in OEIS The "inverse" sequence to a(n) in the integer sequences database
Next Neighbours in GitHub Extended version of this article with Mathematica programs
Arranging points on plane in reddit Discussion dealing with the first steps of the problem
last update 2021-11-03
previous problem | problem list
Manfred Börgens | main page
 deutsche Version
deutsche Version






