Nearest neighbours
What does this sequence represent? (2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9, 9, 9, 10, 10, 10, 10, 10, 10, 11, 11, 11, 12, 12, 12, 12, 12, 12, 13, 13, 13, 14, 14, 14, 14, 14, 14, 15, 15, 15, 16, 16, 16, 16, 16, 16, 17, 17, 17, 18, 18, 18, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 20, 21, 21, 21, 22, 22, 22, 22, 22, 22, 23, ...)
We discussed the problem of nearest neighbours in problem 114 on this website. Another version with Mathematica programs can be studied in → GitHub. A discussion dealing with the first steps of this problem appeared in → reddit.
The integer sequence resulting from the problem of nearest neighbours was published in OEIS on 1st November 2021 as A347941. The "inverse" sequence was identified as A261953.
The problem is not comprehensively solved. It deserves attention because it can be stated quite simply and seems to offer several promising ways for further investigation. We shall here present a short summary of the problem and its (as yet incomplete) solution:
Consider a set G of n points in the real plane with pairwise different distances. A point A ∈ G is called a nearest neighbour if there exists a point B ∈ G with smaller distance to A than to any other point in G.
For any given n we want to find the lowest possible number b(n) of nearest neighbours. What is already known as a (partial) solution?
- For n ≤ 9 the problem is solved: b(n) = 2 .
- For n = 10, 11, 12 we have b(n) ≤ 3 .
- For n ≥ 13 we have b(n) ≤ 2j for n = 9j-5 ... 9j and b(n) ≤ 2j+1 for n = 9j+1 ... 9j+3, j ≥ 1 .
Thereby we get a sequence a(n) as the best known upper bound for b(n) :
- a(2) = a(3) = 2 .
- a(n) = 2j for n = 9j-5 ... 9j, j ≥ 1 .
- a(n) = 2j+1 for n = 9j+1 ... 9j+3, j ≥ 1 .
This is the sequence A347941 in OEIS. A list of the entries can be seen at the top of this article. We illustrate a(n) in figures 1 and 2.
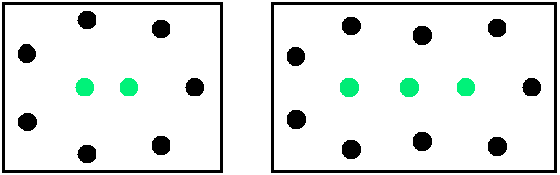
Figure 1 Green: Nearest neighbours.
Left: For n = 9 (or less) points we can find an arrangement with 2 nearest neighbours (which of course is optimal).
Right: For n = 12 (or n = 10, 11) points we can find an arrangement with 3 nearest neighbours. Does an arrangement exist for these n with 2 nearest neighbours? We suppose: No.
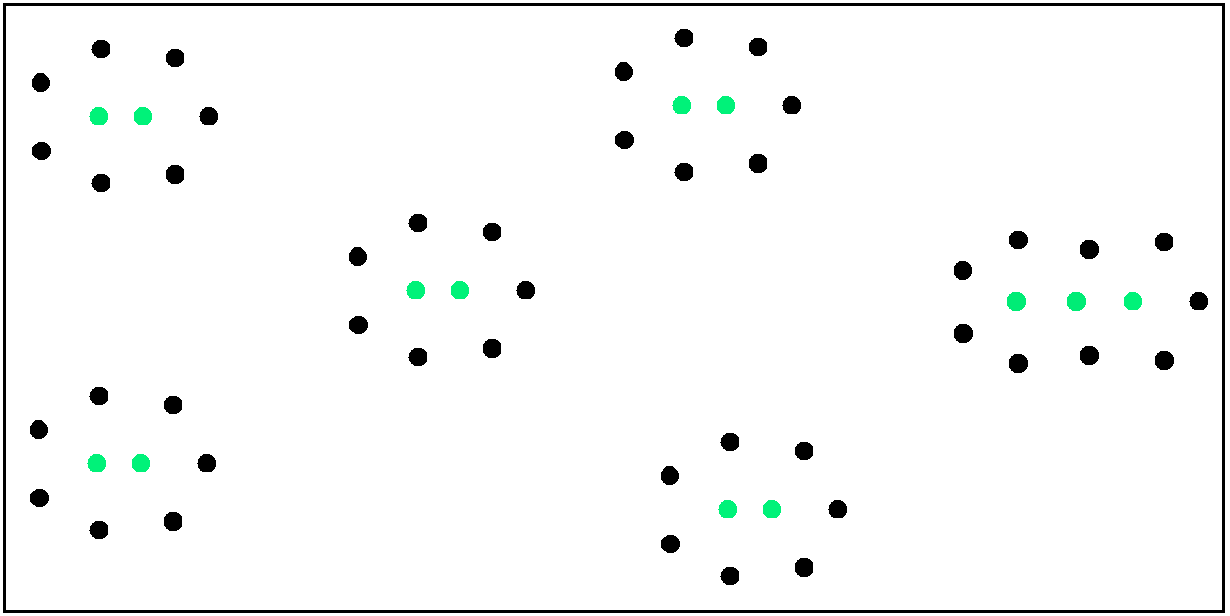
Figure 2 Green: Nearest neighbours. – For n = 57 points we can find an arrangement with 13 nearest neighbours. Does an arrangement exist for this n with less than 13 nearest neighbours? We suppose: No. This is supported by the (much tested) conjecture that combinations of several "islands" of points with 2 nearest neighbours and at most one "island" with 3 nearest neighbours give an optimal result – the islands being built as in figure 1 and arranged as in figure 2.
Figures 1 and 2 show a(9) = 2, a(12) = 3 and a(57) = 13 . The formula for the complete sequence was given above.
We can invert the problem and get a sequence c(m) in the following way:
For m nearest neighbours d(m) is defined as the largest possible number of points in G . For m ≥ 2 we obtain from a(n) the sequence c(m) = (9, 12, 18, 21, 27, 30, ...) as best known lower bounds for d(m); c(m) is listed in OEIS as A261953 für m ≥ 2 . – c(5) = 21 asserts that a G with 21 points and 5 nearest neighbours exists but no G with more than 21 points and 5 nearest neighbours is as yet known (we suppose that such a G does not exist).
Which progress with the problem of nearest neighbours seems feasible? Any comments are welcome.
- One gives a positive partial solution: b(n) = a(n) for some n > 9.
- One gives a negative partial solution: One or several conjectures made above are wrong – e.g. a G is presented with 19 points and 4 nearest neighbours. In this case a revision of a(n) would be necessary.
What would be a complete solution of the problem of nearest neighbours? Any comments are welcome.
- One gives a proof for a(9) = 2 and a(12) = 3 being optimal; and for all bigger n the "islands-method" from figure 2 is proved to be optimal. Then b(n) = a(n) is proved.
- One establishes b(n) ( ≠ a(n)) with a comprehensive and proven formula.
Last update 2021-11-02
blog overview | previous article | next article
Manfred Börgens | main page
 MB Matheblog # 15
MB Matheblog # 15 MB Matheblog # 15
MB Matheblog # 15 deutsche Version
deutsche Version
