Konstruktion des regelmäßigen Neunecks
Die Lösung steht im unteren Teil der Seite.
In Problem # 65 wurde die Konstruktion des regelmäßigen Siebenecks und des regelmäßigen Achtecks behandelt. Das regelmäßige Siebeneck lässt sich mit Zirkel und Lineal nur näherungsweise konstruieren. Aber die Baumeister und Künstler früherer Zeiten (so wie Meister Roriczer in Problem 65) waren findig darin, möglichst gute Näherungen zu ersinnen. Für das Neuneck gibt es eine Konstruktion von Albrecht Dürer, der bereits auf der Briefmarke # 95 vorgestellt wurde. Bild 1 zeigt eine andere Briefmarke mit seinem Porträt.

Bild 1 - Albrecht Dürer
1961, Michel 350, Scott 827
Ein regelmäßiges Neuneck soll in einen Kreis mit Mittelpunkt M und Radius r = MB einbeschrieben werden, siehe Bild 2. Der klassische Weg geometrischer Konstruktionen geht auf die griechische Mathematik der Antike zurück und erlaubt nur die Verwendung von Zirkel und Lineal. Offenbar reicht es aus, einen 40°-Winkel zu konstruieren. Die exakte Konstruktion dieses Winkels ist aber nicht möglich (dies wurde durch Pierre Laurent Wantzel bewiesen, siehe Briefmarke # 29). Gesucht ist also eine Konstruktion eines Winkels φ , der näherungsweise 40° beträgt. Der Winkel ∠BME zwischen den Radien MB und ME in Bild 2 beträgt näherungsweise 20°, führt also durch Verdopplung zum gewünschten Resultat. Diese und die anderen Linien in Bild 2 stammen aus einer Konstruktion von Albrecht Dürer.
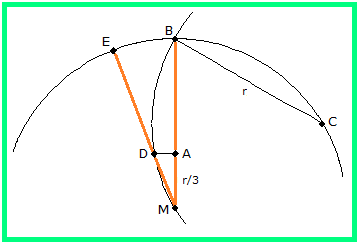
Bild 2 - Dürer-Konstruktion
Wie ist Dürer vorgegangen? Er beschreibt es im zweiten Band seiner Underweysung der Messung, mit dem Zirckel unnd Richtscheyt, in Linien, Ebnen unnd gantzen Corporen im Jahr 1525. Der Radius r wird nochmal abgetragen, von B nach C als Kreissehne. Ein zweiter Kreis wird um C geschlagen, wieder mit Radius r ; er verläuft also durch M und B . Sodann wird der Radius MB gedrittelt, dadurch erhält man den Punkt A . Dort errichtet man die Senkrechte auf MB , die den zweiten Kreis in D schneidet. Die Strecke MD wird bis E auf dem Kreis verlängert. Der Winkel φ/2 = ∠BME beträgt dann näherungsweise 20°.
Aufgabe 1
Wie exakt ist die Dürer-Konstruktion? Hier wird also nach der genauen Größe des Winkels φ gefragt.
In Howard Eves' Buch Mathematical Circles Squared wird im Abschnitt " 87 ° " eine Konstruktion des regelmäßigen Neunecks angegeben, die Ähnlichkeit zur Konstruktion von Dürer aufweist. Die einzelnen Schritte sind in Bild 3 zu sehen. Auch hier soll wieder ein Winkel φ ≈ 40° mit Zirkel und Lineal konstruiert werden.
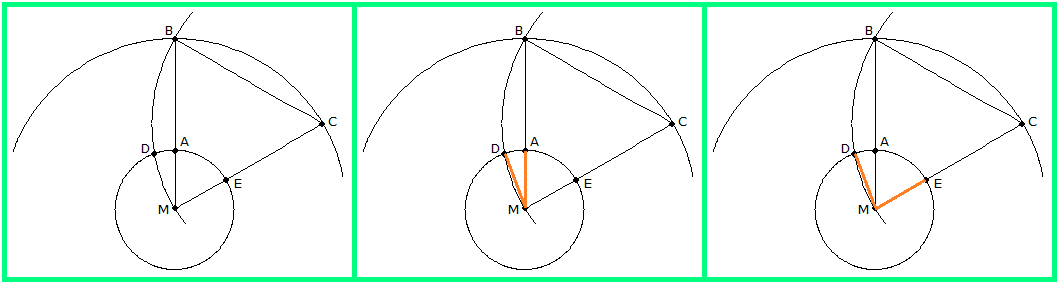
Bild 3 - Eves-Konstruktion
Eves beschreibt genau genommen zwei verschiedene, aber zusammengehörige Konstruktionen. Die Konstruktion in der mittleren Skizze von Bild 3 schreibt er Dürer zu (vielleicht wegen der Ähnlichkeit mit Bild 2), aber das erscheint fragwürdig.
Die Skizzen in Bild 3 gehen von einem Kreis mit Mittelpunkt M und Radius r1 = MA aus, in den das Neuneck eingezeichnet werden soll. Dies ist der kleine Kreis im unteren Teil der Skizzen. Man zeichnet einen zweiten, größeren Kreis um M mit Radius r2 = MB ; die genaue Größe von r2 wird später noch festgelegt.
Der Radius r2 wird nochmal abgetragen, von B nach C als Kreissehne. Man schlägt nun einen Kreisbogen um den Mittelpunkt C mit Radius r2 ; dieser verläuft durch M und B . Er schneidet den kleinen Kreis im Punkt D .
In der mittleren Skizze von Bild 3 sieht man nun das Ergebnis der ersten Konstruktion: Der Winkel φ/2 = ∠AMD beträgt (bei geeigneter Wahl von r2 ) ca. 20°, ist also der halbe Winkel, der für die Konstruktion des Neunecks benötigt wird.
Eine Variante sieht man in der rechten Skizze von Bild 3: Der Winkel 2φ = ∠EMD beträgt (bei geeigneter Wahl von r2 ) ca. 80°, ist also der doppelte Winkel, der für die Konstruktion des Neunecks benötigt wird.
Die Länge von r2 ist bisher offen geblieben und führt zu den nächsten Aufgaben.
Aufgabe 2
Eves hat r2 = 3·r1 gewählt. Wie exakt sind dann die beiden Konstruktionen? Hier wird wieder nach der genauen Größe des Winkels φ gefragt.
Aufgabe 3
Die Güte der Näherung lässt sich verbessern, wenn man in r2 = a·r1 für a einen anderen Faktor als 3 wählt. Was wäre der optimale Faktor a ? a·r1 muss aber mit Zirkel und Lineal konstruierbar sein. In Problem # 87 wurde gezeigt, wie man dafür eine Kettenbruchentwicklung einsetzen kann.
Lösung
Aufgabe 1
Wie exakt ist die Dürer-Konstruktion? Hier wird also nach der genauen Größe des Winkels φ gefragt.
Wir legen die Skizze von Bild 2 in ein cartesisches (x,y)-Koordinatensystem mit M =(0,0). Dann ist
C = (c1,c2) = (r cos 30°, r sin 30°) = (r √3/2, r/2)
Der Kreis durch M und B wird durch (x-c1)2 + (y-c2)2 = r2 beschrieben. Sein Schnittpunkt D mit der Geraden y = r/3 genügt also der Gleichung (x - r √3/2)2 + r2/36 = r2 oder |x - r √3/2| = r √35 /6 . Wegen x < 0 ist x = r(√3/2 - √35 /6).
Der gesuchte Winkel ∠BME ist gleich dem Winkel ∠AMD ; diesen Winkel bezeichnen wir mit β und erhalten tan β = DA/MA = (√35 /6 - √3/2)/(1/3). Daraus folgt für den gesuchten Winkel des Neunecks
φ = 2β = 2 arctan((√35 - 3√3)/2) ≈ 39,5941°
Das ist gegenüber dem korrekten Winkel von 40° eine Abweichung von ca. 1% . Wenn man diesen Winkel neun Mal auf dem Kreis abträgt, fehlen am Ende ca. 3,65°. Die Dürer-Konstruktion ergibt also keine besonders gute Näherung.
Aufgabe 2
Eves hat r2 = 3·r1 gewählt. Wie exakt sind dann die beiden Konstruktionen? Hier wird wieder nach der genauen Größe des Winkels φ gefragt.
Bild 4 enthält den Ansatz für die Winkelberechnung.
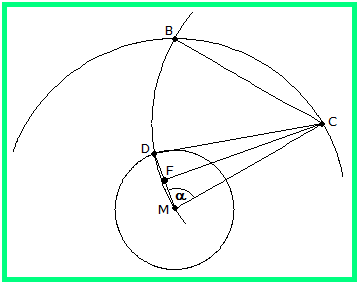
Bild 4
Bild 4 beruht auf der linken Skizze von Bild 3. Wir wollen zunächst den Winkel α im Dreieck Δ MCD berechnen. Dazu halbieren wir die Seite MD . MF hat dann die Länge r1/2 . Δ MCF ist ein rechtwinkliges Dreieck mit cos α = (r1/2)/r2 . Also gilt:
(1) α = arccos(r1/(2r2))
a) Konstruktion von φ mit ∠AMD (mittlere Skizze in Bild 3)
(2) φ = 2∠AMD = 2(α-60°) = 2 arccos(r1/(2r2))-120°
Mit r2 = 3·r1 ergibt sich φ = 2 arccos(1/6) - 120° ≈ 40,8119°.
Das ist ein noch schlechteres Ergebnis als das von Dürer. Die Abweichung gegenüber dem korrekten Winkel von 40° beträgt ca. 2% . Wenn man diesen Winkel neun Mal auf dem Kreis abträgt, hat man am Ende ca. 7,3° mehr als der Vollkreis.
b) Konstruktion von φ mit ∠EMD (rechte Skizze in Bild 3)
(3) φ = (1/2)∠EMD = (1/2)∠CMD = α/2 = (1/2) arccos(r1/(2r2))
Mit r2 = 3·r1 ergibt sich φ = (1/2) arccos(1/6) ≈ 40,2030°.
Das ist das beste der bisherigen drei Ergebnisse. Die Abweichung gegenüber dem korrekten Winkel von 40° beträgt ca. 0,5% . Wenn man diesen Winkel neun Mal auf dem Kreis abträgt, hat man am Ende ca. 1,8° mehr als der Vollkreis.
Aufgabe 3
Die Güte der Näherung lässt sich verbessern, wenn man in r2 = a·r1 für a einen anderen Faktor als 3 wählt. Was wäre der optimale Faktor a ? a·r1 muss aber mit Zirkel und Lineal konstruierbar sein. In Problem # 87 wurde gezeigt, wie man dafür eine Kettenbruchentwicklung einsetzen kann.
Für eine exakte Konstruktion des 40°-Winkels müsste α in Bild 4 80° betragen. Dann würden beide Konstruktionen a) und b) aus Aufgabe 2 φ = 40° ergeben. Aus (1) ergibt sich dann für den optimalen Faktor a :
a = r2/r1 = (2 cos 80°)-1 ≈ 2,879385
Auf die reelle Zahl 2,879385... wenden wir das Kettenbruchverfahren aus Problem # 87 an und erhalten als Näherungen dieser Zahl die gegen a konvergente rationale Zahlenfolge
2, 3, 23/8, 72/25, 167/58, ...
In Mathematica erhält man beispielsweise den dritten Bruch 23/8 mit
FromContinuedFraction[ContinuedFraction[2.879385, 3]].
Mit a = r2/r1 erhalten wir α = arccos(1/(2a)). α wird dann in (2) bzw. (3) eingesetzt; wir erhalten also
φ = 2 arccos(1/(2a)) - 120° in (2)
φ = (1/2)arccos(1/(2a)) in (3)
Es folgt eine Tabelle, die alle Ergebnisse zusammenfasst. Für a wurden die beiden ersten Brüche aus der Kettenbruchentwicklung genommen, also 23/8 und 72/25 . Für die Konstruktion von r2 = (23/8)r1 muss man dreimal eine Strecke halbieren, um r1/8 zu erzeugen; r1/8 muss dann 23-mal abgetragen werden (oder man vermindert für den Faktor 23/8 die dreifache Strecke um ein Achtel). Das ist schon mühsam genug, erscheint aber noch machbar. a = 72/25 erfordert zweimal die Fünfteilung einer Strecke, um r1/25 zu erzeugen; diese Strecke muss dann 72-mal abgetragen werden. Das wird man allein schon deshalb nicht tun (und erst recht nicht die weiteren Brüche wie 167/58 für a verwenden), da aus der Tabelle ersichtlich ist, dass bereits 23/8 eine hervorragende Näherung von φ ≈ 39,9923° ergibt.
| |
a |
φ |
Abweichung |
| Dürer |
|
39,5941° |
- 1 % |
| Eves (a) |
3 |
40,8119° |
+ 2 % |
| |
23/8 |
39,9692° |
- 0,08 % |
| |
72/25 |
40,0043° |
+ 0,01 % |
| Eves (b) |
3 |
40,2030° |
+ 0,5 % |
| |
23/8 |
39,9923° |
- 0,02 % |
| |
72/25 |
40,0011° |
+ 0,003 % |
Publiziert 2018-03-30 Stand 2015-11-28
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite



