
Deutschland 2006 Michel 2531
Albrecht Dürer (1471 - 1528)
Albrecht Dürer verdankt seinen Ruhm in erster Linie seinem künstlerischen Werk. Zahlreiche seiner Holzstiche, Kupferstiche und Gemälde sind weltbekannt und waren schon auf mehreren deutschen Banknoten zu sehen. Schaut man sich jedoch seine umfangreichen Schriften an, so wird deutlich, dass sich Dürer selbst auch als Mathematiker sah. Der größere Teil seiner Bücher befasst sich mit Geometrie. In der Renaissance gewann die Mathematik in der Kunst große Bedeutung, vor allem durch die Lehre von Proportion und Perspektive. Dürer war einer der wichtigsten Vertreter dieser neuen mathematisch durchdrungenen Kunst, zusammen mit den italienischen Renaissance-Malern wie Leonardo da Vinci und Raffael. Dürer kaufte 1507 in Venedig die Elemente des Euklid in lateinischer Übersetzung; sein Exemplar enthielt wohl die erste vollständige Übersetzung aus dem Griechischen, die in gedruckter Form erschien.
Auch sein Arnheimer Verleger Johan Jansen nannte Dürers Gesammelte Werke von 1604:
Alle Bücher des weitberühmbten und künstreichen Mathematici und Mahlers Albrechten Durers von Nürenberg
Das Titelblatt sieht man links in Bild 1. Amüsant ist die Nennung der Zielgruppe dieses Werks:
Allen Mahlern, Steinmetzern, Bildthäwern und Schnitzern, Goldtschmiden, Baw- und Bergmeistern, Feldtherrn, Kriegsobristen, Hauptleuthen, Befelchhabern, Büchsenmeistern und dergleichen Kunstliebhabern

Bild 1 aus Dürers Gesammelten Werken
Neben dem Titelblatt sieht man in Bild 1 drei ausgewählte Seiten mit geometrischen Skizzen. Die mathematischen Abhandlungen Dürers befassen sich vor allem mit vier Gebieten: ebene und räumliche Kurven, Polygone und Polyeder, Perspektive, Baukunst. In allen diesen Gebieten legt Dürer den Schwerpunkt auf die Konstruktion.
Auf dem zweiten Blatt in Bild 1 sieht man die Konstruktion der Hyperbel als Kegelschnitt. Auf dem dritten Blatt konstruiert Dürer die Pascalsche Schnecke, die eigentlich seinen Namen tragen müsste, da er sie ca. 50 Jahre vor Blaise Pascals Vater Étienne Pascal entwarf. Das vierte Blatt zeigt den Schneck, eine räumliche Spirale.
Die Skizzen in Bild 1 sind dem ersten Band der Underweysung der Messung, mit dem Zirckel unnd Richtscheyt, in Linien, Ebnen unnd gantzen Corporen entnommen. Dieses Werk von 1525 ist das früheste Geometriebuch in deutscher Sprache. In diesem und den drei weiteren Bänden erklärt Dürer eine Vielzahl mathematischer Kurven (u.a. die Logarithmische Spirale und die Epizykloide), gibt exakte und genäherte Methoden zur Herstellung regulärer Polygone an, stellt die Platonischen und Archimedischen Körper vor, und analysiert Probleme der Perspektive und des Schattenwurfs.
Der Kupferstich Melencolia I gilt als ein Meisterwerk Dürers. Wir schauen uns zuerst dieses Bild auf einer Briefmarke (Teil eines Blocks) an:

Mongolei 1978 Michel 1184 Scott 1039
Ein gutes hochauflösendes Bild zeigt die Vielzahl mathematischer Bezüge in der Melencolia: Zirkel, Kugel, Polyeder, magisches Quadrat, Zentralprojektion. Bild 2 zeigt eine Vergrößerung des magischen Quadrats, das in allen Zeilen, Spalten und Diagonalen die Summe 34 aufweist; die beiden mittleren Felder in der untersten Zeile zeigen 1514, das Jahr der Erstellung der Melencolia.

Bild 2
Das Polyeder links in der Melencolia hat viele Rätsel aufgegeben; davon zeugen zahlreiche Veröffentlichungen (siehe in der englischen Wikipedia Truncated triangular trapezohedron), die sich vor allem mit der Größe der Winkel auf dem Körper und der Existenz einer Umkugel befassen. In einem Skizzenbuch Dürers findet sich der Ursprung dieses Details der Melencolia, siehe Bild 3:
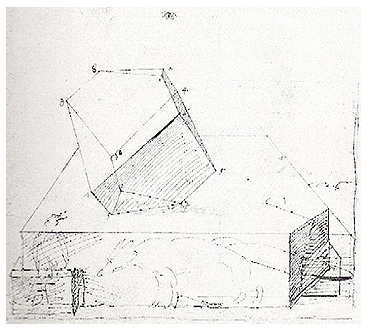
Bild 3
Es ist erstaunlich, dass die Angaben über die Winkel der Seitenflächen weit auseinander liegen. Aber obwohl man davon ausgeht, dass sich das Polyeder korrekt in die Zentralprojektion einfügt, sind seine Maße offenbar nicht eindeutig rekonstruierbar. Weitgehende Einigkeit unter den Gelehrten besteht aber im folgenden Punkt: Es handelt sich um ein abgestumpftes Rhomboeder. Ein Rhomboeder ist ein sehr regelmäßiger Körper, der sechs gleiche Rauten als Seitenflächen hat. Von diesem Körper wurden an den Enden der längsten Achse zwei gegenüberliegende Ecken abgeschnitten (Bild 4, mit anderen (etwas länglicheren) Rauten als im Dürer-Polyeder). Auf diese Weise entstehen zwei gleichseitige Dreiecke als neue Seiten; aus den Rauten werden Fünfecke.
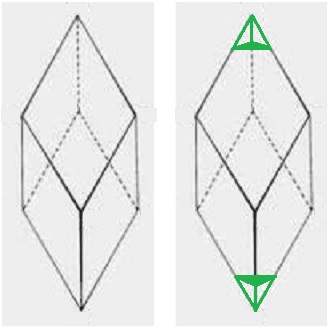
Bild 4 Rhomboeder
Dürers Skizze des Polyeders ist gegenüber der Darstellung in der Melencolia spiegelverkehrt, was sich aus der Technik des Kupferstichs leicht erklären lässt. Dass es sich tatsächlich um die gleichen Polyeder handelt, sieht man in Bild 5. Dort wurde die Skizze gespiegelt (linkes Bild) und dem Polyeder in der Melencolia überlagert (rechts). Das passt haargenau, und eine Analyse der Perspektive tut ein Übriges, um Dürers Vorgehen zu erhellen: In der Skizze links sind die Kanten des Fundaments orange eingefärbt; diese Linien wurden in das rechte Bild übertragen, gemäß einer Zentralprojektion zum Horizont verlängert (grün) und treffen dort genau den Fluchtpunkt des Bildes, wie man an den anderen grünen Geraden erkennt (die sich aus den Gebäudekanten in der Melencolia ergeben). Dürer hat also offenbar die später verwendete Perspektive schon in der Skizze des Polyeders im Sinn gehabt.
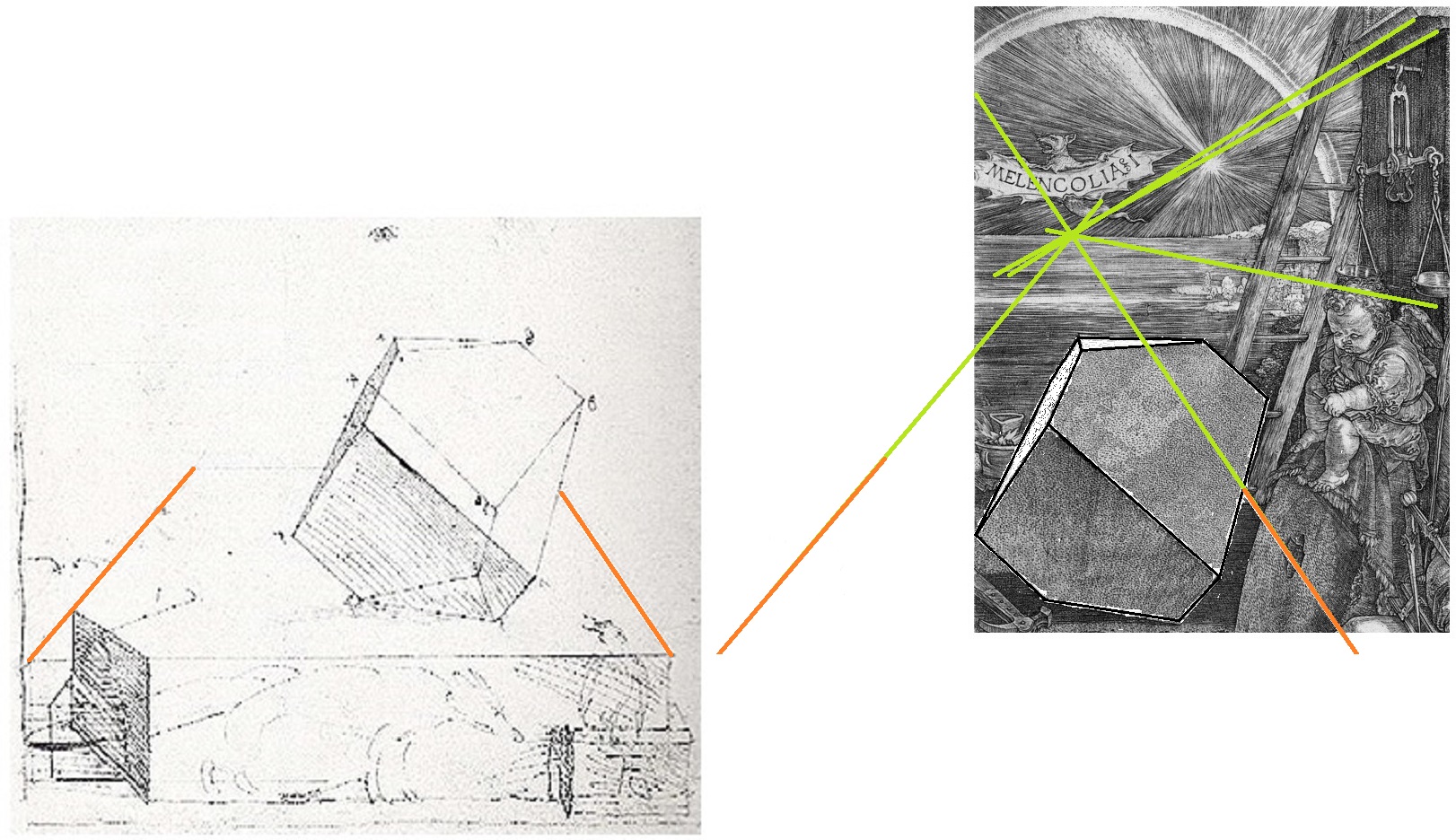
Bild 5 links Vorarbeit zu Melencolia aus Dürers Skizzenbuch (gespiegelt), rechts Überlagerung der Skizze auf das Polyeder im Kupferstich
Die exakte Beschreibung des Dürer-Polyeders setzt natürlich voraus, dass man sich auf die Form der Rauten einigt. Etliche Quellen geben die Rautenwinkel mit 72° und 108° an; sie gehen außerdem davon aus, dass die Kappung der beiden Rhomboederecken von Dürer gerade so vorgenommen wurde, dass das Polyeder eine Umkugel hat (also alle Ecken auf einer Kugel liegen). Diese Auffassung findet sich in der deutschen Wikipedia, wo auch alle Maße des Polyeders aufgeführt sind, in der Mathematik-Enzyklopädie MathWorld unter "Dürer's Solid" und im CAS Mathematica, wo sich das Polyeder mit PolyhedronData["DuerersSolid"] erzeugen lässt.
Ein "optisches" Argument für das 72°-Umkugel-Polyeder gibt Yvo Jacquier mit seinem Modell, das in Bild 6 dem Dürer-Polyeder gegenübergestellt wird. - Andere Wissenschaftler haben aber auch größere Winkel als 72° postuliert, unter anderem (mit ausführlicher mathematischer Begründung) Eberhard Schröder in Dürer, Kunst und Geometrie. 2019 erschien die Arbeit Rekonstruktion des Polyeders in A. Dürers Kupferstich MELENCOLIA I von J. Fertl und E.T. Mayer, in der der Winkel mit 78,0° bzw. 78,4° angegeben und hergeleitet wird. Die Konstruktion des Polyeders erlaubt in diesem Fall nicht die Existenz einer Umkugel.

Bild 6 © Yvo Jacquier
In Bild 7 sieht man das Polyeder eingebettet in seine Umkugel, aus zwei Perspektiven:
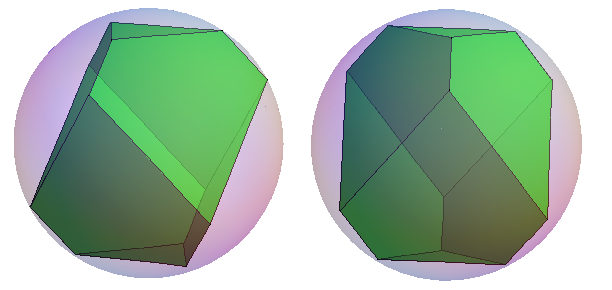
Bild 7 Dürer-Polyeder mit Umkugel
Mathematica gibt den Umkugelradius mit R = (17 + 7·√5)1/2/√8 an. Wie kommt das zustande? Dieses R ergibt sich, wenn man für die kürzeste Kante des Polyeders die Länge b = 1 annimmt. In den Formelsammlungen wird dagegen a für die längste Kante zugrunde gelegt. Für die Umrechnung benötigt man:
(*) b = a(3 - √5)/2 R = a(14 - 2·√5)1/2/4
Mit b = 1 ist a = (3 + √5)/2 und R = ((14 - 2·√5)(14 + 6·√5))1/2/8 = (136 + 56·√5)1/2/8 = (17 + 7·√5)1/2/√8 .
Etwas näherliegend erscheint allerdings, dass man als Radius der Umkugel R = 1 nimmt und dann die Kantenlängen des Polyeders berechnet. Außer den Kantenlängen a und b ist noch c als Länge der Dreiecksseiten anzugeben. Aus der Formelsammlung erhält man c = a(5 - 2·√5)1/2 . Damit und mit (*) ergeben sich die Kantenlängen:
a = (14 + 2·√5)1/2/√11 ≈ 1,296 b = (17 - 7·√5)1/2·√(2/11) ≈ 0,495 c = (25 - 9·√5)1/2·√(2/11) ≈ 0,942
→ Dürers Neuneck in Problem # 102