
Michel 2215
Scott 1811
| Manfred Börgens Mathematik auf Briefmarken # 29 |
Liste aller Briefmarken vorige Marke nächste Marke |
zur Leitseite |
 |
DDR 1977 Michel 2215 Scott 1811 |
Carl Friedrich Gauß (1777 - 1855)
mit 17-Eck, Lineal und Zirkel
Die DDR hat diese Briefmarke anlässlich des 200. Geburtstags von Carl Friedrich Gauß herausgegeben. Auch hier wird sie zu seinem Geburtstag, dem 30. April, gezeigt. Ungewöhnlich ist, dass Gauß als junger Mann porträtiert ist, aber das hat einen besonderen Grund: Auf der Marke ist ein regelmäßiges 17-Eck abgebildet, und Gauß bewies schon als 19-jähriger, dass die Konstruktion dieses Polygons nur mit Zirkel und (unmarkiertem) Lineal möglich ist.
(Im folgenden ist "Konstruktion" immer in diesem Sinne gemeint.)
Gauß war auf diese Entdeckung sehr stolz, denn sie stellte den ersten Fortschritt auf dem Gebiet der regelmäßigen n-Ecke seit der Antike dar.
(Im folgenden wird kurz "n-Eck" für "regelmäßiges n-Eck" geschrieben.)
Welche n-Ecke konnte man vor Gauß konstruieren? Im Wesentlichen waren das lediglich Dreieck, Viereck (Quadrat) und Fünfeck. Diese "klassischen" Konstruktionen beruhten auf der Kenntnis, wie man die zugehörigen Winkel von 60°, 90°, 108° konstruiert; äquivalent dazu ist die Konstruktion der zugehörigen Mittelpunktswinkel 120°, 90°, 72° . Das ist für das Fünfeck (siehe Skizze) nicht ganz einfach (Konstruktionsanleitung).
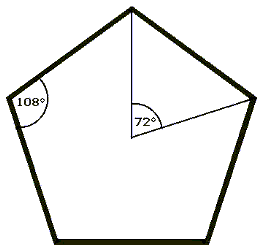
Für ein n-Eck gilt allgemein:
Eckwinkel = ( 1 - 2/n ) · 180°, Mittelpunktswinkel = 360°/ n
Aus Dreieck, Viereck und Fünfeck gewinnt man leicht eine Vielzahl anderer n-Ecke. Indem man die Mittelpunktswinkel von Dreieck und Fünfeck überlagert, erhält man ihre Differenz 48°, durch Halbierung dieses Winkels 24° und auf diese Weise ein 15-Eck mit Eckwinkel 156°. Durch (wiederholte) Halbierung der Mittelpunktswinkel ließen sich somit (schon seit der Antike) n-Ecke für folgende n konstruieren:
n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24 usw.
Aber in dieser Zahlenfolge fehlen wichtige Fälle wie n = 7, 9, 11 usw.
Gauß bewies 1796, dass 3 und 5 Spezialfälle einer allgemeinen Regel sind: Ist n eine "Fermat'sche Zahl", d.h. von der Form
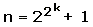
für eine ganze Zahl k , und ist n außerdem eine Primzahl, so lässt sich ein n-Eck konstruieren. Gauß war also der erste, der die Möglichkeit einer solchen Konstruktion für n = 17, 257, 65537 (alles Fermat'sche Primzahlen) nachweisen konnte.
Man kennt auch konkrete - mit wachsendem n aufwändigere - Konstruktionsvorschriften für diese n-Ecke.
Analog zum 15-Eck gilt auch hier, dass man durch Multiplikation verschiedener Fermat'scher Primzahlen weitere Zirkel-und-Lineal-Konstruktionen erhält, also z.B. für n = 51 ( = 3·17 ) oder für n = 255 ( = 3·5·17 ) .
Denn man weiß aus der Zahlentheorie, dass es für zwei teilerfremde natürliche Zahlen n1, n2 immer ganzzahlige Faktoren a1, a2 gibt mit a1·n1 + a2·n2 = 1 , woraus a2/n1 + a1/n2 = 1/(n1·n2) folgt. Kann man also das n1-Eck und das n2-Eck konstruieren, so erhält man auf diese Weise mit Hilfe der Mittelpunktswinkel das (n1·n2)-Eck. Will man etwa das 51-Eck konstruieren ( n1 = 3, n2 = 17 ) , so sind a1 = 6, a2 = -1 , also bildet man die Differenz des 6-fachen Mittelpunktswinkels des 17-Ecks und des Mittelpunktswinkels des Dreiecks: ( 6/17 - 1/3 )·360° = ( 1/51 )·360° . Dieses Verfahren lässt sich für mehr als zwei teilerfremde Faktoren fortsetzen, z.B. für n = 255 = 5·51 ( = 5·3·17 ) .
Außerdem lassen sich die Mittelpunktswinkel fortgesetzt halbieren; also folgt aus der Konstruierbarkeit des n-Ecks auch die des (2k·n)-Ecks.
Pierre Laurent Wantzel bewies 1836, dass auch die Umkehrung der Gauß'schen Entdeckung gilt, nämlich dass aus der Konstruierbarkeit des regelmäßigen n-Ecks folgt, dass die Primfaktorzerlegung von n nur eine Potenz von 2 und verschiedene Fermat'sche Primzahlen enthält.
Also lässt sich ein n-Eck genau dann konstruieren, wenn
n = 2k·p1·...·pr
mit verschiedenen Fermat'schen Primzahlen pi .
Ist damit das Problem der Konstruierbarkeit von n-Ecken gelöst?
Nein.
Denn niemand weiß, ob es über die fünfte Fermat'sche Primzahl
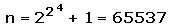
hinaus weitere Fermat'sche Primzahlen gibt. Die nächsten 28 folgenden Fermat'schen Zahlen

sind (bis 2003) als nicht-prim nachgewiesen worden; für k = 33 weiß man es nicht (Stand 10/2015; über den aktuellen Stand der Suche nach Fermat'schen Primzahlen kann man sich hier informieren).
Man kennt 32 "Grundkonstruktionen" für n-Ecke, aus denen alle anderen durch (fortgesetzte) Verdoppelung der Eckenzahl hervorgehen. Sie kommen durch Multiplikation der bekannten Fermat'schen Primzahlen zustande, unter Hinzunahme von n = 4 :
3
4
5
15
17
51
85
255
257
771
1.285
3.855
4.369
13.107
21.845
65.535
65.537
196.611
327.685
983.055
1.114.129
3.342.387
5.570.645
16.711.935
16.843.009
50.529.027
84.215.045
252.645.135
286.331.153
858.993.459
1.431.655.765
4.294.967.295
Für genau 24 Zahlen n unter 100 lässt sich ein n-Eck konstruieren:
3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, 32, 34, 40, 48, 51, 60, 64, 68, 80, 85, 96
Weitere Gauß-Briefmarke
Kategorie: Zahlen und Zahlsysteme, Berechnung von π