Wie Meister Roriczer Sieben- und Achtecke konstruierte.
Der Regensburger Dombaumeister Matthäus Roriczer (ca. 1430 - ca. 1495) hat das Büchlein Geometria deutsch geschrieben. In ihm sind die Lösungen mehrerer elementarer geometrischer Probleme enthalten, die wichtig für den Kirchenbau sind. Dabei kommt es Roriczer vor allem auf möglichst elegante Konstruktionsvorschriften an, die von den Architekten und Handwerkern an den Dombauhütten mit einfachen Mitteln umgesetzt werden konnten. Regelmäßige Vielecke wurden u.a. beim Bau von Kirchenfenstern benötigt. Zwei schöne Konstruktionen solcher Polygone wollen wir uns anschauen.
Konstruktion eines regelmäßigen Achtecks in ein vorgegebenes Quadrat
Das Achteck soll nicht mit vier Ecken die Quadratseiten berühren, sondern vier seiner Seiten sollen mittig auf den Quadratseiten liegen, so wie in Bild 1a:
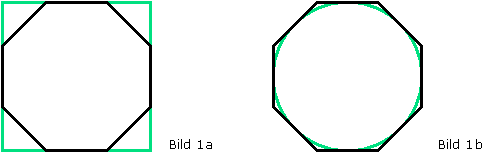
Wenn man ausrechnet, wo die Eckpunkte des Achtecks liegen, weiß man auch, wie Meister Roriczer mit einer einzigen und sehr einfachen Zirkeleinstellung diese Punkte einzeichnen konnte. Wer eine Hilfe braucht, kann den Originaltext lesen, der aber in altem und etwas schwer verständlichem Deutsch verfasst ist (in der Lösung wird eine Übersetzung gegeben).
Wie hat Meister Roriczer das regelmäßige Achteck konstruiert ?
Warum ist die Konstruktion des Achtecks in ein Quadrat äquivalent zur Konstruktion um einen Kreis (siehe Bild 1b) ?
Konstruktion eines regelmäßigen Siebenecks in einen vorgegebenen Kreis
Wer ein wenig über die Konstruktion regelmäßiger Polygone weiß, wird an dieser Stelle stutzig. Denn man kann beweisen, dass die Konstruktion des regelmäßigen Siebenecks (Bild 2a) mit Zirkel und Lineal unmöglich ist. (Mehr Informationen dazu findet man auf der Briefmarkenseite über Carl Friedrich Gauß.) Matthäus Roriczer gibt aber in der Geometria deutsch eine einfache und schöne Konstruktion an. Man kann sie sich im Originaltext anschauen (in der Lösung wird eine Übersetzung gegeben), aber vermutlich reicht schon ein Blick auf seine Zeichnung (siehe Bild 2b):
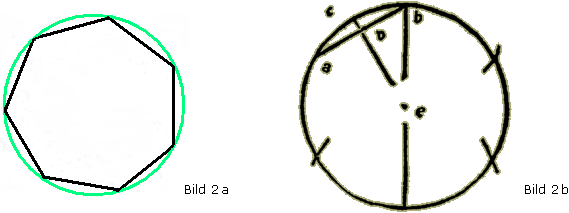
Wie hat Meister Roriczer das (fast) regelmäßige Siebeneck konstruiert ?
Wie genau ist diese Näherungslösung ?
Warum ist für alle regelmäßigen n-Ecke die Konstruktion in einen Kreis äquivalent zur Konstruktion um einen Kreis ?
(Dies erweitert auch die Äquivalenzaufgabe aus dem Abschnitt über das Achteck oben.)
Ein weiteres geometrisches Problem steht bei der Briefmarke # 65.
Lösung