Ein altes Problem und der PERELMANsche Papiercomputer
Eine schon lange bekannte Problemstellung lautet beispielhaft so:
Aus einem Wasserbehälter sollen 3 Liter entnommen werden. Es sind aber nur zwei Krüge mit 7 bzw. 9 Liter Volumen zur Hand.
Wir haben es also mit der Klasse der Umfüllprobleme zu tun. Durch eine endliche Anzahl von Umfüllvorgängen zwischen dem Wasserbehälter und den beiden Krügen (die natürlich keine Skalen zur Ablesung eines Teilvolumens aufweisen) soll eine vorgegebene Menge abgemessen werden. Natürlich sind die Volumina 3, 7, 9 willkürlich gewählt und können ganz andere Werte annehmen. Das gewählte Beispiel ist nicht ganz einfach, immerhin benötigt man acht Umfüllvorgänge, um 3 Liter abzumessen. Unterstellt wird dabei, dass der Behälter genügend viel Wasser enthält, das heißt in der Regel mindestens soviel, wie in beide Krüge zusammen passt. Manchmal findet man aber solche Probleme auch in der abgewandelten Form, dass der Behälter ein dritter Krug mit bekanntem Volumen ist.
Wie löst man ein solches Problem? In Büchern mit mathematischen Rätseln werden fast immer nur die einzelnen Umfüllschritte angegeben, aber es wird nicht klar, ob die Lösung die kürzeste ist oder sogar eindeutig; vor allem ist meist keine Systematik erkennbar. Man hat den Eindruck, dass es auf Intuition oder geschicktes Ausprobieren ankommt. Tatsächlich ist das aber nicht so: Es gibt im wesentlichen nur einen Lösungsweg, und die einzelnen Umfüllschritte folgen einer sehr einfach zu merkenden Regel.
Hier kommt der weißrussische Wissenschaftler Yakov Isidorovich Perelman (1882 - 1942) ins Spiel. Perelman studierte Forstwissenschaften in St. Petersburg und erhielt dort eine fundierte Ausbildung in Mathematik und den Naturwissenschaften. Ab 1918 arbeitete er für die sowjetrussische Nationale Kommission für Ausbildung. Sein lebenslanges Hauptinteresse lag in der Vermittlung von Mathematik, Astronomie, Physik und Technik für ein breites Publikum. Perelmans Bibliographie umfasst Hunderte von Fachartikeln und Büchern. Sein schriftstellerischer Erfolg beruhte auf seiner Fähigkeit, wissenschaftliche Inhalte verständlich und fesselnd darzustellen. Populärwissenschaftliche Publikationen wie z.B. "Algebra zur Unterhaltung" und "Lebendige Mathematik" haben bis heute zahllose Auflagen erlebt und sind in viele Sprachen übersetzt worden.
 Y. I. Perelman
Y. I. Perelman
Yakov Isidorovich Perelman darf nicht mit einem anderen russischen Mathematiker verwechselt werden. Sein Namensvetter - aber nicht mit Yakov verwandt - Grigorij Yakovlevich Perelman (geb. 1966) ist einer der renommiertesten Mathematiker der Gegenwart, weil er die Poincaré'sche Vermutung bewiesen hat. Am 22. August 2006 wurde ihm auf dem Internationalen Mathematiker-Kongress in Madrid die Fields-Medaille verliehen. G. Y. Perelman, der als höchst exzentrisch gilt, erschien nicht zum Kongress und lehnte die Ehrung ab.
Schon zu Y. I. Perelmans Zeiten war das Umfüllproblem nicht neu. Aber er hatte eine gute Idee. Er stellte das Problem und seine Lösung auf geschickte Weise graphisch dar. Wir wollen die folgende Notation einführen: n bzw. m (Liter) seien die (ganzzahligen) Volumina der beiden Krüge, k die (ganzzahlige) abzumessende Menge. Mit (a,b) bezeichnen wir den jeweiligen Füllungsstand der beiden Krüge. Man beginnt also bei (0,0) und hat als Ziel (k,b) oder (a,k). Perelman zeichnete nun alle Füllungsstände (a,b) mit ganzzahligen 0 ≤ a ≤ n und 0 ≤ b ≤ m als Gitternetz in ein Koordinatensystem. Aus Gründen, die wir noch erkunden werden, ist sein Koordinatensystem aber nicht rechtwinklig, sondern die positiven Achsen bilden einen Winkel von 60°. So sieht das Gitternetz für n = 5 und m = 3 aus:
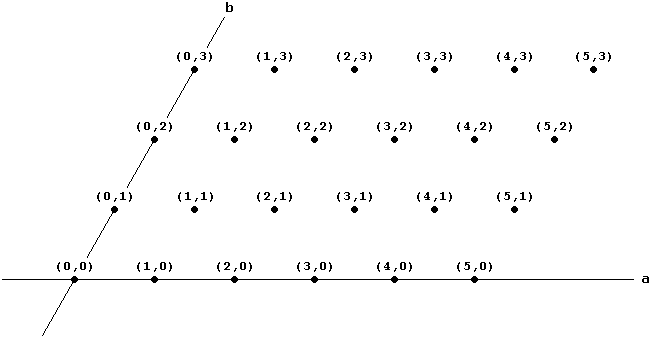
Die Punkte in diesem Gitternetz werden jetzt so verbunden, dass ein Raster aus gleichseitigen Dreiecken entsteht. Man beachte, dass jede gerade Linie von Rand zu Rand einem Umfüllvorgang entspricht (grüne Linie im nächsten Bild als Beispiel). Dieses Gebilde nennen wir Perelman'scher Papiercomputer, denn er wird uns alle Arbeit bei der Lösung des Umfüllproblems abnehmen. Die Beschriftung der inneren Punkte lassen wir ab jetzt fort, denn wir werden noch sehen, dass sie später nicht mehr benötigt werden.
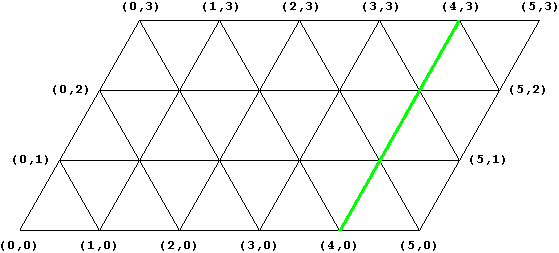
Genau genommen entspricht die grüne Linie zwei Umfüllvorgängen: Von unten links nach oben rechts wird der leere kleine Krug aus dem Behälter gefüllt (mit 3 Litern), von oben rechts nach unten links wird er in den Behälter entleert; in beiden Fällen bleibt der große Krug mit 4 Litern Inhalt unverändert.
Wie funktioniert nun dieser Papiercomputer?
Beginnend bei (0,0), geht man zu (0,3) oder zu (5,0) und von dort auf einem Zickzackweg, immer entlang gerader Linien von Rand zu Rand, bis man an einem Punkt angekommen ist, der die abzumessende Menge k darstellt. Der Grund für die 60°-Neigung der senkrechten Achse wird jetzt deutlich: Stößt man im Papiercomputer an einen Rand, so verläuft der weitere Weg nach dem optischen Prinzip "Einfallswinkel = Ausfallswinkel" (dieser Winkel ist hier immer 60°).
Ein Beispiel: Die beiden Krüge fassen 5 bzw. 3 Liter; 4 Liter sind abzumessen:
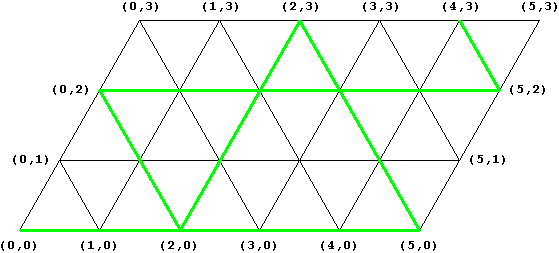
Papiercomputer löst n = 5, m = 3, k = 4
Wir führen eine Notation für die Umfüllschritte ein:
G großer Krug
K kleiner Krug
"füllen" : aus Wasserbehälter auffüllen
"leeren" : in Wasserbehälter ausleeren
"umfüllen" : maximal mögliche Menge von einem Krug in den anderen umfüllen
Welche Umfüllungen entsprechen der gezeigten Lösung?
(5,0) G füllen
(2,3) G nach K umfüllen
(2,0) K leeren
(0,2) G nach K umfüllen
(5,2) G füllen
(4,3) G nach K umfüllen
Es wurden also sechs Umfüllschritte benötigt. Hätte man zuerst den kleinen Krug gefüllt, wäre man in acht Schritten zu (4,0) gelangt.
Bevor wir uns mit der mathematischen Systematik des Perelman'schen Papieromputers befassen, soll noch das einleitende Beispiel gelöst werden:
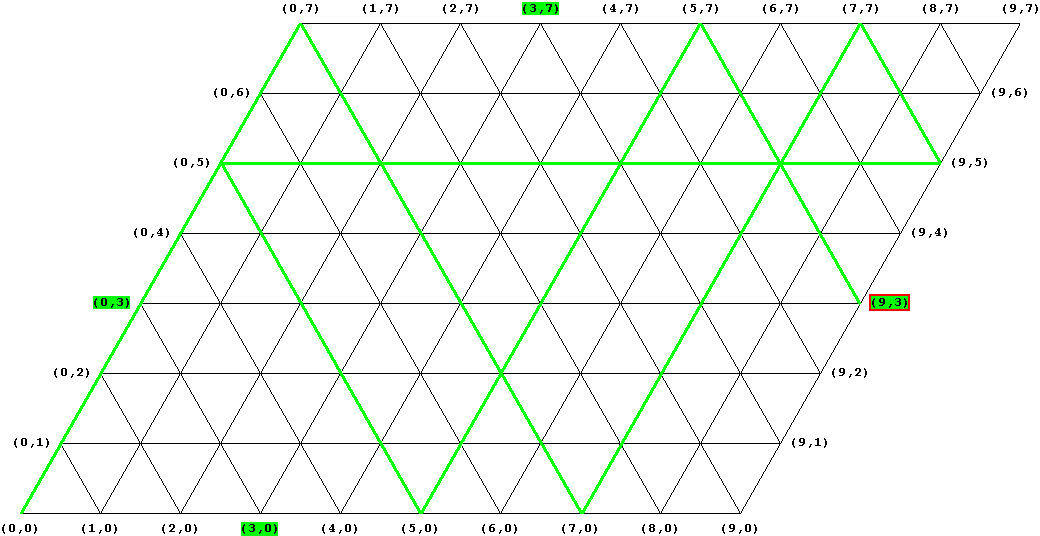
Papiercomputer löst n = 9, m = 7, k = 3
Nun wissen wir, wie der Perelman'sche Papiercomputer funktioniert. Man markiert die Randpunkte mit a = k oder b = k (im Bild grün unterlegt) und probiert die beiden Wege über (0,m) und (n,0) aus - einer davon ist der kürzeste. Wir wollen einige Punkte festhalten, die an der Perelman'schen Idee auffallen:
| (1) |
Die Lösung des Umfüllproblems erfolgt ganz schematisch, "ohne Nachdenken" oder "Probieren".
In den beiden vorgestellten Beispielen werden alle Randpunkte außer (n,m) irgendwann erreicht - und zwar alle genau einmal - , wenn man genügend weit läuft.
Die beiden möglichen Wege ab (0,m) und (n,0) sind identisch, sie verlaufen nur im umgekehrter Richtung.
Die Füllstände (a,b) im Inneren des Parallelogramms werden nicht erreicht und nicht benötigt.
|
Dass der Perelman'sche Papiercomputer so schön funktioniert, soll uns anregen, ihn genauer zu analysieren. Natürlich stellen sich Fragen ein: Ist das Perelman'sche Verfahren für alle n, m, k anwendbar? Ist es das schnellste Verfahren oder sogar das einzige?
Es soll im folgenden n > m > 1 und n > k ≥ 1 gelten, denn mit gleich großen Krügen kann man das Problem offensichtlich nicht lösen, und ein Krug mit 1 Liter Volumen erlaubt trivialerweise die Abmessung von k Litern und wird deshalb nicht zugelassen.
Zum Auftakt wird eine Frage zur Struktur des Papiercomputers gestellt, dann folgt Schritt für Schritt der Beweis zur "Rechtfertigung" des Papiercomputers:
Aufgabe 1
Wenn man den Papiercomputer in ein rechtwinkliges Koordinatensystem transformiert, fällt eine Asymmetrie auf. Wie lässt sich diese erklären? (Gerade diese Asymmetrie erlaubt die regelmäßige "Pflasterung" des Papiercomputers mit gleichseitigen Dreiecken.)
Aufgabe 2
Wie verlaufen die beiden ersten Umfüllschritte sinnvollerweise? Vergleichen Sie dies mit dem Papiercomputer.
Wann endet das Verfahren? (Vorsicht: Wir wissen (bisher) noch nicht, ob a = k oder b = k immer erreicht wird.)
Aufgabe 3
Zeigen Sie:
Nach jedem Umfüllschritt ist ein Krug leer oder ein Krug voll. (Vollständige Induktion.)
Ist entweder ein Krug leer oder ein Krug voll, so gibt es genau vier Umfüllmöglichkeiten, aber nur eine davon ist sinnvoll. Als Nebenresultat erhält man: Jede Umfüllaktion lässt sich rückgängig machen.
Beschränkt man sich auf sinnvolle Umfüllungen, so ist nach dem zweiten und vor dem letzten Umfüllen immer entweder ein Krug leer oder ein Krug voll.
Machen Sie sich klar: Dies ist der Beweis, dass der Perelman'sche Papiercomputer das einzig mögliche Umfüllverfahren beschreibt. Insbesondere werden damit der erste und der vierte Punkt von (1) verständlich.
Beschreiben Sie die verschiedenen Umfüllmöglichkeiten formal, indem Sie (a,b) vor und nach dem Umfüllen angeben. Vergleichen Sie dies mit dem Papiercomputer. Formulieren Sie aber auch eine einfache verbale Regel, anhand der man ohne Papiercomputer die sinnvollen Umfüllschritte durchführen kann.
Wir halten einen Moment inne. Was haben wir bis hierhin gezeigt?
| (2) |
Am Anfang entscheidet man sich, ob zuerst der große oder der kleine Krug gefüllt wird, d.h. man startet entweder über (0,m) und (n,0). Danach gibt es jeweils eine eindeutige Folge sinnvoller Umfüllschritte.
Diese Folge wird durch den Papiercomputer abgebildet. Insbesondere führen die sinnvollen Umfüllschritte immer von Rand zu Rand, und zwar nach der Reflexionsregel der Optik.
Falls das Ziel a = k oder b = k erreicht wird, vergleicht man für die Anfangsschritte (0,m) und (n,0) die Anzahl der jeweils erforderlichen Umfüllschritte und erhält so die optimale Lösung.
|
Was fehlt noch? Wir wissen noch nicht, wann das Umfüllproblem überhaupt lösbar ist, d.h. welche n, m, k eine Lösung erlauben. Diese Frage ist völlig unabhängig vom Papiercomputer, aber dieser wird uns helfen, die Antwort zu veranschaulichen. Wir begeben uns jetzt auf das Gebiet der Zahlentheorie.
Aufgabe 4
Sind n und m nicht teilerfremd, so ist das Umfüllproblem nicht für alle k lösbar. Verwenden Sie die Aufgaben 2 und 3 und zeigen Sie damit die Behauptung induktiv.
n und m seien also ab hier teilerfremd. Testläufe mit dem Perelman'schen Papiercomputer legen nahe, dass dann jedes k erreicht wird (siehe den zweiten Punkt in (1)). Genauer: Es gibt, beginnend mit (0,m), genau einen Weg durch den Papiercomputer, endend bei (n,0); dieser Weg trifft jeden Randpunkt außer (0,0) und (n,m) genau einmal. Der andere Weg beginnt bei (n,0), endet bei (0,m) und ist lediglich die Umkehrung des ersten (siehe den dritten Punkt in (1)). Es gibt nun einen kleinen Trick, um sich die Beweisidee zu veranschaulichen. Beginnt man bei (0,m), so beschreibt der Lösungsweg im Papiercomputer eine Zickzacklinie, bis er auf den rechten Rand trifft. Da er dann zum linken Rand überspringt, liegt es nahe, für den weiteren Lösungsweg den Papiercomputer rechts als Kopie anzulegen; dann entfällt der "Übersprung" von rechts nach links und der Lösungsweg bildet eine duchgehende Zickzacklinie. Man legt soviele Kopien rechts an, bis der Punkt (n,0) erreicht ist. Das soll für n = 5 und m = 3 veranschaulicht werden:

Die roten Linien in diesem Bild sind die "Nahtlinien". Der Schnittpunkt der grünen mit der roten Linie steht für den Umfüllvorgang (n,b) --> (0,b) .
Der Papiercomputer lässt in dieser Darstellung die Umfüllschritte klarer erkennen. Insbesondere wird sichtbar, dass die von der grünen Linie erreichten Punkte am oberen und am unteren Rand immer den Abstand m haben. Machen Sie sich das auch für andere Werte von n und m klar. Dies führt uns unmittelbar zu den nächsten Beweisschritten:
Aufgabe 5
Die bei den sukzessiven Umfüllschritten - beginnend bei (0,m) - erreichten Werte a in (a,0) und (a,m) - also die Füllmengen des großen Kruges, wenn der kleine Krug voll oder leer ist - sind zunächst die Vielfachen von m (verwenden Sie Aufgabe 3). Nach welcher Gesetzmäßigkeit geht es weiter, wenn dabei n überschritten wird? Tipp: Am einfachsten lässt sich dies mit der Modulo-Funktion ausdrücken.
Aufgabe 6
Mit der Folge der Füllmengen a aus Aufgabe 5 ist nun zu zeigen, dass auf dem Weg von (0,m) nach (n,0) alle Punkte am oberen und am unteren Rand des Papiercomputers genau einmal erreicht werden, mit Ausnahme von (0,0) und (n,m). Damit ist dann bewiesen, dass alle (a,0) für 0 < a ≤ n und alle (a,m) für 0 ≤ a < n genau einmal erreicht werden.
Aufgabe 7
Aus Aufgabe 6 lässt sich leicht ermitteln, wieviele Kopien des Papiercomputers nebeneinander gelegt werden müssen, bis man das Ziel (n,0) erreicht hat. Damit können Sie zeigen: Auch alle Punkte am linken und am rechten Rand des Papiercomputers werden genau einmal erreicht, außer (0,0) und (n,m). Damit ist dann bewiesen, dass alle (0,b) für 0 < b ≤ m und alle (n,b) für 0 ≤ b < m genau einmal erreicht werden. Man kann auch hier die Folge der erreichten Randpunkte mit Hilfe der Modulo-Funktion beschreiben und dann zusammenfassend die Abfolge der erreichten Füllstände beschreiben. - Zusammen mit Aufgabe 6 lässt sich jetzt noch zeigen: Für jedes k < n mit k ≠ m gibt es 2 oder 4 zugehörige Randpunkte.
Aufgabe 8
Die beiden Folgen der Umfüllschritte - beginnend bei (0,m) bzw. (n,0) - sind lediglich in der Reihenfolge gespiegelt.
Aufgabe 9
Welche k werden erreicht, wenn n und m nicht teilerfremd sind?
Wir fassen zusammen:
| (3) |
Es lässt sich genau dann jede Menge k ≤ n abmessen, wenn n und m teilerfremd sind. Die Folge der Umfüllschritte lässt sich mit einer einfachen Merkregel beschreiben; das Verfahren dafür ist mit dem Papiercomputer automatisierbar.
Ist k gegeben, so gibt es 2 oder 4 zugehörige Randpunkte des Papiercomputers und einen kürzesten Weg.
|
Damit ist die Aufgabenstellung umfassend gelöst und die Idee von Y. I. Perelman gebührend gewürdigt.
Man sollte sich aber noch mit dem Fall befassen, dass in der Formulierung des Problems nicht ein Reservoir unbekannten Inhalts, sondern ein weiterer Krug mit Volumen r ≥ n vorkommt, der anfangs gefüllt ist. In vielen Aufgaben hat dieser Krug das Volumen r = n + m ; z.B. ist das Beispiel mit Krügen von 3, 5 und 8 Litern Volumen sehr gängig. Manchmal sieht man auch r > n + m . Diese beiden Fälle lassen sich bequem zusammenfassen, denn die bisher durchgeführten Beweisschritte lassen sich ohne weiteres auf r ≥ n + m anwenden, wenn man den größten Krug wie den Wasserbehälter behandelt. Allerdings lässt sich dann der Papiercomputer sinnvoll ergänzen: Neben jeden Randpunkt kann man den zugehörigen Füllungsstand des größten Kruges notieren und hat damit zusätzliche Möglichkeiten, k zu erreichen; insbesondere können sich dadurch kürzere Lösungswege ergeben. Außerdem kommen dann natürlich auch Werte k > n in Frage. In den nächsten beiden Aufgaben seien wieder n und m teilerfremd.
Aufgabe 10
Geben Sie je ein Beispiel für r = n + m und r > n + m an, in denen am Ende die abzumessende Menge k im größten Krug ist und man weniger Umfüllschritte benötigt als mit dem Verfahren aus (2). Man wird von Hand, d.h. mit dem Papiercomputer, recht schnell bei kleinen n, m fündig.
Aufgabe 11
Welche Mengen k kann man abmessen, wenn r ≥ n + m ist? In welchen Fällen kann man alle k ≤ r abmessen?
Der Fall r > n + m weist noch eine weitere interessante Facette auf: Das Ergebnis aus Aufgabe 9 stimmt hier nicht. Man kann in Einzelfällen bei nicht teilerfremden n und m Füllmengen k abmessen, die bei einem Reservoir unbekannten Inhalts nicht erreicht werden können.
Aufgabe 12
Sei r > n + m mit nicht teilerfremden n und m .
Geben Sie ein Beispiel an, in dem jede Menge k ≤ n abgemessen werden kann.
Für welche n, m, r geht das im allgemeinen?
Warum kann man nie alle k ≤ r abmessen?
Und zum Schluss: Was ist mit r < n + m ? In diesem Falle wird der Papiercomputer an seiner oberen rechten Ecke "amputiert". Für n = 5, m = 3, r = 6 sieht das so aus:
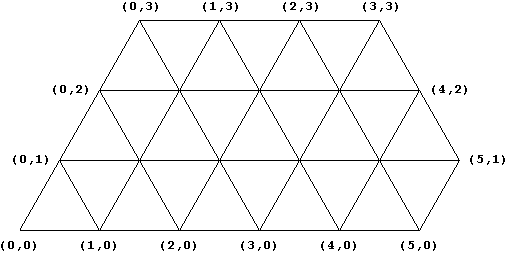
In diesem Beispiel lassen sich alle k erreichen. Aber gilt das immer?
r = n + m - 1 bedeutet keine Einschränkung; alle k ≤ r können abgemessen werden, denn es fehlt am Papiercomputer ja nur der Punkt (n,m), von dem wir gesehen haben, dass man ihn nicht benötigt.
Leider gilt das im Allgemeinen nicht für kleinere r . Man kann das ausprobieren, indem man in unserem Eingangsbeispiel mit n = 9 und m = 7 einen dritten Krug mit Volumen r = 12 einführt und versucht, die Menge k = 6 abzumessen.
Lösung
Publiziert 2008-09-07 Stand 2007-09-07
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite
 Y. I. Perelman
Y. I. Perelman





