Wie Meister Roriczer Sieben- und Achtecke konstruierte.

          Die Lösung steht im unteren Teil der Seite.

Der Regensburger Dombaumeister Matthäus Roriczer (ca. 1430 - ca. 1495) hat das Büchlein  Geometria deutsch  geschrieben. In ihm sind die Lösungen mehrerer elementarer geometrischer Probleme enthalten, die wichtig für den Kirchenbau sind. Dabei kommt es Roriczer vor allem auf möglichst elegante Konstruktionsvorschriften an, die von den Architekten und Handwerkern an den Dombauhütten mit einfachen Mitteln umgesetzt werden konnten. Regelmäßige Vielecke wurden u.a. beim Bau von Kirchenfenstern benötigt. Zwei schöne Konstruktionen solcher Polygone wollen wir uns anschauen.


Konstruktion eines regelmäßigen Achtecks in ein vorgegebenes Quadrat

Das Achteck soll nicht mit vier Ecken die Quadratseiten berühren, sondern vier seiner Seiten sollen mittig auf den Quadratseiten liegen, so wie in Bild 1a:



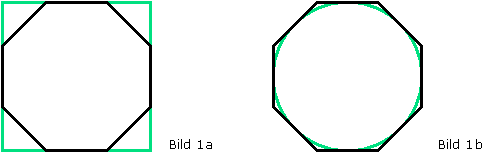
Wenn man ausrechnet, wo die Eckpunkte des Achtecks liegen, weiß man auch, wie Meister Roriczer mit einer einzigen und sehr einfachen Zirkeleinstellung diese Punkte einzeichnen konnte. Wer eine Hilfe braucht, kann den Originaltext lesen, der aber in altem und etwas schwer verständlichem Deutsch verfasst ist (in der Lösung wird eine Übersetzung gegeben).

         Wie hat Meister Roriczer das regelmäßige Achteck konstruiert ?
         Warum ist die Konstruktion des Achtecks in ein Quadrat äquivalent zur Konstruktion um einen Kreis (siehe Bild 1b) ?


Konstruktion eines regelmäßigen Siebenecks in einen vorgegebenen Kreis

Wer ein wenig über die Konstruktion regelmäßiger Polygone weiß, wird an dieser Stelle stutzig. Denn man kann beweisen, dass die Konstruktion des regelmäßigen Siebenecks (Bild 2a) mit Zirkel und Lineal unmöglich ist. (Mehr Informationen dazu findet man auf der Briefmarkenseite über Carl Friedrich Gauß.)  Matthäus Roriczer gibt aber in der  Geometria deutsch  eine einfache und schöne Konstruktion an. Man kann sie sich im Originaltext anschauen (in der Lösung wird eine Übersetzung gegeben), aber vermutlich reicht schon ein Blick auf seine Zeichnung (siehe Bild 2b):



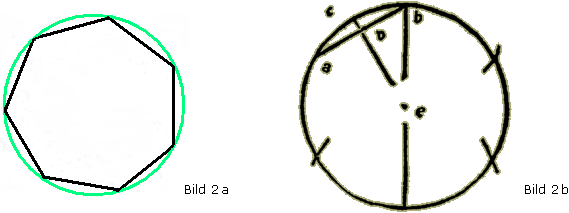
         Wie hat Meister Roriczer das (fast) regelmäßige Siebeneck konstruiert ?
         Wie genau ist diese Näherungslösung ?
         Warum ist für alle regelmäßigen n-Ecke die Konstruktion in einen Kreis äquivalent zur Konstruktion um einen Kreis ?
         (Dies erweitert auch die Äquivalenzaufgabe aus dem Abschnitt über das Achteck oben.)

Lösung

       Wie hat Meister Roriczer das regelmäßige Achteck konstruiert ?

Das Quadrat in Bild 3 soll die Seitenlänge  a  haben, das Achteck die (noch unbekannte) Seitenlänge  b . Will man die Eckpunkte des Achtecks einzeichnen, so wird man wohl zunächst deren Abstände von den Quadratecken berechnen und mit Hilfe von  a  ausdrücken.



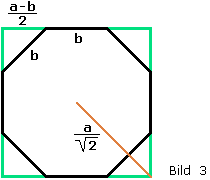
Wir schauen uns die linke obere Ecke des Quadrates an. Der Abstand zu den nächsten Eckpunkten des Achtecks beträgt  (a - b)/2 . Nach Pythagoras ist dann  b² = (a - b)²/2 . Wurzelziehen macht aus dieser Gleichung:



Damit ist man schon am Ziel. Denn die letzte Formel ist besonders einfach. Sie besagt, dass die Abstände der Quadratecken zu den jeweils übernächsten Ecken des Achtecks  a/2^1/2  beträgt. Dies ist aber gerade die Länge einer halben Diagonalen des Quadrats (siehe Bild 3).

Lösung: Man zeichnet beide Diagonalen des Quadrats und erhält so den Mittelpunkt. Nimmt man dann eine halbe Diagonale in den Zirkel, kann man alle Ecken des Achtecks abtragen.

Nun wird auch Roriczers Originaltext verständlich, den man hier übersetzt findet.



       Warum ist die Konstruktion des Achtecks in ein Quadrat äquivalent zur Konstruktion um einen Kreis ?

Konstruktion des Innenachtecks in einem Quadrat bekannt, Umachteck eines Kreises gesucht:
Man zeichnet das Umquadrat zum Kreis. Dessen Innenachteck ist gleich dem Umachteck des Kreises.

Konstruktion des Umachtecks eines Kreises bekannt, Innenachteck in einem Quadrat gesucht:
Man zeichnet den Inkreis des Quadrates. Dessen Umachteck ist gleich dem Innenachteck des Quadrates.



       Wie hat Meister Roriczer das (fast) regelmäßige Siebeneck konstruiert ?

Wie lang ist die Sehne, die Meister Roriczer in den Kreis gezeichnet hat (siehe Bild 2b) ? Man misst nach und erkennt, dass es sich um den Kreisradius handelt. Also ist die Sehne nicht die gesuchte Seite des Siebenecks, sondern die des regelmäßigen Sechsecks. In der Skizze stellt sie eine Hilfslinie dar. Die Mittelsenkrechte trifft den Mittelpunkt des Kreises. Offenbar kommt Roriczer mit diesen Hilfslinien aus. Die einzige Strecke, die für die Seite des Siebenecks in Frage kommt, ist offenbar  d-e , also der Abstand der Sehne vom Kreismittelpunkt. Das kann man ausprobieren: Nimmt man diese Strecke in den Zirkel und trägt sie wiederholt auf dem Kreis ab, so erhält man tatsächlich ein Siebeneck. Wir wissen natürlich, dass die Konstruktion nicht völlig exakt sein kann, aber beim Zeichnen merkt man das nicht.

Lösung: Man zeichnet eine Sehne mit der Länge des Radius und verbindet ihre Mitte mit dem Kreismittelpunkt. Diese Verbindungsstrecke nimmt man als Seite des Siebenecks. Die Seiten des Siebenecks sind also gleich dem Inkreisradius des Innensechsecks.

Nun wird auch Roriczers Originaltext verständlich, den man hier übersetzt findet.  -  Da es sich nur um ein Näherungsverfahren handelt, findet man diese Konstruktion nur in wenigen Geometriebüchern. Sie war schon in der Antike bekannt und wurde durch Heron von Alexandria beschrieben.



       Wie genau ist diese Näherungslösung ?

Der Einfachheit halber sei der Kreisradius gleich  1 . Halbiert man eine Seite des regelmäßigen Innensiebenecks, so entsteht ein rechtwinkliges Dreieck mit dem Radius als Hypothenuse und dem Zentrumswinkel  360°/14 . Dann hat die halbe Siebeneckseite die Länge  sin 360°/14 ; für die ganze Siebeneckseite ergibt das gerundet die Länge  0.8677675 . Die Konstruktion von Heron und Roriczer dagegen ergibt (siehe Bild 2b) die Seitenlänge  3^1/2/2 , also gerundet  0.8660254 . Das entspricht einer Abweichung von nur etwa  0.2%  und ist damit für praktische Anwendungen genau genug.



       Warum ist für alle regelmäßigen n-Ecke die Konstruktion in einen Kreis äquivalent zur Konstruktion um einen Kreis ?
       (Dies erweitert auch die Äquivalenzaufgabe aus dem Abschnitt über das Achteck oben.)

Liegt das Innenpolygon vor, so kann man an allen Ecken Tangenten an den Kreis einzeichnen. Die Schnittpunkte dieser Tangenten für benachbarte Ecken sind dann die Ecken des Außenpolygons. Das ist aber eine etwas mühsame Methode. Es reichen bereits zwei (benachbarte) Tangenten: In Bild 4 sind  a  und  b  benachbarte Ecken des Innenpolygons. Die zugehörigen Tangenten schneiden sich in  c . Also verläuft durch  c  der Umkreis des gesuchten Polygons. Mit den Schnittpunkten  d  und  e  hat man dann schon zwei Polygonseiten und kann deren Länge auf dem Umkreis rundum abtragen.



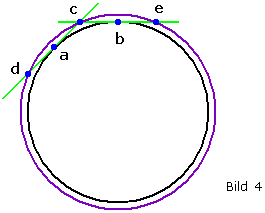
Liegt das Außenpolygon vor, verbindet man einfach die Berührpunkte (des Außenpolygons mit dem Kreis) und erhält so das Innenpolygon.



Ein weiteres geometrisches Problem steht bei der Briefmarke # 65.

Publiziert 2008-12-29          Stand 2008-04-20

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem