Die Kernfrage dieses Problems lautet:
Wie kann man das Würfeln (mit einem gewöhnlichen 6-seitigen Würfel) durch eine Folge von Münzwürfen möglichst effizient ersetzen?
Über diese Frage kann man nachdenken, ohne die folgenden Ausführungen gelesen zu haben. Wer jedoch erst die Details kennenlernen möchte, die in der Kernfrage stecken, sollte weiterlesen.
Durch wiederholtes Werfen einer Münze kann man zufällige Folgen von 0 und 1 erzeugen. Durch Werfen eines Würfels erhält man zufällige Folgen von Zahlen aus {1,2,3,4,5,6}. Wenn man einen Würfel braucht, aber keinen hat, kann man die Augenzahlen durch 3 Münzwürfe erzeugen, z.B. so:
000 → 1
001 → 2
010 → 3
011 → 4
100 → 5
101 → 6
110 → nochmal 3 Münzwürfe
111 → nochmal 3 Münzwürfe
Man braucht also im Durchschnitt mehr als 3 Münzwürfe, da man von den 8 möglichen Wurffolgen nur 6 verwenden kann. Das ist eine ungünstige Situation, die für bestimmte anders geformte "Würfel" nicht gilt. Hat der "Würfel" z.B. 4 Seiten (Tetraeder), benötigt man 2 Münzwürfe, bei einem 8-seitigen "Würfel" (Oktaeder) benötigt man 3 Münzwürfe, allgemein bei einem 2n-seitigen "Würfel" n Münzwürfe. Im Prinzip lassen sich alle s-seitigen "Würfel" mit s ≥ 2 herstellen ( s = 2 → Münze; s ∈ {4,6,8,12,20} → platonische Körper; sonst prismenförmige Kreisel, siehe Bild).
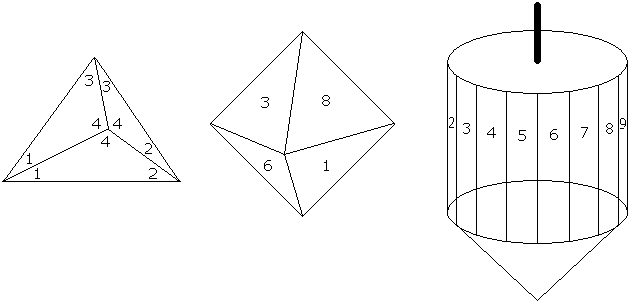
"Würfel" mit s = 4, s = 8, s = 16 Seiten
Somit braucht man zur Erzeugung der Augenzahlen eines gewöhnlichen Würfels mehr Münzwürfe als bei einem 8-seitigen Würfel. Offenbar benötigt man das Minimum von log2 s Münzwürfen für s Würfelseiten genau dann, wenn s eine Zweierpotenz ist.
Ab hier wollen wir uns nur noch mit gewöhnlichen Würfeln mit 6 Seiten beschäftigen.
Aufgabe 1
Wie viele Münzwürfe braucht man im Durchschnitt, wenn man eine Münze in 3er-Folgen solange wirft, bis man eine Augenzahl zwischen 1 und 6 erzeugt hat?
Wir haben oben gesehen, dass 110 und 111 nicht brauchbar sind und zu erneutem Werfen der Münze führen. Aber das weiß man schon nach den beiden ersten Münzwürfen 11x , so dass man danach abbrechen und eine neue Serie starten kann. Also könnten z.B. die ersten drei erzeugten Augenzahlen 2, 4, 1 so zustande kommen:
11 001 → 2
011 → 4
11 11 000 → 1
Hier hätte man also für 3 Augenzahlen 15 Münzwürfe benötigt; ohne Abbruch wären es 18 gewesen.
Aufgabe 2
Wie viele Münzwürfe braucht man im Durchschnitt zur Erzeugung einer Augenzahl zwischen 1 und 6 , wenn man bei den nicht brauchbaren Würfen rechtzeitig abbricht?
Mit oder ohne Abbruch: Im Vergleich zum 8-seitigen "Würfel" (oder anderen 2n-seitigen "Würfeln") ist der Münzwurf als Ersatz zum normalen Würfeln umständlich. Für s = 2n sind lediglich log2 s Münzwürfe erforderlich; dieser Wert würde theoretisch für s = 6 nur log2 6 ≈ 2,58496 betragen - tatsächlich braucht man deutlich mehr als 3 Münzwürfe, wie die Fragen 1 und 2 gezeigt haben.
Es gibt aber eine Möglichkeit, näher an den theoretischen Wert log2 6 heranzukommen - sogar beliebig nahe. In der Regel wird man ja mehrere (oder viele) Augenzahlen erzeugen wollen, etwa für ein Gesellschaftsspiel. Dann möchte man also eine lange Folge von Augenzahlen zwischen 1 und 6 durch eine Folge von 0 und 1 darstellen. Nun kommt die gute Idee, wie man dies möglichst effektiv durchführt: Man erzeugt die Augenzahlen nicht einzeln (also durch jeweils 3 Münzwürfe), sondern man verkettet die Folge der Münzwürfe zu einer langen Binärzahl. Diese wird dann insgesamt (d.h. nicht abschnittsweise) transformiert in ebenfalls verkettete Augenzahlen. Also liegt es nahe, statt der Augenzahlen 1 bis 6 die Zahlen 0 bis 5 zu nehmen, um in der Basis 6 rechnen zu können, also in Hexalzahlen. Um es kurz zusammenzufassen:
Man rechnet eine Zahl zur Basis 2 in eine Zahl zur Basis 6 um. Die erste entspricht einer Folge von Münzwürfen, die zweite einer Folge von Augenzahlen beim Würfel.
Beispiel: Wir werfen 13-mal die Münze und erhalten damit die Binärzahl 00001011001102 . Transformation in die Hexalzahl ergibt: 00001011001102 = 013546 (entspricht den Augenzahlen 1, 2, 4, 6, 5 ). Die führende 0 in der Hexalzahl ist wichtig, denn wir erhalten mit diesem Verfahren immer genau 5 Augenzahlen: Mit 13 Münzwürfen kann man 213 = 8192 Zufallszahlen im Bereich 00000000000002 bis 11111111111112 erzeugen. Wegen 11111111111112 = 1015316 decken also die binären Zufallszahlen alle 5-stelligen Hexalzahlen 000006 bis 555556 ab. Die Binärzahlen 11110011000002 bis 11111111111112 können nicht verwertet werden, sie entsprechen nämlich den (sechsstelligen) Hexalzahlen von 1000006 bis 1015316 . Wir werden noch sehen, dass wir damit dem theoretischen Minimalwert für das Verhältnis Münzwürfe/Augenzahlen schon erheblich nähergekommen sind.
Im Folgenden soll m die Anzahl der Augenzahlen beim Würfeln sein, die man erzeugen möchte; n = n(m) sei die dafür erforderliche Anzahl von Münzwürfen.
Aufgabe 3
Berechnen Sie n aus m .
Setzen Sie am = n/m . Berechnen Sie das theoretische Minimum a der am .
Aufgabe 4
Es sind nicht alle erzeugten binären Zufallszahlen verwertbar. Analog zu Aufgabe 1 stellt sich also die Frage:
Wie viele Münzwürfe d1 braucht man im Durchschnitt, wenn man eine Münze in Folgen der Länge n solange wirft, bis man eine Hexalzahl der Länge m erzeugt hat?
Dafür ist es wie bei den Aufgaben 1 und 2 hilfreich, die Wahrscheinlichkeit p für die zufällige Erzeugung einer n-stelligen Binärzahl zu berechnen, die einer m-stelligen Hexalzahl entspricht.
Auch hier kann man bei den nicht verwendeten binären Zufallszahlen vorzeitig abbrechen. Man berechnet die größte verwertbare Binärzahl v (diese entspricht 55...56 ). Dann wirft man wiederholt die Münze für die binäre Zufallszahl, beginnend bei der vordersten Stelle (also bei der höchsten 2er- Potenz). Abbruch erfolgt, sobald eine Ziffer der Zufallszahl größer als die entsprechende Ziffer in v ist.
Aufgabe 5
Analog zu Aufgabe 2 stellt sich also die Frage: Wie viele Münzwürfe d2 braucht man im Durchschnitt zur Erzeugung einer Hexalzahl der Länge m , wenn man bei den nicht brauchbaren Würfen rechtzeitig abbricht?
Welche Werte von m sind besonders günstig? Das sind offenbar diejenigen, bei denen von den 2n möglichen Wurffolgen nur wenige unbrauchbar sind. Also sucht man m mit 6m ≈ 2n (dabei ist 6m ≤ 2n wegen der Wahl von n gewährleistet).
Aufgabe 6
Machen Sie eine Tabelle für 1 ≤ m ≤ 50 , die folgende Werte enthält:
- m
- n (siehe Aufgabe 3)
- p (Anteil der brauchbaren binären Zufallszahlen)
- d1 (durchschnittliche Anzahl insgesamt benötigter Münzwürfe bei nicht-abbrechendem Verfahren, siehe Aufgabe 4)
- v1 = (d1/m)/a (Verhältnis der durchschnittlichen Anzahl benötigter Münzwürfe für einzelne Augenzahlen zum theoretischen Minimum bei nicht-abbrechendem Verfahren)
- d2 (durchschnittliche Anzahl insgesamt benötigter Münzwürfe bei abbrechendem Verfahren, siehe Aufgabe 5)
- v2 = (d2/m)/a (Verhältnis der durchschnittlichen Anzahl benötigter Münzwürfe für einzelne Augenzahlen zum theoretischen Minimum bei abbrechendem Verfahren)
Berechnen Sie überschlägig (d.h. in ungefährer Näherung) für große n , was sich für die di und die vi in den extremen Fällen p ≈ 1 bzw. p ≈ 0,5 ergibt. Insbesondere ist dabei das folgende Ergebnis interessant:
p ≈ 0,5 ⇒ d2 ≈ n + 3
Die Tabelle zeigt große Unterschiede in der Effizienz der Münzwürfe für die Erzeugung von Würfel-Augenzahlen. Einen einzigen Würfelwurf oder zwei solche Würfe durch Münzwürfe zu ersetzen, erfordert einen unverhältnismäßig großen Aufwand. Aber m = 5 oder m = 41 erbringen sehr gute Ergebnisse mit d1/m und d2/m nahe bei a . Ist das Zufall oder gibt es eine Gesetzmäßigkeit für die "guten" m ? Dafür gibt es einen Ansatz:
Es gilt n ≈ a·m ( a kommt in der Lösung von Aufgabe 3 vor). Aussichtsreiche Kandidaten für m , die ein effizientes Verfahren erlauben, kann man also durch Näherungsbrüche b/c ≈ a finden; dann kann man m = c wählen und somit n = b .
Damit kommen wir zur abschließenden Aufgabe. Der Faktor a aus Aufgabe 3 soll in hoher Genauigkeit als Bruch approximiert werden. Dafür gibt es das Verfahren der Kettenbrüche. Man benutzt am besten ein Programm, das die Kettenbruch-Folge bi/ci ≈ a berechnet. Die Theorie der Kettenbrüche stellt sicher, dass lim i→∞ bi/ci = a . Dabei sind die bi/ci abwechselnd > a und < a .
Aufgabe 7
Bestimmen Sie mit Hilfe der Kettenbruchentwicklung, welche m sich besonders gut für eine effiziente Ersetzung von Hexalzahlen durch Binärzahlen eignen.
Lösung
Kategorie: Zahlen und Zahlsysteme, Berechnung von π