Chinesisches Nim - Wijthoffs Spiel
Die Lösung steht im unteren Teil der Seite.
Dies ist bereits das dritte Nim-Problem auf dieser Website (siehe # 46 und # 58). Es ist benannt nach
Willem Abraham Wijthoff (1865 - 1939), einem niederländischen Mathematiker, der es 1907 beschrieben hat. Sehr häufig findet man es unter dem Namen Chinesisches Nim.
Robert Heidenreich hat dieses Spiel in seiner Bachelor-Thesis (2011) an der Technischen Hochschule Mittelhessen analysiert.
Hier ist die Spielregel: Zwei Spieler nehmen abwechselnd Münzen von zwei Stapeln weg. Die beiden Münzstapel enthalten bei Spielbeginn verschiedene Anzahlen a und b von Münzen. Der Spieler, der am Zuge ist, sucht sich entweder einen Stapel aus und entnimmt ihm beliebig viele Münzen, oder er nimmt von beiden Stapeln dieselbe Anzahl Münzen weg. Sieger des Spiels ist, wer die letzte Münze nimmt.
Wie auch andere Nim-Spiele ist Chinesisches Nim im Sinne der Spieltheorie ein neutrales oder objektives Spiel. Für jede Spielposition (a,b) gewinnt bei fehlerlosem Spiel entweder immer der Anziehende oder der Nachziehende.
Als Gewinnposition soll (a,b) gelten, wenn der Anziehende gewinnt; (a,b) heißt Verlustposition, wenn der Nachziehende gewinnt. Offenbar liegt bei a = 0 , bei b = 0 und bei a = b eine Gewinnposition vor. Eine Spielanalyse für kleine Werte von a und b zeigt schnell, dass es viel mehr Gewinn- als Verlustpositionen gibt. Es liegt also nahe, nur die Verlustpositionen zu bestimmen. Da es sich um abzählbar viele Positionen handelt, sollen sie übersichtlich angeordnet werden. Zunächst kann man immer a < b wählen. Die Werte von a für die Verlustpositionen sollen aufsteigend geordnet werden, wir wollen sie mit xn bezeichnen. Die zugehörigen Werte von b nennen wir dann yn .
- Verlustpositionen: (xn , yn) mit xn monoton wachsend und xn < yn
Aufgabe 1
Zeigen Sie: Alle Zahlen in den Paaren (xn , yn) kommen nur einmal vor, d.h. xi ≠ xk , yi ≠ yk , xi ≠ yk für i ≠ k .
Von Hand oder mit einem kleinen Programm können Sie die ersten Folgenglieder (xn , yn) berechnen:
- (1, 2), (3, 5), (4, 7), (6, 10), (8, 13), (9, 15), (11, 18), (12, 20), (14, 23), ...
Erkennen Sie das Bildungsgesetz für diese Folge? Bei den xn muss man vielleicht etwas länger hinschauen, aber lesen Sie erst mal nicht weiter und versuchen Sie es selbst. Die Regel für yn erkennt man dann viel leichter.
Hier ist ein Tipp für die xn : xn+1 ergibt sich aus dieser Vereinigungsmenge :
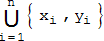
Aufgabe 2
Geben Sie eine rekursive Definition für die (xn , yn) an. Der Beweis kann mit vollständiger Induktion erfolgen.
Aufgabe 3
Folgerungen:
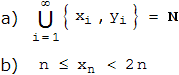
Mit einer Liste der (xn , yn) haben wir aber noch keine wirklich gute Strategie, um dieses Spiel zu gewinnen. Deshalb wollen wir der Frage nachgehen, ob es eine geschlossene Formel für (xn , yn) gibt. Es gibt sie tatsächlich, und sie ist recht einfach, aber nicht ganz leicht zu erkennen. Ausgangspunkt ist die Aufgabe 3 b). Offenbar ist xn = q·n mit q ∈ [1, 2) . Aber q wird natürlich von n abhängen. Also bildet man q = xn/n , um Genaueres über q herauszufinden (dafür braucht man natürlich eine längere Liste der xn ; das geht zur Not noch von Hand, aber ein kleines Programm für die Rekursion aus Aufgabe 2 erspart Arbeit).
Aufgabe 4
Es gilt xn/n  r , und r ist eine gut bekannte irrationale Zahl.
Genauer: lim xn/n = r und xn/n < r .
Geben Sie eine Vermutung ab, welche Zahl r ist.
r , und r ist eine gut bekannte irrationale Zahl.
Genauer: lim xn/n = r und xn/n < r .
Geben Sie eine Vermutung ab, welche Zahl r ist.
Setzt man also näherungsweise xn  r·n , so ist immer xn < r·n , aber nur mit einer geringen Differenz. Da xn ganzzahlig ist, r·n aber nicht, stellt sich nun die Vermutung über die geschlossene Formel ein:
r·n , so ist immer xn < r·n , aber nur mit einer geringen Differenz. Da xn ganzzahlig ist, r·n aber nicht, stellt sich nun die Vermutung über die geschlossene Formel ein:
Aufgabe 5
Stellen Sie (xn , yn) in geschlossener Form dar (erst mal ohne Beweis).
Natürlich lässt sich diese geschlossene Formel für die Verlustpositionen auch beweisen, aber es ist nicht ganz einfach, auf die richtige Beweisidee zu kommen. Deshalb gehört der Beweis nicht zur Aufgabenstellung. Wer ihn führen möchte und ein wenig Hilfe braucht, kann den Hinweis lesen.
Nun kommen wir zur Strategie für dieses Spiel. Was sollte der anziehende Spieler tun, wenn er die Spielposition (a,b) vorfindet? Zunächst wird er überprüfen, ob (a,b) = (xn , yn) ist. In diesem Falle ist er auf der Verliererstraße (wenn sein Gegner keinen Fehler macht). Ansonsten muss er Münzen von einem Stapel oder von beiden Stapeln so wegnehmen, dass er eine Verlustposition für seinen Gegner hinterlässt.
Aufgabe 6
Was ist die richtige Strategie für
- a = xn und b > yn ,
- a = xn und b < yn ,
- a = yn ?
Aufgabe 7
Für die Strategie in Aufgabe 6 ist es nützlich, a = xn bzw. a = yn möglichst leicht überprüfen zu können. Wie kann man das machen?
Aufgabe 8
Ein Beispiel: Wie verhalten Sie sich, wenn Sie bei (1995, 2010) am Zuge sind?
Lösung
Aufgabe 1
Wenn man annimmt, dass z in zwei Verlustpositionen vorkommt ( a = z oder b = z ), muss es mit "Partnern" c und d kombiniert sein; o.E. sei c < d . Wenn der Anziehende (z,d) oder (d,z) vorfindet, kann er vom d-Stapel d - c Münzen wegnehmen, also c Münzen hinterlassen und somit eine Verlustposition erzeugen. Dann wäre aber die Ausgangsposition eine Gewinnposition gewesen. Somit ist die Annahme falsch.
Aufgabe 2
Der Schlüssel für die rekursive Berechnung von xn+1 mittels der (xi,yi) (i ≤ n) liegt in dieser Menge:
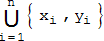
Wir wählen beispielhaft n = 4,6,9 und schauen uns jeweils die Vereinigungsmenge sowie xn+1 an:

Vermutung: xn+1 ist die kleinste natürliche Zahl, die nicht unter den xi oder yi mit i ≤ n vorkommt. Formal heißt das:
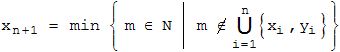
Die Vermutung über die yn ergibt sich durch bloßes Hinsehen:
yn = xn + n
Beweis
(x1,y1) = (1,2) und (x2,y2) = (3,5) berechnet man leicht von Hand. Das ist der Induktionsanfang. Sei nun n > 1 und seien die (xi,yi) für i ≤ n wie in der Vermutung gebildet. Wegen Aufgabe 1 ist dann das kleinstmögliche a , das für xn+1 in Frage kommt:
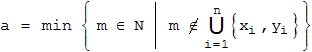
Wir zeigen nun, dass mit xn+1 = a und yn+1 = xn+1 + n+1 eine Verlustposition entsteht.
Nimmt man vom kleineren Stapel oder von beiden Stapeln Münzen weg, so bleibt die Differenz größer als n ; also kann kein (xi,yi) für i ≤ n entstehen, aber auch kein (xi,yi) für i > n+1 , da die xi streng monoton wachsen.
Nimmt man vom größeren Stapel Münzen weg, so entsteht die Differenz d ≤ n . Dafür käme als Verlustposition nur (xd,yd) in Frage. Der Stapel mit xn+1 Münzen wurde nicht verändert, aber xn+1 ≠ xd und xn+1 ≠ yd wegen der Definition von xn+1 .
In beiden Fällen hinterlässt man also eine Gewinnposition; deshalb muss die Ausgangsposition eine Verlustposition sein. Wegen der Monotonie der xn ist also xn+1 = a korrekt gewählt. Ein weiteres yn+1 außer yn+1 = xn+1 + n+1 kann es wegen Aufgabe 1 nicht geben.
Aufgabe 3
Die Folgerungen liegen auf der Hand. Denn aus der Lösung zu Aufgabe 2 folgt, dass die Vereinigung aller {xi,yi} für i ≤ n alle natürlichen Zahlen {1, 2, ... , xn} umfasst und wegen n ≤ xn (Monotonie der xn ) mindestens die ersten n natürlichen Zahlen enthält.
Auch xn < 2n folgt induktiv aus dem Beweis von Aufgabe 2: Wäre xn+1 ≥ 2n+2 , so lägen mindestens 2n+1 natürliche Zahlen unterhalb von xn+1 ; aber die Vereinigungsmenge aus der rekursiven Definition von xn+1 enthält nur 2n Elemente.
Aufgaben 4 und 5
Ein wenig Probieren zeigt, dass xn/n immer näher (von unten) an r  1,62 rückt. So stellt sich die Vermutung ein, dass r = Φ ist. Φ steht für die Goldene Zahl:
1,62 rückt. So stellt sich die Vermutung ein, dass r = Φ ist. Φ steht für die Goldene Zahl:
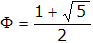
Somit wäre xn  Φ·n mit xn < Φ·n , und es liegt nahe, dass xn =
Φ·n mit xn < Φ·n , und es liegt nahe, dass xn =  Φ·n
Φ·n  . Dabei steht
. Dabei steht  .
.  für die ganzzahlige Abrundung.
für die ganzzahlige Abrundung.
Dann ist yn =  Φ·n
Φ·n  + n =
+ n =  Φ·n + n
Φ·n + n  =
=  ( Φ + 1 )·n
( Φ + 1 )·n  =
=  Φ2·n
Φ2·n  .
.
Beweis
Die letzte Umformung werden wir in Aufgabe 7 verwenden; sie folgt aus der Tatsache, dass Φ eine Lösung von Φ2 - Φ - 1 = 0 ist.
Aufgabe 6
- a = xn und b > yn
Der Anziehende nimmt b - yn Münzen vom größeren Stapel weg und erzeugt so für seinen Gegner die Verlustposition (xn,yn) .
- a = xn und b < yn
Sei d = b - a . Dann ist d < n . Der Anziehende nimmt von beiden Stapeln xn - xd Münzen weg und erzeugt so für seinen Gegner die Verlustposition (xd,yd) .
- a = yn
Der Anziehende nimmt vom größeren Stapel b - xn Münzen weg, lässt damit xn Münzen in diesem Stapel übrig und erzeugt so für seinen Gegner eine Verlustposition.
Aufgabe 7
Wie erkennt man, dass a = xn =  Φ·n
Φ·n  ist?
ist?
 Φ·n
Φ·n  ist eine natürliche Zahl mit
ist eine natürliche Zahl mit  Φ·n
Φ·n  = Φ·n - ε und ε ∈ (0,1). ε = 0 scheidet aus, da Φ·n irrational ist.
= Φ·n - ε und ε ∈ (0,1). ε = 0 scheidet aus, da Φ·n irrational ist.
Zur Abkürzung setzen wir φ = 1/Φ = Φ - 1  0,618 .
0,618 .
a =  Φ·n
Φ·n  ⇔ es ex. ε ∈(0,1) mit a = Φ·n - ε
⇔ es ex. ε ∈(0,1) mit a = Φ·n - ε
⇔ es ex. ε ∈(0,1) mit a/Φ = n - ε/Φ
⇔ a/Φ ∈ (n - 1/Φ, n)
⇔ a·φ ∈ (n - φ, n)  ((n-1)+0,382 , n)
((n-1)+0,382 , n)
Damit kann man die allermeisten a überprüfen. Man bildet das Produkt a·φ ; sind die Nachkommastellen oberhalb von ...,382 , so ist a =  Φ·n
Φ·n  = xn , und n =
= xn , und n =  a·φ
a·φ  + 1 .
+ 1 .
Allerdings könnten die Nachkommastellen von a·φ sehr nah bei ...,382 liegen, so dass man viele Nachkommastellen von n - φ überprüfen muss.
Wir wollen deshalb außer dem Kriterium a·φ ∈ (n - φ, n) noch ein weiteres formulieren, das sich direkt aus der Beweisführung des ersteren ergibt:
a =  Φ·n
Φ·n  ⇔
⇔ 
 a/Φ
a/Φ  · Φ
· Φ  = a und n =
= a und n =  a/Φ
a/Φ 
(  .
.  steht für die ganzzahlige Aufrundung.)
steht für die ganzzahlige Aufrundung.)
Ganz analog prüft man, ob a = yn =  Φ2·n
Φ2·n  ist:
ist:
a =  Φ2·n
Φ2·n  ⇔ a/Φ2 ∈ (n - 1/Φ2, n) = ((n-1) + φ, n)
⇔ a/Φ2 ∈ (n - 1/Φ2, n) = ((n-1) + φ, n)  ((n-1) + 0,618, n)
((n-1) + 0,618, n)
oder
a =  Φ2·n
Φ2·n  ⇔
⇔ 
 a/Φ2
a/Φ2  · Φ2
· Φ2  = a und n =
= a und n =  a/Φ2
a/Φ2 
Aufgabe 8
1995·φ  1232,978 ⇒ x1233 = 1995 ⇒ y1233 = 3228
1232,978 ⇒ x1233 = 1995 ⇒ y1233 = 3228
Also liegt der Fall a = xn und b < yn vor (siehe Aufgabe 6) mit d = 15 und x15 = 24 . Der Anziehende nimmt also von beiden Stapeln 1971 Münzen fort und hinterlässt seinem Gegner die Verlustposition (24,39) = (x15, y15) .
Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge
Publiziert 2011-12-30 Stand 2010-08-17
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite
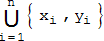

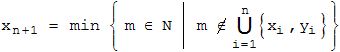
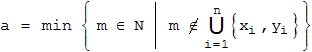
 1,62 rückt. So stellt sich die Vermutung ein, dass r = Φ ist. Φ steht für die Goldene Zahl:
1,62 rückt. So stellt sich die Vermutung ein, dass r = Φ ist. Φ steht für die Goldene Zahl:
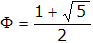
 Φ·n mit xn < Φ·n , und es liegt nahe, dass xn =
Φ·n mit xn < Φ·n , und es liegt nahe, dass xn =  Φ·n
Φ·n  . Dabei steht
. Dabei steht  .
.  für die ganzzahlige Abrundung.
für die ganzzahlige Abrundung.
 Φ·n
Φ·n  + n =
+ n =  Φ·n + n
Φ·n + n  =
=  ( Φ + 1 )·n
( Φ + 1 )·n  =
=  Φ2·n
Φ2·n  .
.
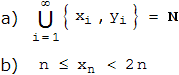
 a/Φ
a/Φ  · Φ
· Φ