Manfred Börgens - Problem 77 - Hinweis zu Aufgabe 5

x_n =  Φ·n 

Φ  ist die Goldene Zahl.

Wer den Beweis selbst führen möchte, kann sich an folgenden Schritten orientieren :

• Für die positiven irrationalen Zahlen  p, q  gelte  1/p + 1/q = 1 . (Das ist äquivalent zu  p + q = pq ; es folgt, dass eine der Zahlen im Intervall  (1, 2)  liegt und die andere in  (2, ∞). )
  Dann gilt für jede natürliche Zahl  a  entweder  a =  p·n   oder  a =  q·m   mit  n, m ∈ N .
  
  Dazu zeigt man zunächst, dass das „entweder“ gerechtfertigt ist.
  
  Aus  p > 1, q > 1  leitet man ab, dass in jedem Intervall  (a, a+1)  mit  a ∈ N  maximal ein  p·n  bzw.  q·m  liegt.
  
  Schließlich zeigt man, dass im Intervall  (1, a)  genau  a-1  Zahlen der Form  p·n  oder  q·m  liegen, was diesen Beweisschritt vervollständigt.
  
  
• p = Φ  und  q = Φ²  erfüllen die Bedingung  1/p + 1/q = 1 .
  
  
• Nun kann man zeigen, dass  x_n =  Φ·n   und  y_n =  Φ²·n   die Bedingungen
  
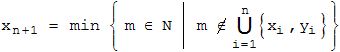
  und  y_n = x_n + n  erfüllen.
  
  Die zweite Bedingung wurde schon bei den Aufgaben 2 und 5 abgehandelt.

Manfred Börgens - Problem 77 - Hinweis zu Aufgabe 5


Publiziert 2011-11-30          Stand 2010-08-17

zurück zu Problem 77                   zur Leitseite