Manfred Börgens
Mathematische Probleme  # 77		 Liste aller Probleme mit Lösungen
voriges Problem      nächstes Problem		 zur Leitseite


Chinesisches Nim  -  Wijthoffs Spiel


Dies ist bereits das dritte Nim-Problem auf dieser Website (siehe # 46 und # 58). Es ist benannt nach Willem Abraham Wijthoff (1865 - 1939), einem niederländischen Mathematiker, der es 1907 beschrieben hat. Sehr häufig findet man es unter dem Namen Chinesisches Nim.

Robert Heidenreich hat dieses Spiel in seiner Bachelor-Thesis (2011) an der Technischen Hochschule Mittelhessen analysiert.

Hier ist die Spielregel: Zwei Spieler nehmen abwechselnd Münzen von zwei Stapeln weg. Die beiden Münzstapel enthalten bei Spielbeginn verschiedene Anzahlen  a  und  b  von Münzen. Der Spieler, der am Zuge ist, sucht sich entweder einen Stapel aus und entnimmt ihm beliebig viele Münzen, oder er nimmt von beiden Stapeln dieselbe Anzahl Münzen weg. Sieger des Spiels ist, wer die letzte Münze nimmt.

Wie auch andere Nim-Spiele ist Chinesisches Nim im Sinne der Spieltheorie ein neutrales oder objektives Spiel. Für jede Spielposition (a,b) gewinnt bei fehlerlosem Spiel entweder immer der Anziehende oder der Nachziehende.

Als Gewinnposition soll (a,b) gelten, wenn der Anziehende gewinnt; (a,b) heißt Verlustposition, wenn der Nachziehende gewinnt. Offenbar liegt bei  a = 0 , bei  b = 0  und bei  a = b  eine Gewinnposition vor. Eine Spielanalyse für kleine Werte von  a  und  b  zeigt schnell, dass es viel mehr Gewinn- als Verlustpositionen gibt. Es liegt also nahe, nur die Verlustpositionen zu bestimmen. Da es sich um abzählbar viele Positionen handelt, sollen sie übersichtlich angeordnet werden. Zunächst kann man immer  a < b  wählen. Die Werte von  a  für die Verlustpositionen sollen aufsteigend geordnet werden, wir wollen sie mit  xn  bezeichnen. Die zugehörigen Werte von  b  nennen wir dann  yn .


Aufgabe 1

Zeigen Sie: Alle Zahlen in den Paaren (xn , yn) kommen nur einmal vor, d.h.  xi ≠ xk , yi ≠ yk , xi ≠ yk   für  i ≠ k .

Von Hand oder mit einem kleinen Programm können Sie die ersten Folgenglieder (xn , yn) berechnen:


Erkennen Sie das Bildungsgesetz für diese Folge? Bei den  xn  muss man vielleicht etwas länger hinschauen, aber lesen Sie erst mal nicht weiter und versuchen Sie es selbst. Die Regel für  yn  erkennt man dann viel leichter.

Hier ist ein Tipp für die  xn : xn+1  ergibt sich aus dieser Vereinigungsmenge :

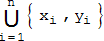
Formel 01


Aufgabe 2

Geben Sie eine rekursive Definition für die (xn , yn) an. Der Beweis kann mit vollständiger Induktion erfolgen.


Aufgabe 3

Folgerungen:

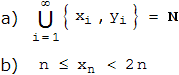
Formel 02



Mit einer Liste der (xn , yn) haben wir aber noch keine wirklich gute Strategie, um dieses Spiel zu gewinnen. Deshalb wollen wir der Frage nachgehen, ob es eine geschlossene Formel für (xn , yn) gibt. Es gibt sie tatsächlich, und sie ist recht einfach, aber nicht ganz leicht zu erkennen. Ausgangspunkt ist die Aufgabe 3 b). Offenbar ist  xn = q·n  mit  q ∈ [1, 2) . Aber  q  wird natürlich von  n  abhängen. Also bildet man  q = xn/n , um Genaueres über  q  herauszufinden (dafür braucht man natürlich eine längere Liste der  xn ; das geht zur Not noch von Hand, aber ein kleines Programm für die Rekursion aus Aufgabe 2 erspart Arbeit).


Aufgabe 4

Es gilt  xn/n ungefaehr gleich r , und  r  ist eine gut bekannte irrationale Zahl. Genauer:  lim xn/n = r  und  xn/n < r . Geben Sie eine Vermutung ab, welche Zahl  r  ist.

Setzt man also näherungsweise  xn ungefaehr gleich r·n , so ist immer  xn < r·n , aber nur mit einer geringen Differenz. Da  xn  ganzzahlig ist,  r·n  aber nicht, stellt sich nun die Vermutung über die geschlossene Formel ein:


Aufgabe 5

Stellen Sie (xn , yn) in geschlossener Form dar (erst mal ohne Beweis).

Natürlich lässt sich diese geschlossene Formel für die Verlustpositionen auch beweisen, aber es ist nicht ganz einfach, auf die richtige Beweisidee zu kommen. Deshalb gehört der Beweis nicht zur Aufgabenstellung. Wer ihn führen möchte und ein wenig Hilfe braucht, kann den Hinweis lesen.


Nun kommen wir zur Strategie für dieses Spiel. Was sollte der anziehende Spieler tun, wenn er die Spielposition (a,b) vorfindet? Zunächst wird er überprüfen, ob  (a,b) = (xn , yn)  ist. In diesem Falle ist er auf der Verliererstraße (wenn sein Gegner keinen Fehler macht). Ansonsten muss er Münzen von einem Stapel oder von beiden Stapeln so wegnehmen, dass er eine Verlustposition für seinen Gegner hinterlässt.


Aufgabe 6

Was ist die richtige Strategie für

Aufgabe 7

Für die Strategie in Aufgabe 6 ist es nützlich,  a = xn  bzw.  a = yn  möglichst leicht überprüfen zu können. Wie kann man das machen?


Aufgabe 8

Ein Beispiel: Wie verhalten Sie sich, wenn Sie bei (1995, 2010) am Zuge sind?



Lösung


Publiziert 2011-11-30          Stand 2010-08-05

voriges Problem   |   Liste aller Probleme mit Lösungen   |    nächstes Problem

Manfred Börgens   |    zur Leitseite                                     Datenschutz





ab 2020-06-25
www.boergens.de/manfred/problem/problem077.htm