Manfred Börgens - Problem 77 - Beweis Aufgabe 5
Zu zeigen ist: xn =  Φ·n
Φ·n 
Wir wiederholen zunächst den Text aus dem Hinweis, der die Einzelschritte des Beweises (s.u.) vorgeben soll:
- Für die positiven irrationalen Zahlen p, q gelte 1/p + 1/q = 1 . (Das ist äquivalent zu p + q = pq ; es folgt, dass eine der Zahlen im Intervall (1, 2) liegt und die andere in (2, ∞). )
Dann gilt für jede natürliche Zahl a entweder a =  p·n
p·n  oder a =
oder a =  q·m
q·m  mit n, m ∈ N .
mit n, m ∈ N .
Dazu zeigt man zunächst, dass das „entweder“ gerechtfertigt ist.
Aus p > 1, q > 1 leitet man ab, dass in jedem Intervall (a, a+1) mit a ∈ N maximal ein p·n bzw. q·m liegt.
Schließlich zeigt man, dass im Intervall (1, a) genau a-1 Zahlen der Form p·n oder q·m liegen, was diesen Beweisschritt vervollständigt.
- p = Φ und q = Φ2 erfüllen die Bedingung 1/p + 1/q = 1 .
- Nun kann man zeigen, dass xn =
 Φ·n
Φ·n  und yn =
und yn =  Φ2·n
Φ2·n  die Bedingungen
die Bedingungen
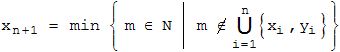
und yn = xn + n erfüllen.
Nun zum Beweis:
1.
 p·n
p·n  ≠
≠  q·m
q·m 
Annahme:  p·n
p·n  =
=  q·m
q·m  = a ∈ N ⇒ p·n = a + δ und q·m = a + ε mit δ, ε ∈ (0,1) ⇒ n = a/p + δ/p und m = a/q + ε/q ⇒ n + m = a + r mit r ∈ (0,1) (denn r ist ein gewichtetes Mittel von δ und ε ) ⇒ Wid. (denn n + m ∈ N, a + r ∉ N )
= a ∈ N ⇒ p·n = a + δ und q·m = a + ε mit δ, ε ∈ (0,1) ⇒ n = a/p + δ/p und m = a/q + ε/q ⇒ n + m = a + r mit r ∈ (0,1) (denn r ist ein gewichtetes Mittel von δ und ε ) ⇒ Wid. (denn n + m ∈ N, a + r ∉ N )
2.
In jedem Intervall (a,a+1) mit a ∈ N liegt maximal ein p·n bzw. q·m .
Wenn in (a,a+1) ein p·n liegt, dann liegt wegen 1. dort kein q·m , und umgekehrt. Es können aber auch nicht p·n1 und p·n2 in (a,a+1) liegen, da p > 1 ; das Analoge gilt für q·m .
3.
Im Intervall (1, a) liegen genau a - 1 Zahlen der Form p·n oder q·m .
Von den Zahlen p·n liegen nur endlich viele unterhalb von a ∈ N . Das maximale n mit dieser Eigenschaft nennen wir nmax .
p·nmax < a ⇒ nmax < a/p ⇒ nmax =  a/p
a/p  .
Analog folgt: mmax =
.
Analog folgt: mmax =  a/q
a/q  .
.
Also liegen in (1, a) insgesamt  a/p
a/p  +
+  a/q
a/q  Exemplare der p·n bzw. q·m .
Exemplare der p·n bzw. q·m .
Mit geeigneten δ, ε ∈ (0,1) gilt dann:
 a/p
a/p  +
+  a/q
a/q  = a/p - δ + a/q - ε = a - δ - ε = a - 1 , da in der Gleichung nur natürliche Zahlen auftreten und δ + ε ∈ (0,2) .
= a/p - δ + a/q - ε = a - δ - ε = a - 1 , da in der Gleichung nur natürliche Zahlen auftreten und δ + ε ∈ (0,2) .
4.
Wegen Φ + 1 = Φ2 gilt 1/Φ + 1/Φ2 = 1 .
5.
Zur Minimum-Bedingung für xn+1 :
Die Zahlenfolgen xn =  Φ·n
Φ·n  und yn =
und yn =  Φ2·n
Φ2·n  sind disjunkt und streng monoton wachsend, deshalb gilt:
sind disjunkt und streng monoton wachsend, deshalb gilt:
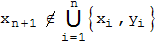
Die Zahlen, die kleiner als xn+1 sind, sind die kleineren xi mit i ≤ n , und einige der yi mit i ≤ n (da xi < yi ) und liegen somit in der Vereinigungsmenge. xn+1 ist deshalb das gesuchte Minimum. Das kann man auch grafisch veranschaulichen:

Anhand der Grafik kann man das folgende Beispiel nachvollziehen:
x12 liegt nicht in der Vereinigung der {xi, yi} für i ≤ 11 , da die xi streng monoton wachsen und xi ≠ yj gilt. x12 ist die kleinste Zahl mit dieser Eigenschaft, da alle kleineren entweder ein xi oder ein yi mit i ≤ 11 sein müssen, denn die beiden Zahlenfolgen decken ganz N ab.
Die Bedingung yn = xn + n wurde schon bei den Aufgaben 2 und 5 abgehandelt. Zurück zu Problem 77.
Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge
Manfred Börgens - Problem 77 - Beweis Aufgabe 5
Publiziert 2011-12-30 Stand 2010-08-17
zurück zu Problem 77 zur Leitseite
 Φ·n
Φ·n 
 Φ·n
Φ·n 
 p·n
p·n  oder a =
oder a =  q·m
q·m  mit n, m ∈ N .
mit n, m ∈ N .
 Φ·n
Φ·n  und yn =
und yn =  Φ2·n
Φ2·n  die Bedingungen
die Bedingungen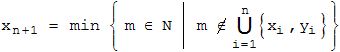
 p·n
p·n  ≠
≠  q·m
q·m 
 p·n
p·n  =
=  q·m
q·m  = a ∈ N ⇒ p·n = a + δ und q·m = a + ε mit δ, ε ∈ (0,1) ⇒ n = a/p + δ/p und m = a/q + ε/q ⇒ n + m = a + r mit r ∈ (0,1) (denn r ist ein gewichtetes Mittel von δ und ε ) ⇒ Wid. (denn n + m ∈ N, a + r ∉ N )
= a ∈ N ⇒ p·n = a + δ und q·m = a + ε mit δ, ε ∈ (0,1) ⇒ n = a/p + δ/p und m = a/q + ε/q ⇒ n + m = a + r mit r ∈ (0,1) (denn r ist ein gewichtetes Mittel von δ und ε ) ⇒ Wid. (denn n + m ∈ N, a + r ∉ N )
 a/p
a/p  .
Analog folgt: mmax =
.
Analog folgt: mmax =  a/q
a/q  .
.
 a/p
a/p  +
+  a/q
a/q  Exemplare der p·n bzw. q·m .
Exemplare der p·n bzw. q·m .
 a/p
a/p  +
+  a/q
a/q  = a/p - δ + a/q - ε = a - δ - ε = a - 1 , da in der Gleichung nur natürliche Zahlen auftreten und δ + ε ∈ (0,2) .
= a/p - δ + a/q - ε = a - δ - ε = a - 1 , da in der Gleichung nur natürliche Zahlen auftreten und δ + ε ∈ (0,2) .
 Φ·n
Φ·n  und yn =
und yn =  Φ2·n
Φ2·n  sind disjunkt und streng monoton wachsend, deshalb gilt:
sind disjunkt und streng monoton wachsend, deshalb gilt: