
Dominica 1999 Michel 2762
Fibonacci-Quadrate und Fibonacci-Rechtecke
Die Lösung steht im unteren Teil der Seite.
Fibonacci (Leonardo da Pisa, ca. 1170 - ca. 1250) gilt als einer der bedeutendsten europäischen Mathematiker des Mittelalters. Er lebte in einer Zeit, in der die arabische Mathematik erheblich fortgeschrittener als die europäische war. In der riesigen von Muslimen beherrschten Welt - von Portugal bis an die Grenzen Chinas - wurde die griechische Mathematik der Antike bewahrt und weiterentwickelt.
Fibonacci war Rechenmeister in Pisa. Besonders bekannt sind heute die nach ihm benannten Fibonacci-Zahlen. Aber seine Bedeutung lag vor allem in der Einführung des indisch-arabischen Zahlsystems in die europäische Kaufmannschaft. Fibonacci wurde als junger Mann mit der arabischen Mathematik vertraut, als er seinen Vater nach Algerien begleitete (ins heutige Bejaia); dieser vertrat dort die Pisaner Kaufmannschaft als Notar. Später bereiste Fibonacci große Teile der Mittelmeerraums - Ägypten, Syrien, Griechenland, Sizilien und Südfrankreich - und überall versuchte er, sich weitere mathematische Kenntnisse anzueignen.
Ein Hauptwerk Fibonaccis ist das Rechenbuch Liber abbaci. Es behandelt ausführlich die Arithmetik und Algebra mit den indisch-arabischen Zahlen: Bruchrechnung, Dreisatz, arithmetische und geometrische Reihen, Systeme von linearen Gleichungen, Zinsrechnung, Quadrat- und Kubikwurzeln, quadratische Gleichungen. Fibonacci gibt im Liber abbaci nicht nur Rechenanleitungen und viele Beispiele, sondern leistet auch eine theoretische Durchdringung der Materie und gibt Beweise seiner Lehrsätze an. Die langfristige Wirkung dieses Werks auf die europäische Mathematik ist nicht zu unterschätzen; allerdings wurde das neue Zahlsystem nur allmählich akzeptiert. Dies lag sicherlich auch daran, dass Fibonaccis Rechenbuch nur in handgeschriebenen Kopien kursierte - 300 Jahre später, nach der Erfindung des Buchdrucks, hatten es die Rechenmeister Luca Pacioli, Adam Riese und Simon Stevin wesentlich einfacher, ihre Rechenbücher schnell zu verbreiten.
Das aus heutiger Sicht beeindruckendste Werk Fibonaccis ist Liber quadratorum, ein Buch über Zahlentheorie. Wahrscheinlich ist Fibonacci der Erste gewesen, der die Quadratzahlen als Summe konsekutiver ungerader Zahlen erkannte. Diese und andere (damals neue) zahlentheoretische Erkenntnisse finden sich im Liber quadratorum, das jedoch lange Zeit völlig unbekannt blieb.
Weitere Bücher von Fibonacci sind der Arithmetik und der Geometrie gewidmet: Practica geometriae, Flos super solutionibus quarumdam questionum ad numerum et ad geometriam vel ad utrumque pertinentium, Di minor guisa und ein verschollener Kommentar zu Band 10 von Euklids Elementen.
Der kleine karibische Inselstaat Dominica hat für die Fibonacci-Briefmarke ein Phantasie-Porträt gewählt, da niemand genau weiß, wie Leonardo da Pisa ausgesehen hat.
Die Fibonacci-Zahlen
Nach Fibonacci ist eine der bekanntesten Zahlenfolgen benannt. Er behandelte sie nur beiläufig in Liber abbaci, im Zusammenhang mit der Vermehrung von Kaninchen. Die Fibonacci-Zahlen lauten:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Formal schreibt man für die Folge (Fn)nεN , d.h. F1 = 1 , F2 = 1 , ... F9 = 34 usw.
Die Fibonacci-Zahlen folgen einer einfachen Gesetzmäßigkeit: Jede von ihnen (ab der dritten) ist die Summe der beiden Vorgänger:
F1 = F2 = 1 , Fn+2 = Fn+1 + Fn
Die Fibonacci-Folge hat eine Vielzahl interessanter und verblüffender Eigenschaften und spielt eine wichtige Rolle in der Zahlentheorie. Zahlreiche Internet-Seiten sind ihr gewidmet, z.B. die sehr informative Website von Ron Knott. Mein "Problem-Kollege" Olivier Rochoir aus Frankreich hat eine schöne Aufgabe gestellt, die mit Hilfe der Fibonacci-Zahlen gelöst werden kann; die deutsche Übersetzung lautet:
Um zu meiner Wohnung zu gelangen, muss ich eine Treppe mit 40 Stufen hinaufgehen.
Manchmal überspringe ich eine Stufe. Um genau zu sein: Bei jedem Schritt habe ich
die Wahl, meinen Fuß entweder auf die nächste oder die übernächste Stufe zu setzen.
Wieviele verschiedene Möglichkeiten gibt es für mich, meine Treppe hinaufzugehen?
Die Fibonacci-Zahlen und der Goldene Schnitt
Auf der Briefmarke sieht man Φ , den griechischen Großbuchstaben Phi. Er steht für die Zahl des Goldenen Schnitts, Φ = ( 51/2 + 1 )/ 2 = 1,618... . Φ steht in einem engen Zusammenhang mit den Fibonacci-Zahlen. Um diesen aufzudecken, soll zunächst eine geschlossene Formel für Fn angegeben werden. Die oben angegebene rekursive Formel für die Fibonacci-Folge ist eine lineare, homogene Differenzengleichung 2. Ordnung mit konstanten Koeffizienten: Fn+2 - Fn+1 - Fn = 0 . Das zugehörige charakteristische Polynom λ2 - λ - 1 hat die Nullstellen Φ und - φ mit φ = 1/Φ = Φ - 1 = 0,618... (φ ist der griechische Kleinbuchstabe phi). Also ist die Lösung der Differenzengleichung Fn = C1·Φn + C2·(-φ)n . C1 und C2 berechnet man mit den Anfangswerten F1 = F2 = 1 zu C1,2 = +- 5-1/2 und erhält so eine geschlossene Formel für die Fibonacci-Zahlen:
Fn = ( Φn - (-φ)n ) / 51/2
Aus dieser Formel ergibt sich die noch einfachere Definition (rd(.) steht für die Rundung auf die nächstgelegene ganze Zahl):
Fn = rd( Φn/51/2 )
Ferner ergibt sich Φ als Grenzwert von Fn+1 / Fn .
Aufgabe 1
Sowohl mit der aus der Differenzengleichung hergeleiteten Formel für Fn als auch rekursiv mit Fn+2 - Fn+1 - Fn = 0 lässt sich die Fibonacci-Folge in die andere Richtung fortsetzen; man erhält F0 = 0 , F-1 = 1 usw. Wie lässt sich F-n mit Hilfe von Fn ausdrücken?
|
Die "Fibonacci-Rechtecke" und die "Fibonacci-Spirale"
Für die Produkte zweier aufeinanderfolgender Fibonacci-Zahlen gibt es eine Formel, die sich sehr schön geometrisch veranschaulichen lässt. Man nimmt eine Folge von Quadraten, deren Seitenlängen die Fibonacci-Zahlen sind. Diese Quadrate setzt man sukzessive zu Rechtecken zusammen; hat man n Quadrate zu einem Rechteck zusammengefügt, legt man das (n+1)-te Quadrat an der längeren Rechteckseite an. Das geht, weil das n-te Rechteck die Seitenlängen Fn und Fn + Fn-1 = Fn+1 hat (einfache Induktion). In Bild 1 liegt das erste Quadrat oben links; danach wurde immer abwechselnd unten und rechts angelegt. Das n-te Rechteck hat dann den Flächeninhalt Fn·Fn+1 , dieser ist also gleich der Summe der ersten n Fibonacci-Quadrate.
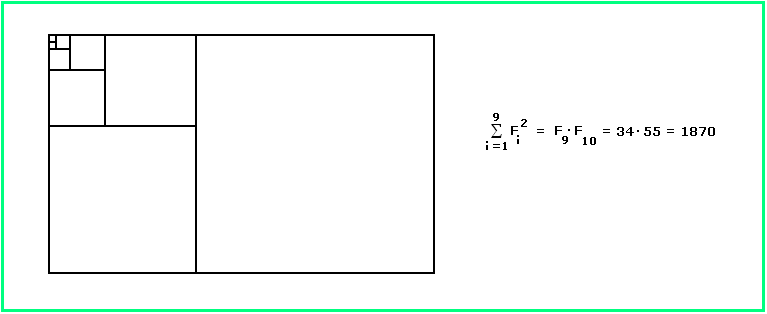
Bild 1
Aufgabe 2
Beweisen Sie Σi = 1..n Fi2 = Fn · Fn+1 (nicht geometrisch, sondern durch Rechnung).
|
Diese Formel mit der einprägsamen geometrischen Interpretation ist aber nicht lediglich eine Folgerung aus der Definition der Fibonacci-Zahlen, sondern kann umgekehrt auch selbst als Definition der Fibonacci-Zahlen dienen. Was die Anfangswerte angeht, ist sie sogar einfacher:
Aufgabe 3
Zeigen Sie die Äquivalenz von Fn+2 = Fn+1 + Fn und Σi = 1..n Fi2 = Fn · Fn+1 zur Definition der Fibonacci-Zahlen.
Formulieren Sie dabei die Anfangswerte möglichst sparsam.
|
Wir wollen die Rechtecke wie in Bild 1 "Fibonacci-Rechtecke" nennen. Mit wachsender Größe nähert sich ihr Format wegen lim Fn+1 / Fn = Φ dem Goldenen Schnitt. Wählt man eine andere, nämlich spiralige Anordnung der Quadrate, gelangt man zu einem Bild, das in ganz ähnlicher Form für die Veranschaulichung der Logarithmischen Spirale auf der Briefmarke #5 zu sehen ist (dort haben die Rechtecke nicht nur näherungsweise, sondern exakt das Format des Goldenen Schnitts, sie sind also "Goldene Rechtecke"). Was heißt "spiralige Anordnung"? In Bild 1 hatten wir die Quadrate immer abwechselnd unten und rechts angelegt; wenn man sie unten-rechts-oben-links-unten ... anlegt, liegen sie spiralig wie in Bild 2 (die Größe der Fibonacci-Rechtecke ändert sich dadurch nicht). Die grüne Spirale in Bild 2 entsteht durch eine Folge von Viertelkreisen, wir wollen sie "Fibonacci-Spirale" nennen. Sie sieht der Logarithmischen Spirale auf den ersten Blick recht ähnlich. Auch dort verbindet die Spirale eine Folge von Punkten, die auf den Ecken von spiralig angeordneten Quadraten liegen - nach der gleichen Konstruktion wie bei der Fibonacci-Spirale. Es gibt aber zwei Unterschiede: Beim Start der Konstruktion beginnt man bei der Fibonacci-Spirale mit einem Quadrat, bei der Logarithmischen Spirale mit einem Goldenen Rechteck; ferner besteht die Logarithmische Spirale nicht aus Viertelkreisen, auch wenn das in den kleineren Quadraten kaum unterscheidbar ist (siehe die Diskussion zu Briefmarke #5). Da aber die Fibonacci-Rechtecke mit wachsender Anzahl der Quadrate im Format den Goldenen Rechtecken immer ähnlicher werden, ist zumindest die Folge der Spiralpunkte auf den Quadratecken für die beiden Spiraltypen mit wachsender Windungszahl immer weniger unterscheidbar.
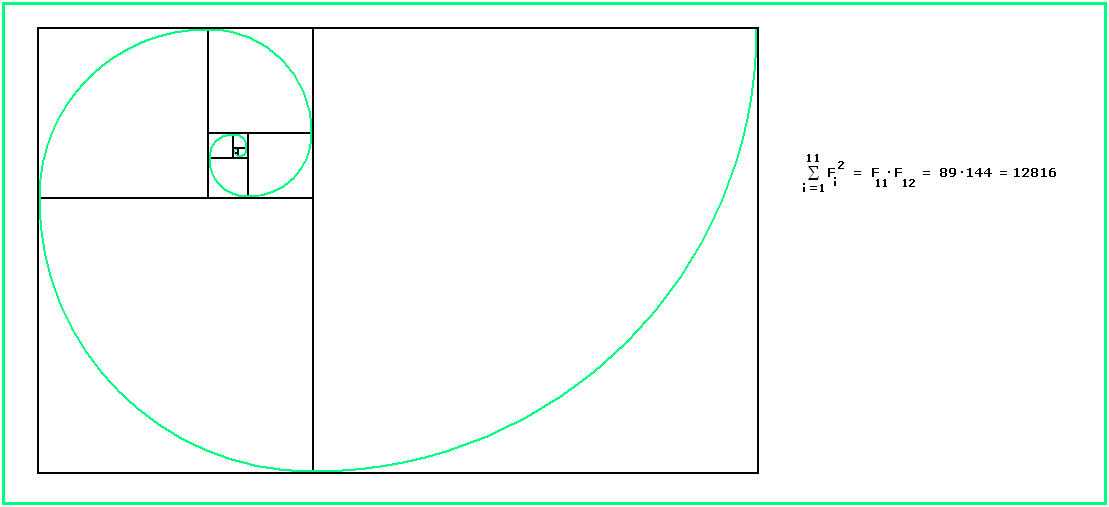
Bild 2
Hier ist eine Privatmarke, die die Fibonacci-Zahlen, die Fibonacci-Rechtecke und die Fibonacci-Spirale zeigt:

Lösung
Aufgabe 1
Wir rechnen die ersten Fibonacci-Zahlen mit negativen Indizes aus:
..., -21, 13, -8, 5, -3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, ...
Sofort stellt sich die Vermutung ein: F-n = (-1)n+1 · Fn
Erster Beweis: Vollständige Induktion
Den richtigen Induktionsanfang haben wir eben schon gesehen. Ist nun die Vermutung für alle Indizes von 0 bis n richtig, so gilt:
F-(n+1) = F-(n-1) - F-n = (-1)n · Fn-1 - (-1)n+1 · Fn = (-1)n+2 ·( Fn-1 + Fn ) = (-1)n+2 · Fn+1
Zweiter Beweis: Mit Lösung der Differenzengleichung
F-n = ( Φ-n - (-φ)-n ) / 51/2 = ( φn - (-Φ)n ) / 51/2 = (-1)n+1 ·( Φn - (-φ)n ) / 51/2 = (-1)n+1 · Fn
Aufgabe 2
Beweis durch vollständige Induktion über n :
Der Induktionsanfang ( n = 1 ) ist klar, denn F12 = F1 · F2 .
Induktionsschritt n --> n + 1 : Σi = 1..n+1 Fi2 = Fn · Fn+1 + Fn+12 = Fn+1·( Fn + Fn+1 ) = Fn+1 · Fn+2
Aufgabe 3
Wir haben in Aufgabe 2 gezeigt, dass aus F1 = F2 = 1 , Fn+2 = Fn+1 + Fn folgt: Σi = 1..n Fi2 = Fn · Fn+1 .
Beginnt man umgekehrt mit Σi = 1..n Fi2 = Fn · Fn+1 , so erkennt man, dass schon die Anfangsbedingung F1 = 1 ausreicht, um sukzessive alle weiteren Folgenglieder zu berechnen, denn offenbar ergibt sich das (n+1)-te Folgenglied aus den ersten n . Dass dann auch wirklich die Fibonacci-Folge entsteht, müssen wir noch zeigen:
Fn + Fn+1 = ( Fn · Fn+1 + Fn+12 ) / Fn+1 = Σi = 1..n+1 Fi2 / Fn+1 = ( Fn+1 · Fn+2 ) / Fn+1 = Fn+2
Wir haben also bewiesen, dass die beiden folgenden Definitionen der Fibonacci-Zahlen äquivalent sind:
F1 = F2 = 1 , Fn+2 = Fn+1 + Fn
F1 = 1 , Σi = 1..n Fi2 = Fn · Fn+1
weitere Biografie: Fibonacci
Kategorie: Zahlen und Zahlsysteme, Berechnung von π
Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge
Kategorie: Arabische Mathematik
Publiziert 2008-06-15 Stand 2023-01-11
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite



