Italien 2000   Michel 2726   Scott 2373

Bisher vorgestellte Briefmarken zum Weltjahr der Mathematik 2000:         →   Tschechien               Marke # 1         →   Kroatien                 Marke # 97         →   Belgien und Argentinien  Marke # 121  mit allgemeiner Einführung zum WMY 2000         →   Luxemburg                Marke # 122  mit Erläuterung des Logos         →   Spanien und Slowakei     Marke # 123         →   Monaco und Südkorea      Marke # 124

Italien


Dies ist der letzte Beitrag auf dieser Website zum WMY 2000. Die dargestellte Marke zeigt das WMY-2000-Logo, das bei der Marke aus Luxemburg erläutert wurde, im Hintergrund offenbar eine fraktale Menge und rechts unten ein geometrisches Objekt, das den Bezug zu Italien, dem Herausgeberland, herstellt. Die geometrische Darstellung zeigt eine Kugel mit umbeschriebenem Zylinder und führt in der Mathematikgeschichte weit zurück zu Archimedes von Syrakus (287 - 212 v. Chr.), der auf dieser Website bereits mit der Briefmarke # 33 vorgestellt wurde. Die Briefmarke # 103 wurde zum Archimedischen Jahr herausgegeben.

Archimedes fand mehrere Lehrsätze zur ebenen und räumlichen Geometrie und führte die Beweise oft mit infinitesimalen Methoden, lange bevor diese in der heute üblichen Strenge formuliert wurden. Für Kugel und Zylinder fand er zwei Zusammenhänge, auf die er so stolz war, dass die "Kugel im Zylinder" seinen Grabstein schmücken sollte:

Das Volumen einer Kugel beträgt  2/3  des Volumens des umbeschriebenen Zylinders.

Die Oberfläche einer Kugel hat den gleichen Flächeninhalt wie die Mantelfläche des umbeschriebenen Zylinders.

Für das Volumen gibt es in den Schriften des Archimedes zwei Beweise. Der erste folgt der "mechanischen Methode" (von ihm so benannt). Das zugehörige Buch wurde erst 1906 von Johan Heiberg in Konstantinopel gefunden. Archimedes verwendete in diesem Beweis die von ihm formulierten Hebelgesetze und einen Lehrsatz des Eudoxos von Knidos (408 - 355 v. Chr.):

Das Volumen eines Kegels beträgt  1/3  des Volumens des umbeschriebenen Zylinders.

Diesen Satz und seinen Beweis hat Euklid in seine Elemente aufgenommen, siehe [1, 12. Buch, 10. Satz]  (Quellen am Ende dieser Seite).

Archimedes hängte eine Kugel und einen Kegel an eine Seite einer Balkenwaage und einen Zylinder an die andere Seite; alle drei Körper mit der gleichen Höhe. Für einen bestimmten (sehr kleinen) Bruchteil dieser Höhe zerlegte er die Körper in entsprechend dünne Scheiben, deren Volumen er näherungsweise als proportional zum Flächeninhalt von Kreisen annahm, und bewies ein Gleichgewicht der Waage für diese Scheiben. Ausführlich und in den Worten von Archimedes (in deutscher Übersetzung) wird dieses Verfahren in [7, ab S. 46] gezeigt. Kompaktere Fassungen in moderner Sprache findet man in [3] und [6]. Damit gelangte Archimedes zu den Aussagen:

Die Volumina von Halbkugel und Kegel (mit gleicher Grundfläche und gleicher Höhe) ergeben in der Summe das Volumen des umbeschriebenen Zylinders.

Anders formuliert:

Die Volumina von Kugel und einbeschriebenem Doppelkegel ergeben in der Summe das Volumen des umbeschriebenen Zylinders.

Mit dem Lehrsatz des Eudoxos folgt daraus:

Die Volumina von Doppelkegel mit quadratischem Querschnitt, umbeschriebener Kugel und umbeschriebenem Zylinder verhalten sich wie  1:2:3 .

Durch die Verwendung "dünner" Scheiben, die auf jeweils gleicher Höhe aus verschiedenen Körpern ausgeschnitten wurden und deren Volumina als Flächeninhalte aufgefasst werden konnten, nahm Archimedes das Prinzip von Cavalieri vorweg, das in moderner Zeit zu einem Bestandteil der Integralrechnung wurde.  —  Archimedes hätte es sich aber etwas einfacher machen können, denn seine Beweisidee enthielt im Prinzip die "moderne" Variante des "1:2:3-Satzes", wie das folgende Bild mit den Querschnitten von Kegel, Zylinder und Halbkugel (alle mit gleichem Basisradius r und gleicher Höhe r) zeigt:



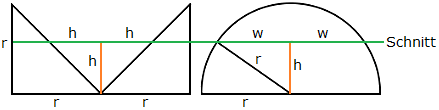
Hier ist der Kegel aus dem Zylinder ausgeschnitten, so dass nur gezeigt werden muss, dass mit Cavalieri für jeden horizontalen Schnitt die linke und die rechte Schnittfläche den gleichen Flächeninhalt haben.

Matroids Matheplanet gibt Archimedes in [4] als direkten Urheber dieser Idee an, allerdings ohne Quellenangabe.

Die linke Schnittfläche ist ein Kreisring mit Außenradius  r  und Innenradius  h ,  sie hat also den Flächeninhalt  π·(r²-h²). Die rechte Schnittfläche ist ein Kreis mit Radius  w  und Flächeninhalt  π·w² = π·(r²-h²).

Archimedes war mit seinem Beweis nicht recht zufrieden, weil ihm seine Verwendung des Cavalieri-Prinzips und der Wägung von Schichten unzureichend begründet erschien. Aber er kannte die Exhaustionsmethode des Eudoxos (der uns schon weiter oben begegnet ist), mit der er seinen "1:2:3-Volumen-Satz" bestätigen und außerdem die Gleichheit der Flächeninhalte der Kugeloberfläche und der Mantelfläche des Zylinders beweisen konnte.

Bei der Exhaustionsmethode legt Archimedes regelmäßige  4n-Ecke in den und um den Kugelquerschnitt; deren Drehkörper bestehen dann aus  2n  Kegelstümpfen, deren Volumina und Mantelflächen er berechnet. Mit wachsendem  n  approximieren diese das Kugelvolumen und die Kugeloberfläche. Ausführlich und in den Worten von Archimedes (in deutscher Übersetzung) wird dieses Verfahren in [2, S. 10 - 14] beschrieben. Kompaktere Fassungen in moderner Sprache findet man in [5] und [6].


Quellen

[1]  Euklid:  Elemente, übersetzt von Lorenz, J.F.  Buchhandlung des Waysenhauses, Halle 1781.   →   Sächsische Landesbibliothek - Staats- und Universitätsbibliothek Dresden

[2]  Gutenäcker, J.:  Das Grabmal des Archimedes. Festschrift 1833.   →   bavarikon

[3]  Herder-Oberschule:  Das Kugelvolumen oder, ... was ist das Geheimnis des Grabsteins des Archimedes

[4]  Matroids Matheplanet:  Über Kegel, Pyramiden und Kugeln

[5]  Petritsch,T.:  Flächen und Volumina in Frühzeit und Antike. Diplomarbeit 2020.   →   Universität Graz

[6]  Ruppert, M.:  Archimedes, der Kreis und die Kugel. mathematik lehren 165 (2011), S. 48 - 53.   →   Universität Würzburg

[7]  Wieleitner, H.:  Infinitesimalrechnung. G. Braun, Karlsruhe, 2. Aufl. 1924.   →   RCIN

Publiziert 2023-10-23          Stand 2021-05-01