Spanien 2000   Michel 3542                                                Slowakei 2000   Michel 365   Scott 352

Bisher vorgestellte Briefmarken zum Weltjahr der Mathematik 2000:         →   Tschechien               Marke # 1         →   Kroatien                 Marke # 97         →   Belgien und Argentinien  Marke # 121                    mit allgemeiner Einführung zum WMY 2000         →   Luxemburg                Marke # 122                    mit Erläuterung des Logos

In diesem Beitrag werden die beiden WMY-2000-Briefmarken gezeigt, mit denen Mathematiker von ihren Herkunftsländern geehrt wurden. Die drei abgebildeten Mathematiker haben eine gemeinsame Eigenschaft: Sie waren in ihren Ländern Pioniere beim Aufbau von Hochschulen, Akademien und mathematischen Fakultäten.


Spanien

Julio Rey Pastor (1888 - 1962)

Neben dem Logo des WMY 2000 ist der spanische Mathematiker Julio Rey Pastor porträtiert. Nach der Promotion in algebraischer Geometrie 1910 in Madrid wurde Rey Pastor Professor in Oviedo. In den nächsten Jahren reiste er wiederholt zu Forschungsaufenthalten nach Berlin und Göttingen. Er erkannte die Rückständigkeit der spanischen Mathematikausbildung und erreichte 1915, dass Spanien ein eigenes mathematisches Forschungsinstitut gründete, um das Land an den europäischen Standard heranzuführen. Zu dieser Zeit verließ er Oviedo und lehrte bis 1917 an den Universitäten Madrid und Barcelona. Er folgte dann einem Ruf nach Buenos Aires, erst zu Gastaufenthalten, später auf einer permanenten Position, und pendelte für den Rest seines Lebens (45 Jahre lang) zwischen Argentinien und Spanien. In Argentinien leistete er die gleiche Aufbauarbeit wie vorher in Spanien durch den Aufbau eines Forschungsseminars für Mathematik und die Gründung der Argentinischen Mathematischen Vereinigung. In beiden Ländern sah sich Rey Pastor erheblichen Widerständen aus der etablierten Mathematikerschaft gegenüber, war aber bei seinen Studierenden beliebt. Sein Forschungsinteresse richtete sich u.a. auf Konvergenzprobleme bei unendlichen Summen und Integralen.


Slowakei

Juraj Hronec (1881 - 1959) und  Štefan Schwarz (1914 - 1996)

Juraj Hronec (meist wird nur Jur als Vorname genannt) war ein slowakischer Mathematiker, der zeitweise in Deutschland studierte und 1912 an der Universität Gießen promovierte. Seine Dissertation und seine spätere Forschung behandelte die Theorie der Differentialgleichungen. Nach seiner Habilitation in Prag 1923 arbeitete Hronec bis 1939 als Professor in Brünn.  —  Hronec wirkte als Initiator für den Aufbau mehrerer slowakischer Hochschulen, an denen er auch selbst als Professor und Rektor oder Dekan wirkte, und erwarb sich Verdienste um die Stärkung der akademischen Mathematik in der Slowakei. Als Hochschullehrer galt sein Hauptinteresse der Didaktik der Mathematik und den Anwendungen in den technisch orientierten Studiengängen.

Štefan Schwarz war ein slowakischer Mathematiker, der in Prag studierte und dort 1937 seine Promotion über endliche Körper abschloss. Noch im gleichen Jahr sah er sich als Jude gezwungen, Prag zu verlassen und in die Slowakei zurückzukehren. Bis 1944 arbeitete Schwarz als Professor an der TU Pressburg. Er überlebte die Internierung in den Konzentrationslagern Sachsenhausen und Buchenwald und kehrte wieder an die TU Pressburg zurück. Seine Forschungstätigkeit umfasste Algebra (u.a. endliche Körper und Halbgruppen) und Zahlentheorie.  —  Wie schon Juraj Hronec vor ihm, arbeitete Schwarz, der als exzellenter Lehrer anerkannt war, nach dem Weltkrieg am Aufbau des Hochschulwesens in der Slowakei und als Herausgeber und Autor mathematischer Zeitschriften.  —  Erfreulicherweise enthält die Briefmarke außer den Porträts noch eine mathematische Grafik. Sie zeigt den endlichen Körper \(~F_{2^{30}}~\) mit allen seinen Unterkörpern (und deren Unterkörpern).


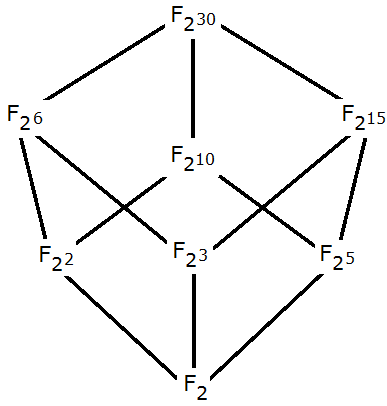
                           Endliche Körper \(~F_{2^{~m}}~\) mit \(~m|30~\)

Endliche Körper haben \(~p^n~\) Elemente, mit \(~p~\) prim und \(~n \in \textbf{N}~\); zu jedem \(~q=p^n~\) gibt es genau einen Körper mit \(~q~\) Elementen, der mit \(~F_{p^n}~\) bezeichnet wird. Die Unterkörper von \(~F_{p^n}~\) sind \(~F_{p^m}~\) mit \(~m|n~~\) (\(~m~\) ist Teiler von \(~n~\)).

Auf dem Ersttagsbrief erscheint im Bild links unten der Hinweis auf die Union slowakischer Mathematiker und Physiker (Jednota Slovenskych Matematikov a Fyzikov):

Publiziert 2023-04-24          Stand 2023-08-11