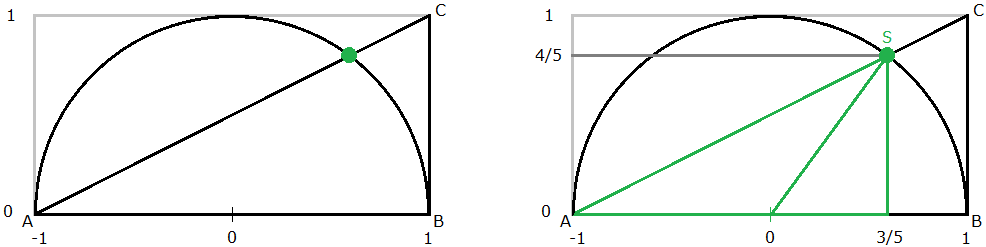Monaco 2000   Michel 2518   Scott 2175           Südkorea 2000   Michel 2104   Scott 2026

Bisher vorgestellte Briefmarken zum Weltjahr der Mathematik 2000:         →   Tschechien               Marke # 1         →   Kroatien                 Marke # 97         →   Belgien und Argentinien  Marke # 121                    mit allgemeiner Einführung zum WMY 2000         →   Luxemburg                Marke # 122                    mit Erläuterung des Logos         →   Spanien und Slowakei     Marke # 123

Monaco

Auf dieser Briefmarke spielt die Zahl \(~5~\) eine sehr dominante Rolle, auch in den "Einkleidungen" \(~\sqrt{5}~\) und \(~\Phi=(1+ \sqrt{5})/2~\) (Goldene Zahl). Dies wird weiter unten ausführlich behandelt.  —  Der Designer hat außerdem die ganzen Zahlen \(~0~...~9~\),  die Zahl \(~\pi~\) und einen Ausschnitt aus einem Schachbrett mit der Figur einer Dame dargestellt. Bis auf die Konstruktion oben rechts sind alle Motive der Marke von einem Quadrat umgeben. In diesem steht der Vitruvianische Mensch, hier in einer Zeichnung von Leonardo da Vinci. Seine Füße ruhen auf einem Kreisbogen. In dieser Darstellung eines menschlichen Körpers finden sich nach ihrem Urheber, dem römischen Architekten Vitruvius, einfache und regelmäßige mathematische Proportionen.

Nun zur Zahl \(~5~\).  Das auffälligste Motiv der Briefmarke ist sicherlich das Dodekaeder, ein Platonischer Körper, dessen Oberfläche aus zwölf kongruenten regelmäßigen Fünfecken besteht. Im Dodekaeder findet man die Goldene Zahl \(~\Phi=(1+ \sqrt{5})/2~\) in den Verhältnissen  Umkugelradius/Kantenlänge\(~=~\Phi \cdot \sqrt{3} /2~\) und  Volumen_Dodekaeder/Volumen_Umkugel\(~=~\Phi \cdot \sqrt{5/3}/ \pi~\).

Die Skizze rechts oberhalb des Quadrates und unterhalb der Portoangabe zeigt eine geometrische Konstruktion aus einem rechtwinkligen Dreieck, einem großen Halbkreis und einem kleinen Kreis. Wir können erschließen, dass die Höhe des Dreiecks und der Radius des Halbkreises \(~=1~\) und der Radius des kleinen Kreises \(~=1/2~\) sein müssen (siehe unten); in den Bildern 1 und 2 wurde die Skizze in ein Koordinatensystem gelegt, das diese Maße wiedergibt. Wir berechnen zuerst den Schnittpunkt \(~S~\) der Hypotenuse mit dem Halbkreis. In Bild 1 ist der kleine Kreis weggelassen worden; die Punkte \(~A,B,C~\) sind aus der Skizze auf der Marke übernommen worden. Es stellt sich heraus, dass \(~S~\) rationale Koordinaten \((3/5,~4/5)\) hat; das kleine grüne rechtwinklige Dreieck, dessen Hypotenuse vom Nullpunkt nach \(~S~\) läuft, ist also ein pythagoreisches Dreieck mit den Seitenverhältnissen \(~3:4:5~\).  Das große grüne rechtwinklige Dreieck mit der Hypotenuse \(~AS~\) hat die Hypotenusenlänge \(~\sqrt{5} \cdot 4/5~\).  Zum Beweis, dass \(~S=(s_1,s_2)=(3/5,~4/5)~\) ist (alle anderen Angaben folgen daraus), stellt man die Gleichungen \(~1+s_1=2\cdot s_2~\) (Strahlensatz mit \(~AB=2 \cdot BC~\)) und \(~s_1^2+s_2^2=1~\) auf.



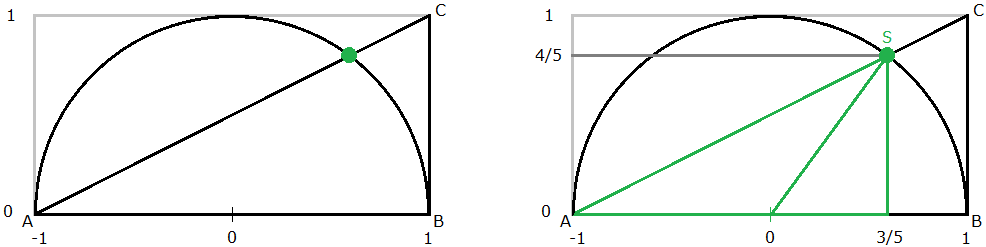
Bild 1

Zum kleinen Kreis in der oberen Skizze auf der Briefmarke gehören die Punkte \(~H~\) und \(~K~\) und die Formel \(~AK=1,618=\Phi~\) neben dem Kopf. (Der Graphiker verwendet den kleinen Buchstaben  φ  für die Goldene Zahl, aber wir bleiben bei der üblichen Konvention). Das bedeutet, dass hier eine geometrische Konstruktion für die Goldene Zahl angegeben wird (zum Vergleich mit anderen Konstruktionen siehe Briefmarke # 72). Zu dieser Konstruktion gehört Bild 2, wo der Halbkreis weggelassen wurde. Zur Berechnung der Streckenlänge \(~AK~\) wollen wir zunächst die Länge \(~BC=a~\) setzen (denn der Beweis \(~BC=1~\) steht ja noch aus, und auf der Marke sind keine Koordinaten vermerkt) und die Koordinaten \(~(k_1,k_2)~\) von \(~K~\) berechnen. Aus den Gleichungen \(~a+k_1=2 \cdot k_2~\) (Strahlensatz mit \(~AB=2 \cdot BC~\)) und \(~k_1^2+(k_2-a/2)^2=a^2/4~\) erhält man: \[k_1=a \cdot \frac{\sqrt{5}}{5}~~~~~~~~k_2=a \cdot (\frac{1}{2}+ \frac{\sqrt{5}}{10})~~~~~~~~AK=\frac{a}{2} \cdot (1+\sqrt{5})\] Also ist \(~a=1~\) und die Länge \(~AK~\) gleich der Goldenen Zahl.



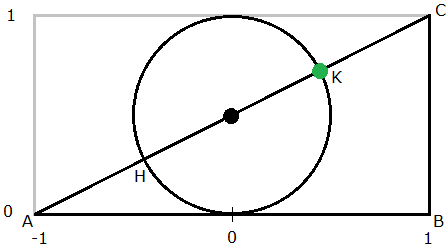
Bild 2

Zum Abschluss wollen wir uns der Skizze über dem Kopf der Schachdame widmen. Sie zeigt ein Pentagramm. Das ist der fünfzackige Stern, der aus dem umgebenden regelmäßigen Fünfeck durch Zeichnung aller Diagonalen entsteht. Das Pentagramm wird überlagert durch einen kleinen Kreis und eine Strecke. Bild 3 zeigt die beiden Bestandteile der Skizze in getrennter Form (mit kleineren Ergänzungen, die noch erklärt werden).


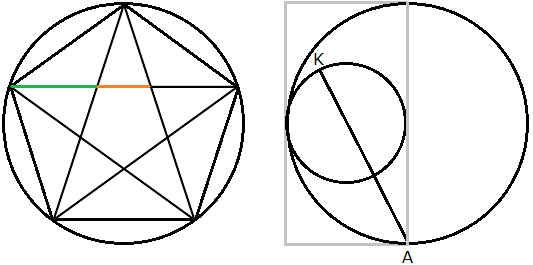
Bild 3

Die rechte Graphik in Bild 3 ist schnell erklärt: Es handelt sich um Bild 2, das um 90° gedreht wurde.  —  Im Pentagramm findet man die Goldene Zahl an mehreren Stellen. Zwei Beispiele: Eine Diagonale hat die \(~\Phi-\)fache Länge einer Fünfeckseite. In Bild 3 stehen die grüne und die orangene Strecke im Verhältnis des Goldenen Schnitts, d.h.  ———:——\(~=\Phi~~\) und  —————:———\(~=\Phi~\).


Südkorea

Südkorea hatte die Ehre, im Weltjahr der Mathematik 2000 die Internationale Mathematik-Olympiade (IMO) auszurichten  —  und streng genommen war die IMO der Anlass für die Ausgabe der Briefmarke, und nicht das WMY.

In den geschweiften Klammern sieht man einige ganze Zahlen und Rechenoperationen, außerdem grüne Rechtecke, ein gelbes rechtwinkliges Dreieck und einen roten Kreis, ferner das Logo der IMO 2000, siehe Bild 4:



Bild 4    Logo der 41. Internationalen Mathematik-Olympiade, Daejeon (Südkorea) 2000

Der blaue Kreis mit der Wellenlinie ist das philosophische Symbol Yin-Yang, das man auch in der Fußzeile der Briefmarke sieht, und das Bestandteil der südkoreanischen Nationalflagge ist. Die Wellenlinie entsteht, indem man zwei Halbkreise mit halbem Radius des Vollkreises an einen Durchmesser des Kreises anlegt, die sich im Mittelpunkt des Vollkreises berühren.



Kategorie: Goldener Schnitt, Goldene Zahl, Fibonacci-Folge

Publiziert 2023-07-13          Stand 2021-03-11