
Italien 2013 Michel 3649 Scott 3199
Geometrische Lehrsätze des Archimedes von Syrakus (287 - 212 v. Chr.)
Mit dieser Briefmarke wurde Archimedes von der italienischen Post 2013 geehrt. Die Unione Matematica Italiana (UMI) hatte anlässlich seines 2300. Geburtstags das Jahr 2013 zum Anno Archimedeo (Archimedisches Jahr) ausgerufen. Da es in unserer Kalenderrechnung kein Jahr 0 gibt, wäre 2014 richtig gewesen, um dieses Jubiläum zu feiern.
Archimedes wurde auf dieser Website bereits mit der Briefmarke # 33 vorgestellt. Die Briefmarke # 125 wurde zum Weltjahr der Mathematik herausgegeben.
Oben rechts auf der Marke steht die Kreiszahl π . Der Hintergrund der Marke zeigt Dezimalstellen von π , aber nicht fortlaufend, sondern mit Lücken bei den Zeilenumbrüchen. In der ersten Zeile ist die 7 am Anfang die 56. und die 2 am Ende die 102. Nachkommastelle; die 6 am Anfang der zweiten Zeile ist die 108. Nachkommastelle; die letzte Ziffer 0 unten rechts ist die 1010. Nachkommastelle.
Die interessantesten Details auf der Marke sind die beiden geometrischen Skizzen. Beide dienen der Beweisführung für Theoreme des Archimedes. - Das obere Bild stammt aus dem ersten Band von Über Kugel und Zylinder. Es illustriert Proposition 21 aus diesem Werk. Dieser Satz ist ein Zwischenergebnis auf dem Weg zur Berechnung der Kugeloberfläche, die Archimedes bereits mit infinitesimalen Methoden durchgeführt hat, etwa 1900 Jahre vor Leibniz und Newton. - Das untere Bild gehört zu Proposition 5 aus dem Buch der Lemmata und steht dort in einer Reihe von Sätzen über die Eigenschaften des Arbelos, einer bestimmten Teilmenge des Kreises. - Wir wollen im Folgenden beide Propositionen beweisen und damit auch die Skizzen auf der Marke erklären.
Über Kugel und Zylinder I, Proposition 21
Proposition 21 ist ein Satz über regelmäßige 2n-Ecke. Im oberen Teil der Marke und in Bild 1 sieht man ein solches Polygon mit seinem Umkreis. Zwei gegenüberliegende Ecken des Polygons ( A und A') werden durch einen Kreisdurchmesser verbunden. Die anderen Ecken sind mit B, C,..., E und B', C',..., E' bezeichnet; dabei sind B und B', C und C' usw. jeweils am Durchmesser AA' gespiegelt, liegen also parallel und jeweils gleich weit von A (und auch A') entfernt.
Für Punkte X, Y soll die Bezeichnung XY sowohl für die Strecke zwischen X und Y als auch für deren Länge verwendet werden, da jeweils aus dem Zusammenhang ersichtlich wird, welches der beiden gemeint ist.
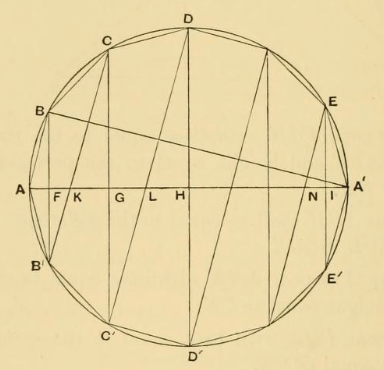
Bild 1
Der Lehrsatz lautet nun:
◊ Proposition 21 im Buch Über Kugel und Zylinder I : (BB' + CC' + ... + EE'):AA' = A'B:AB
Das bedeutet: Die Summe der senkrechten Streckenlängen BB',..., EE' verhält sich zum Durchmesser AA' wie die lange zur kurzen Kathete im Thales-Dreieck mit dem rechten Winkel bei der zu A nächstliegenden Ecke (also B).
In Bild 2 wird das farbig illustriert.
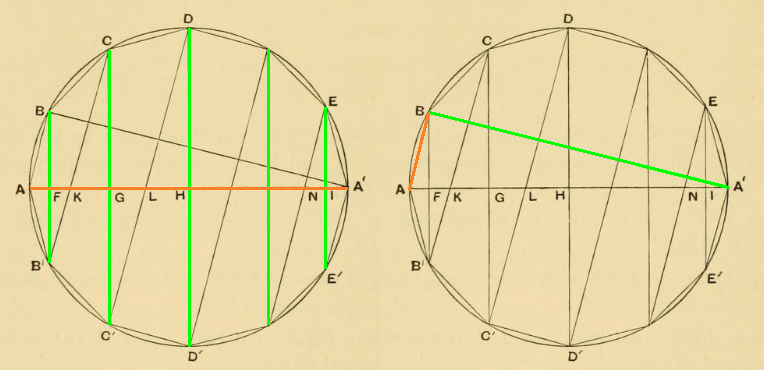
Bild 2
Beweis
In Bild 3 haben alle farbigen Dreiecke die gleichen Winkel an den Ecken des Polygons (Peripheriewinkelsatz), denn diese Winkel sind Peripheriewinkel über den (gleich langen) Kreisbögen zwischen den Polygonecken (der Winkel des orangenen Dreiecks bei B ist der Peripheriewinkel über AB', der Winkel des violetten Dreiecks bei B' ist der Peripheriewinkel über BC usw.). Da außerdem alle farbigen Dreiecke auch rechtwinklig sind, sind sie alle ähnlich. Daraus folgt:
BF:FA = B'F:FK = CG:GK = C'G:GL = DH:HL = ... = EI:IN = E'I:IA'
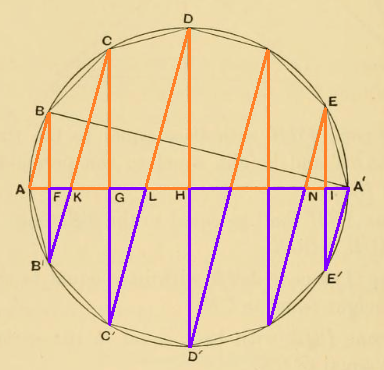
Bild 3
Dann gilt für die Summe der Zähler BF + B'F + ... + E'I = BF + q1·BF + ... + qm·BF = q·BF mit q = 1 + q1 + q2 + ... + qm und m = 2n - 3 ; wegen der eben festgestellten Gleichheit der Brüche gilt für die Summe der Nenner FA + FK + ... + IA' = FA + q1·FA + ... + qm·FA = q·FA . Da in dieser Gleichung die linke Seite gleich AA' ist, erhalten wir (BF + B'F + ... + E'I):AA' = BF:FA . Dies ist gleichbedeutend mit
(BB'+ CC'+ ... + EE'):AA' = BF:FA
Die farbigen Dreiecke in Bild 3 sind aber wegen des Peripheriewinkelsatzes auch ähnlich zum Thales-Dreieck AA'B. Also gilt BF:FA = A'B:AB und damit der Satz. ♦
Buch der Lemmata, Proposition 5
Das Buch der Lemmata enthält drei Theoreme über den Arbelos (griech.: Schustermesser). Diese geometrische Figur entsteht durch Teilung des Durchmessers eines Halbkreises an einem beliebigen Punkt und Errichtung zweier Halbkreise (grün in Bild 4) über den beiden durch die Teilung entstandenen Strecken; der Arbelos ist dann die Restfläche (gelb in Bild 4) im großen Halbkreis bei Wegnahme der kleineren Halbkreise.
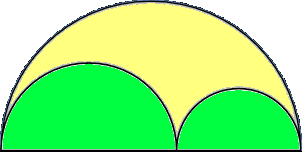
Bild 4
Der Beweis von Proposition 5 verwendet Proposition 1, die wir uns daher zuerst anschauen müssen. Die Skizze dazu sieht man in Bild 5:
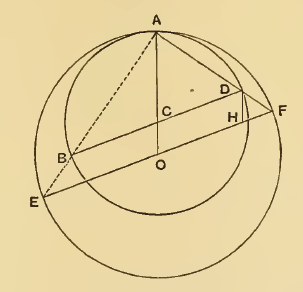
Bild 5
In Bild 5 haben die beiden Kreise den Berührungspunkt A . Durch die beiden Mittelpunkte C (kleiner Kreis) und O sind die parallelen Durchmesser BD und EF gezogen. Die Behauptung lautet:
◊ Proposition 1 im Buch der Lemmata : A, D, F sind kollinear (liegen auf einer Geraden).
Beweis
Zu CO zeichnet man die Parallele DH , mit H auf dem Durchmesser des großen Kreises. Dann gilt OH = CD = CA und OF = OA . Daraus folgt HF = OF-OH = OA-CA = CO = DH . Das kleine Dreieck Δ DHF ist also gleichschenklig; damit gilt für die Winkel: ∠ FDH = ∠ HFD . Das Dreieck Δ ACD ist ebenfalls gleichschenklig; da AC parallel zu DH , und CD parallel zu HF liegt, gilt die Gleichheit der Scheitelwinkel: ∠ DHF = ∠ ACD . Die Dreiecke Δ DHF und Δ ACD sind also ähnlich. Es folgt ∠ CDA + ∠ FDC = ∠ HFD + ∠ FDC = 180° wegen der Parallelität der Durchmesser. Also liegen A, D, F auf einer Geraden. - Die gleiche Argumentation gilt für den Fall, dass einer der Kreise nicht innerhalb, sondern außerhalb des anderen Kreises liegt. ♦
Nun zur Proposition 5, die durch die untere Skizze auf der Briefmarke dargestellt wird. Im Arbelos werden zwei Kreise eingezeichnet; beide berühren den großen Halbkreis und die gemeinsame Tangente der beiden kleinen Halbkreise; außerdem berührt jeder dieser beiden Kreise je einen der beiden kleinen Halbkreise (Bild 6). Dass durch die drei linken und die drei rechten Berührpunkte jeweils genau ein Kreis verläuft, wird im Satz über den Dreiecksumkreis bewiesen - siehe Euklid Elemente Buch IV, Proposition 5.
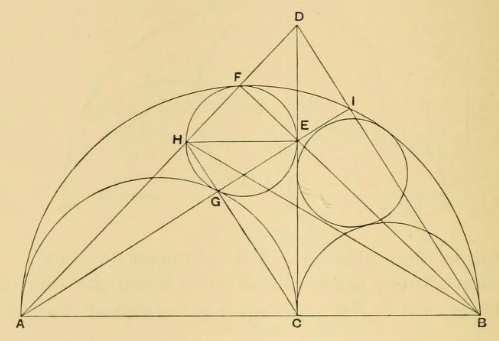
Bild 6
◊ Proposition 5 im Buch der Lemmata : Die beiden Kreise im Arbelos sind gleich groß.
Beweis
Der Beweis bezieht sich nur auf den Durchmesser des linken Kreises im Arbelos - wir werden noch sehen, warum das genügt. Seine Berührpunkte mit der Tangente der kleinen Halbkreise (Fußpunkt C), mit dem großen Halbkreis über AB und dem linken Halbkreis über AC werden mit E, F und G bezeichnet. EH sei derjenige Durchmesser des linken Kreises, der parallel zum Durchmesser AB des großen Halbkreises liegt und somit senkrecht auf CE steht. Nach Proposition 1 sind A, H, F und A, G, E und B, E, F und C, G, H jeweils kollinear. D sei der Schnittpunkt der Geraden durch A, F mit der Geraden durch C, E . I sei der Schnittpunkt der Geraden durch A, E mit dem äußeren, großen Halbkreis über AB . Wir zeigen nun, dass B, I, D kollinear sind. Da Δ ABF als Thalesdreieck rechtwinklig ist, ist E der Höhenschnittpunkt des Dreiecks Δ ABD (Höhen CD und FB ; man beachte: wir wissen noch nicht, dass I auf der Dreiecksseite BD liegt). Also steht die Gerade durch A, E senkrecht auf BD . Da sie nach dem Satz des Thales auch senkrecht auf BI steht, liegt I auf BD , und die Kollinearität von B, I, D ist gezeigt. - Beide Winkel bei G und beide Winkel bei I sind rechte Winkel, somit ist CH parallel zu BD . Deshalb gilt mit zweimaliger Anwendung der Strahlensätze AB:BC = AD:DH = AC:HE . Der Durchmesser des linken Kreises im Arbelos ist also AC·BC:AB . Dieses Ergebnis enthält keinen der Punkte auf dem linken Kreis, sondern nur die drei Punkte auf dem Durchmesser des großen Halbkreises, und ist daher offenbar unabhängig davon, dass wir den linken Kreis im Arbelos gewählt haben; für den rechten Kreis wären im Beweis lediglich die Rollen von A und B zu vertauschen. Also sind die Durchmesser gleich. ♦
Hier sieht man den Ersttagsbrief:

Archimedes-Bilder aus Syrakus