Problem des Monats Februar 2005
Die Lösung steht im unteren Teil der Seite.
Chomp ist ein Spiel für zwei Personen. Es wird auf einem rechteckigen Spielfeld ( n × m - Matrix ) gespielt, das zu Beginn vollständig mit gleichartigen Spielsteinen gefüllt ist:

Bild 1
Bild 1 zeigt eine 4 × 10 - Matrix bei Spielbeginn. Beide Spieler nehmen abwechselnd Steine nach der folgenden Regel weg: Der Spieler am Zug entscheidet sich für einen der noch liegenden Steine (Ankerstein) und nimmt alle Steine weg, die in dem Rechteck liegen, das den Ankerstein als linke untere Ecke hat und das oben und rechts bis zum Spielfeldrand reicht. Als "legale" Spielsituationen entstehen so aus den noch liegenden Steinen "Treppen" von links oben nach rechts unten. Ein typisches Bild zeigt Bild 4 weiter unten. Dies führt zur ersten Frage in diesem Monatsproblem:
Wieviele solcher Treppen gibt es für ein n × m -Chomp-Spiel?
Ausgehend von Bild 1 sind in Bild 2 die beiden ersten Züge eines möglichen Spiels gezeigt. Der Anziehende nimmt die grün dargestellten Steine, der Nachziehende die roten. Die Ankersteine sind invertiert dargestellt.

Bild 2
Derjenige Spieler, der den Stein in der linken unteren Ecke des Spielfelds nimmt, hat verloren.
Überlegen Sie, warum die folgenden Gesetzmäßigkeiten gelten. Die beiden ersten sind ganz einfach:
1.
Liegt noch ein "L" auf dem Feld, also nur Spielsteine in der linken Spalte und der unteren Zeile, so gewinnt der Spieler am Zug genau dann, wenn das "L" verschieden lange Arme hat (siehe Bild 3).
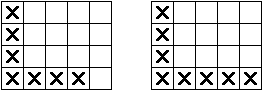
Bild 3
Links: Spieler am Zug verliert. Rechts: Spieler am Zug gewinnt.
2.
Wenn kein "L" auf dem Feld liegt, aber gleich viele Steine (mehr als einer) in der linken Spalte wie in der unteren Zeile liegen, so gewinnt der Spieler, der am Zuge ist (siehe Bild 4). Eine Folge davon ist: Chomp auf quadratischen Spielfeldern ( n = m ) ist uninteressant.

Bild 4
Spieler am Zug gewinnt.
3.
Dies ist schon etwas schwerer: Liegen nur noch zwei gleich lange Zeilen oder zwei gleich lange Spalten von Steinen, so gewinnt der Spieler am Zuge (siehe Bild 5). Also ist Chomp auf zweireihigen Spielfeldern ( 2 × m oder n × 2 ) uninteressant. Die Gewinnstrategie beantwortet auch die allgemeinere Frage, in welchen Fällen der Spieler am Zuge oder sein Gegner bei zwei ungleich langen Zeilen oder Spalten gewinnt.

Bild 5
Spieler am Zug gewinnt.
4.
Es gibt eine Gewinnstrategie für den Anziehenden. Das heißt aber nicht, dass Chomp generell uninteressant wäre. Denn anscheinend kennt bisher niemand diese Strategie. Für genügend große Spielfelder (z.B. 12 × 16 ) hilft es wenig zu wissen, dass der Anziehende theoretisch gewinnt (d.h. wenn er keine Fehler macht).
Die Überlegung, warum es eine Gewinnstrategie für den Anziehenden gibt, ist eigentlich ganz einfach und sofort einsichtig, wenn man sie kennt. Diese Überlegung ist nicht "konstruktiv", d.h. sie beinhaltet nicht die Gewinnstrategie selbst. Da Chomp ein Spiel mit nur endlich vielen möglichen Spielabläufen ist, muss es entweder eine Gewinnstrategie für den Anziehenden oder eine für den Nachziehenden geben. Es reicht also, letzteres zu widerlegen. Wem dies noch nicht reicht, kann sich den Hinweis anschauen.
5.
Für "kleine" n × m -Matrizen ist der gewinnbringende Anfangszug eindeutig bestimmt. Erst beim 8 × 10 -Chomp hat man zwei gewinnbringende Züge für den Anziehenden gefunden. Beweisen Sie, dass für alle zweireihigen und alle quadratischen Chomp-Spiele der gewinnbringende Anfangszug eindeutig ist.
Zum Schluss sollen Sie ein konkretes Spiel analysieren, und zwar das kleinste Chomp-Spiel, das nicht durch die Ergebnisse aus 1.-3. abgedeckt ist:
Bestimmen Sie die Gewinnstrategie des Anziehenden für ein 3 × 4 - Spiel.
Lösung
Zur Notation von Spielständen:
n1 - n2 - ... - nk bezeichnet den Spielstand, bei dem noch k Zeilen liegen, in der untersten Zeile n1 Steine, in der Zeile darüber n2 Steine usw. bis nk Steine in der k-ten Zeile von unten.
Die Notationen für die Bilder 4 und 5 sind also 4-2-2-1 und 8-8.
Zur Notation einzelner Spielsteine:
(i,j) bezeichnet den Stein in der i-ten Zeile von unten und in der j-ten Spalte von links.
Wieviele mögliche Spielsituationen ("Treppen") gibt es für das n × m -Chomp-Spiel?
Es sind n Zeilenlängen aus dem Bereich 0 ... m auszuwählen. Es handelt sich also um ungeordnete Stichproben mit Zurücklegen (Kombinationen mit Wiederholung) von n Elementen aus m + 1 Elementen. Dafür gibt es (n + m)!/(n!·m!) Möglichkeiten. Unter diesen ist allerdings auch das leere Spielfeld. Also gibt es (n + m)!/(n!·m!) - 1 mögliche Spielsituationen. Für das 3 × 4 -Chomp-Spiel sind dies 34 Möglichkeiten, für das 4 × 10 -Chomp-Spiel (Bild 1) 1000 Möglichkeiten.
Ungeordnete Stichproben mit Zurücklegen (Kombinationen mit Wiederholung) liegen also diesem Problem, aber auch den Monatsproblemen Juni 2004 und Oktober 2004 zu Grunde. Der Ausdruck (n + m)!/(n!·m!) beschreibt in den drei Problemen die Anzahl der Möglichkeiten für verschiedene kombinatorische Anordnungen (die sich natürlich ineinander überführen lassen):
- Permutationen von n + m Elementen, von denen je n und m gleich sind
- ungeordnete Stichproben mit Zurücklegen von n aus m + 1 Elementen
- absteigende "Treppen" in einer n × m -Matrix (incl. der "leeren" Treppe)
- kürzeste Wege von links unten nach rechts oben in einem (n + 1) × (m + 1) -Gitter
Zu 1.
Findet der Spieler am Zuge ein "L" mit verschieden langen Armen vor, so nimmt er vom längeren Arm soviele Steine weg, dass ein "L" mit gleich langen Armen entsteht. Sein Gegner muss dann wieder ein "L" mit verschieden langen Armen hinterlassen, so dass sich der Vorgang wiederholt, bis für ihn nur noch der letzte Stein liegen bleibt (falls er nicht schon vorher aufgegeben hat). Entscheidend für diese Gewinnstrategie ist, dass eine einzige Reihe mit mehr als einem Stein eine Gewinnposition für den Spieler am Zug ist und der Spielstand 2-1 eine Verlustposition.
Zu 2.
Dies folgt direkt aus 1., da der Spieler am Zuge als Ankerstein (2,2) nehmen kann und damit ein "L" mit gleich langen Armen hinterlässt.
Zu 3.
Man muss nur den Fall mit zwei Zeilen behandeln, da der Fall mit zwei Spalten symmetrisch dazu liegt und analog behandelt werden kann. Es soll auch gleich der allgemeine Fall n1 - n2 gelöst werden. Durch Ausprobieren erhält man schnell die Erkenntnis, dass für den Spieler am Zuge nur die Spielstände mit n2 = n1 - 1 Verlustpositionen sind. Die Begründung ist ganz ähnlich wie bei 1.: Findet der Spieler am Zuge zwei Zeilen vor, die sich in ihrer Länge nicht um 1 unterscheiden, so kann er genau dies aber für seinen Gegner herstellen; dieser wiederum muss eine Position hinterlassen, bei der sich die Zeilenlängen nicht um 1 unterscheiden. Dieser Vorgang wiederholt sich und endet wie bei 1.
Liegt also ein Rechteck mit zwei Zeilen wie in Bild 5, so nimmt der Spieler am Zuge den oberen rechten Stein weg und gewinnt.
Zu 4.
Der Beweis für die Existenz einer Gewinnstrategie für den Anziehenden bei einem beliebigen Chomp-Spiel gehört in seiner Einfachheit und Eleganz zu den schönsten Beweisen, die ich kenne.
Wenn der Anziehende nur den rechten oberen Stein nimmt, so ist das entweder ein Gewinnzug oder ein Verlustzug. Im ersten Fall ist nichts mehr zu beweisen. Im zweiten Fall gäbe es für den Antwortzug des Nachziehenden einen gewinnbringenden Ankerstein. Aber diesen Ankerstein hätte auch der Anziehende selber im ersten Zug nehmen können!
Zu 5.
Beim zweireihigen Chomp darf der Anziehende nur einen Stein wegnehmen, wenn er gewinnen will. Dies folgt direkt aus 3.
Beim quadratischen Chomp ist der gewinnbringende Ankerstein (2,2) . Dass der Anziehende damit gewinnt, wurde in 2. gezeigt. Andere Anfangszüge führen zum Verlust: Ankersteine aus der unteren Zeile oder der linken Spalte hinterlassen ein Rechteck, so dass 4. zum Tragen kommt. Die übrigen Ankersteine erlauben dem Gegner, selbst den Stein (2,2) zu nehmen, was zu dessen Gewinn führt.
3 × 4 - Chomp
Es gibt nur einen Gewinnzug für den Anziehenden: Er muss den Ankerstein (2,3) nehmen (Bild 6; im folgenden werden die grünen Steine vom Anziehenden und die roten vom Nachziehenden genommen).

Bild 6
Zunächst soll nachgewiesen werden, dass dies tatsächlich ein Gewinnzug ist; danach wird gezeigt, dass es keine weiteren Gewinnzüge für den Anziehenden gibt.
Nimmt der Anziehende den Ankerstein (2,3) wie in Bild 6, so kann der Nachziehende aus acht verschiedenen Ankersteinen auswählen, die aber alle zum Verlust führen:
(1,1) trivial
(1,2) trivial
(1,3) siehe 3.
(1,4) siehe 2.
(2,1) trivial
(2,2) siehe 1.
(3,1) Antwortzug mit Ankerstein (1,4) , siehe 3. (Bild 7 links)
(3,2) Antwortzug mit Ankerstein (1,3) , siehe 3. (Bild 7 rechts)
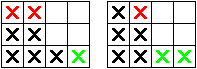
Bild 7
Andere Anfangszüge des Anziehenden scheitern:
(1,1) trivial
(1,2) trivial
(1,3) siehe 3.
(1,4) siehe 2.
(2,1) trivial
(2,2) siehe 1.
(2,4) Antwortzug mit Ankerstein (2,3) (Bild 8 links), führt zum Gewinn des Nachziehenden (siehe Bild 6)
(3,1) siehe 3.
(3,2) Antwortzug mit Ankerstein (1,3) (Bild 8 Mitte), führt nach 3. zum Gewinn des Nachziehenden
(3,3) und (3,4) Antwortzug mit Ankerstein (2,3) (Bild 8 rechts), führt zum Gewinn des Nachziehenden (siehe Bild 6)

Bild 8
Wenn Ihnen das Chomp-Spiel Spaß macht, können Sie weitere Zahlenpaare (n,m) hinsichtlich einer Gewinnstrategie analysieren. Für das nächst-größere Chomp-Spiel (nach den hier behandelten) können Sie den (einzigen) Gewinnzug und einen ergänzenden Hinweis nachlesen: 3 × 5 - Chomp.
Stand 2004-11-11
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite







