Problem des Monats Oktober 2004

Für das Kaffeekränzchen ist jeder Mittwoch Kinotag. Alle acht Damen schauen sich dann gemeinsam einen Film an. Dafür haben sie acht feste Plätze nebeneinander für die Nachmittagsvorstellung reserviert.

Der Operator im Vorführraum und die Platzanweiserin haben nachmittags wenig zu tun. Zum Zeitvertreib schließen sie Wetten ab, z.B. wer von den Damen als erste kommt, wo sie sich hinsetzt usw. Dabei beobachten sie, dass die Damen sehr gesellig sind: Sie kommen zwar alle einzeln an, aber sie lassen beim Hinsetzen keine Lücken. Jede, die neu hinzukommt, setzt sich direkt neben eine andere. Ansonsten können keine Regelmäßigkeiten beobachtet werden, denn die erste Dame, die erscheint, setzt sich zufällig auf irgend einen der acht Plätze, und alle weiteren wählen zufällig einen Platz neben einem der bereits besetzten Plätze aus.

Die Platzanweiserin hat eine Idee und schlägt dem Operator ein "Kaffeekränzchen-Lotto" vor: Es soll für 1 Euro Einsatz darauf gewettet werden, in welcher Reihenfolge die Plätze besetzt werden (also z.B. zuerst Platz 6, dann Platz 7, dann Platz 5 usw.). Die Kassiererin will die Bank spielen und erklärt sich bereit, für einen richtigen Tipp 100 Euro auszuzahlen.

Ist das Angebot der Kassiererin fair?

Lösung

Es gibt eine naheliegende, aber etwas umständliche Lösung, die zuerst angegeben werden soll. Danach wird eine einfache und elegante Lösung präsentiert.


1. Lösungsweg

Wir nummerieren die Plätze von links nach rechts mit  m = 1  bis  m = 8 . Wird der Platz mit der Nr.  m  als erster besetzt, so gibt es  m - 1  freie Plätze links davon und  8 - m  freie Plätze rechts davon. Für die 7 Damen, die nach der ersten eintreffen, gibt es jeweils nur höchstens zwei Möglichkeiten, sich hinzusetzen, die wir mit "L" für links und "R" für rechts von den bereits besetzten Plätzen abkürzen wollen. Also lässt sich das Platznehmen der Damen als 7-tupel mit  m - 1  "L" und  8 - m  "R" darstellen, z.B. für  m = 3 :

(L, R, R, R, L, R, R)

Es ist also die Anzahl aller dieser 7-tupel anzugeben. Dazu bedient man sich kombinatorischer Formeln. Zwei Varianten bieten sich an:

Permutationen (Anordnungen) mit Wiederholung :   7 Elemente in zwei Ausprägungen mit  m - 1  bzw.  8 - m  Elementen lassen sich auf



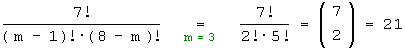
Weisen anordnen.

Kombinationen mit Wiederholung (ungeordnete Stichproben mit Zurücklegen) :   Man schreibt zuerst die  8 - m  "R" nebeneinander und stellt dann die  m - 1  "L" in die Lücken zwischen den "R" bzw. an den linken oder rechten Rand, also an  9 - m  mögliche Plätze. Da auch mehrere "L" in dieselbe Lücke oder an denselben Rand gestellt werden können, handelt es sich um Kombinationen mit Wiederholung, für die es



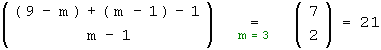
Möglichkeiten gibt.

Für  m = 1, ... , 8  muss man jetzt noch die Binomialkoeffizienten addieren:



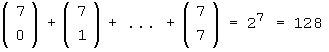
(Begründung: Nach dem binomischen Satz ist die Summe gleich  ( 1 + 1 )⁷ . )

Die drei Angestellten im Kino müssen also bei ihrem "Kaffeekränzchen-Lotto" von  2⁷ = 128  möglichen Reihenfolgen bei der Besetzung der Plätze ausgehen. Im Mittel gewinnen der Operator oder die Platzanweiserin mit jedem 128. abgegebenen Tipp 100 Euro. Die Kassiererin macht also auf lange Sicht einen Gewinn von 21,875 % der Wetteinsätze. Mit etwas Wohlwollen kann man das noch für fair halten.

Die Verallgemeinerung auf  n  Plätze ist jetzt einfach: Wird in einem  n-tupel der  m-te Platz zuerst besetzt, so gibt es  m - 1  freie Plätze links davon und  n - m  freie Plätze rechts davon. Bei den Permutationen kommt man so auf



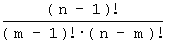
Möglichkeiten. Bei den Kombinationen muss man  m - 1  "L" an  n + 1 - m  Plätze einsortieren; dafür gibt es



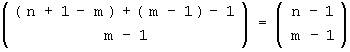
Möglichkeiten; dies entspricht dem Ergebnis, das über die Permutationen gewonnen wurde. Addiert man noch über  m = 1 , ... , n , so erhält man mit dem binomischen Satz:



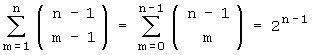
Bei  n  Damen müssten also die drei Angestellten im Kino bei ihrem "Kaffeekränzchen-Lotto" von  2^n-1 möglichen Reihenfolgen für die Besetzung der Plätze ausgehen.



2. Lösungsweg

Es geht auch viel schneller und eleganter, mit einem kleinen Trick: Man lässt den "Film" des Hinsetzens rückwärts laufen. Man würde dann sehen, wie alle Damen nacheinander aufstehen. Jede einzelne von ihnen kann aber nur am linken oder am rechten Rand der noch Sitzenden aufstehen, solange bis nur noch eine einzige sitzt. Also schöpft man bereits alle Möglichkeiten durch eine 7-malige (allgemein:  (n - 1)-malige) Auswahl zwischen links und rechts aus. Dafür gibt es  2⁷ = 128  (allgemein:  2^n-1) Möglichkeiten.



Zu diesem Monatsproblem erreichte mich ein Kommentar von Herrn OStR Heinrich Giebhardt (Johanneum-Gymnasium Herborn), der eine (durchaus plausible) andere Interpretation der Problemstellung enthält; daraus folgt eine wichtige Einschränkung der oben dargestellten Lösung. Ich lasse zunächst Herrn Giebhardt selbst zu Wort kommen:

Wenn die Platzanweiserin "dumm" ist und eine Besetzungsreihenfolge zufällig tippt, ist alles in Ordnung. Aber: Die 128 Möglichkeiten sind nicht gleich wahrscheinlich! Wenn sie also schlau ist und das mit einbezieht, steigen ihre Chancen. Am einfachsten sieht man das bei einem kleinen Beispiel: Nehmen wir an, es sind nur drei Plätze  1,2,3  zu besetzen. Mit je  p = 1/3  ist die Reihenfolge  1,2,3  oder  3,2,1 , aber mit nur je  1/6  2,1,3  und  2,3,1 . Also tippt sie eher darauf, dass ein Randplatz zuerst besetzt wird. Mit anderen Worten: Ihre Lösung setzt eine gleich wahrscheinliche Verteilung voraus. Auch bei  n = 8  besteht für einen zuerst besetzten Randplatz und die dann einzig mögliche Reihenfolge je eine Wahrscheinlichkeit von  1/8 . Also ist es günstig, darauf zu wetten. Dann würde die Platzanweiserin im Mittel 11,50 Euro Gewinn bei 1 Euro Einsatz machen bei 100 Euro Gewinnauszahlung im Fall des richtigen Tipps (Erwartungswert).

Herr Giebhardt hat völlig recht. Ich freue mich, dass es so aufmerksame Problemleser (und -löser) gibt, und danke ihm herzlich.

Bei der von mir vorgestellten Lösung war ich allerdings von anderen Voraussetzungen ausgegegangen. Ich hatte unterstellt, dass es sich wirklich um ein "Kaffeekränzchen-Lotto" handelt, also der Operator und die Platzanweiserin rein zufällig auf eine der 128 Reihenfolgen tippen. Da dies aber aus der Problemstellung nicht eindeutig hervorging, muss die Kassiererin tatsächlich damit rechnen, dass sie mit ihrem Angebot ein schlechtes Geschäft macht.

Man sollte sich  -  für die ursprüngliche Lösung  -  zunächst klarmachen, dass die unterschiedlichen Wahrscheinlichkeiten für die  2^n-1  Möglichkeiten keine Rolle für die Gewinnerwartung spielen, falls die beiden Spieler zufällig eine dieser Möglichkeiten auswählen. Man nummeriert die möglichen Ereignisse von  1  bis  2^n-1  durch und bezeichnet die Wahrscheinlichkeit für das  i-te Ereignis mit  p_i . Die Wahrscheinlichkeit für einen Treffer beträgt  p_i , falls ein Spieler auf das  i-te Ereignis tippt. Auf das  i-te Ereignis wird aber mit Wahrscheinlichkeit  1/2^n-1  getippt, also beträgt insgesamt die Wahrscheinlichkeit für einen Treffer  Σ_i p_i/2^n-1 = 1/2^n-1 .

Falls ein Spieler  -  so wie Heinrich Giebhardt  -  erkennt und ausnutzt, dass die Gewinnwahrscheinlichkeit  1/n  beträgt, falls er darauf tippt, dass als erstes ein Randplatz besetzt wird (und dass die Gewinnwahrscheinlichkeiten für alle anderen Möglichkeiten kleiner sind), so muss die Kassiererin im Mittel  100/n  Euro auszahlen.


Wie sehen die Einzelwahrscheinlichkeiten für die  2^n-1  Möglichkeiten aus? Falls zuerst Platz  1  oder Platz  n  besetzt wird, wurde diese Frage schon beantwortet: Die Wahrscheinlichkeit beträgt  1/n . Die anderen Wahrscheinlichkeiten hängen davon ab, an welcher Stelle der Platzbelegung erstmalig Platz  1  oder Platz  n  auftritt. Diese Stelle soll mit  k  bezeichnet werden.  n - k  ist dann die Anzahl gleichartiger Buchstaben ( L  für links bzw.  R  für rechts) am Anfang der Folge, die sich aus dem 2. Lösungsweg ergibt. Zunächst ein Beispiel mit  n = 8  und  k = 6 :

3-2-4-5-6-1-7-8      R-R-L-R-R-R-L

Bei der ersten Person, die sich hinsetzt, gibt es  n  Möglichkeiten. Danach gibt es solange zwei Möglichkeiten zum Hinsetzen, bis erstmals ein Randplatz, also Platz  1  oder Platz  n  aufgetreten ist. Danach gibt es keine Auswahl mehr, alle übrigen Personen finden nur noch genau einen Platz, auf den sie sich setzen können. Die gesuchte Wahrscheinlichkeit ist also:

1/(n·2^k-1)

Für das Beispiel beträgt diese Wahrscheinlichkeit  1/256 . Die kleinste vorkommende Wahrscheinlichkeit liegt vor, wenn die beiden Randplätze als letzte besetzt werden, nämlich  1/(n·2^n-2) .

Zur "Gegenrechnung" soll die Anzahl der Folgen bestimmt werden, die  1  bzw.  n  (erstmals) an der  k-ten Stelle haben. Für  k = 1  gibt es zwei dieser Folgen. Für  k = 2 ... n - 1  schaut man sich die zugehörige  L/R-Folge an: Nach den  n - k  gleichartigen Buchstaben am Anfang muss zunächst ein anderer Buchstabe stehen (im "rückwärtslaufenden Film" ist das der Zeitpunkt, ab dem beide Randplätze frei sind), die weitere Auswahl  ( k - 2  Buchstaben  L/R )  ist dann beliebig, d.h. es gibt  2^k-2  L/R-Folgen, die mit genau  n - k  "L"  beginnen und genausoviele, die mit genau  n - k  "R"  beginnen. Zusammen sind das  2^k-1  Folgen. Diese Anzahl multipliziert man mit der oben berechneten Wahrscheinlichkeit und summiert über  k  auf; vorangestellt wird das entsprechende Produkt für  k = 1 :

2·¹/n + Σ_k=2..n-1 2^k-1 · ¹/(n·2^k-1) = 2/n + (n-2)/n = 1

Wie erwartet, ist also die Summe der Wahrscheinlichkeiten aller möglichen Ereignisse gleich  1 .



Bemerkung: Die Verwendung von Permutationen bzw. Kombinationen mit Wiederholung lag auch der Lösung des Monatsproblems Juni 2004 zugrunde.