Wieviele Umdrehungen hat das Rad nach einem Umlauf gemacht?
Zur Klärung der Begriffe soll das folgende Bild beitragen (es wurde ein anderer Radius als in der Aufgabenstellung gewählt):
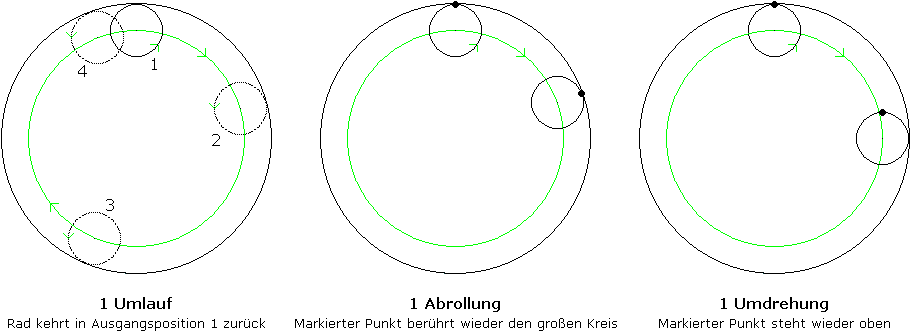
Die zweite Frage:
Wie groß müssen Kreis und Rad sein, damit das Rad bei einem Umlauf genau eine Umdrehung macht?
Die Problemstellung lässt sich verallgemeinern:
Der Kreis soll im Folgenden immer Radius 1 und das Rad Radius r haben. Zwei Fragen sind zu beantworten, und zwar jeweils für ein innen abrollendes Rad ( r < 1 ) und für ein außen abrollendes Rad:
Wieviele Umdrehungen hat das Rad nach einem Umlauf gemacht?
Wieviele volle Umläufe benötigt das Rad, bis es wieder in seiner ursprünglichen Ausrichtung steht?
Zur Verdeutlichung: Markiert man auf der Peripherie des Rades einen Punkt wie in den beiden rechten Bildern oben, so soll nach einer endlichen Anzahl von Umläufen erstmalig das Rad in seiner Ausgangsposition und die Markierung an der selben Stelle stehen.