Seit Oktober 2000 ist das "Problem des Monats" auf meiner Homepage erschienen. Diese ist die 50. und letzte Ausgabe dieser Seite. Ich werde aber weiterhin mathematische Probleme vorstellen, jedoch nicht mehr im Abstand von einem Monat. Aus der Reihe "Problem des Monats" wird die Reihe "Mathematische Probleme", die in größeren und unregelmäßigen Intervallen erscheinen wird.
Problem des Monats März 2005
Die Lösung steht im unteren Teil der Seite.
Ein Rad rollt auf der Innenseite eines Kreises entlang. Der Kreis hat den vierfachen Radius des Rades.
Wieviele Umdrehungen hat das Rad nach einem Umlauf gemacht?
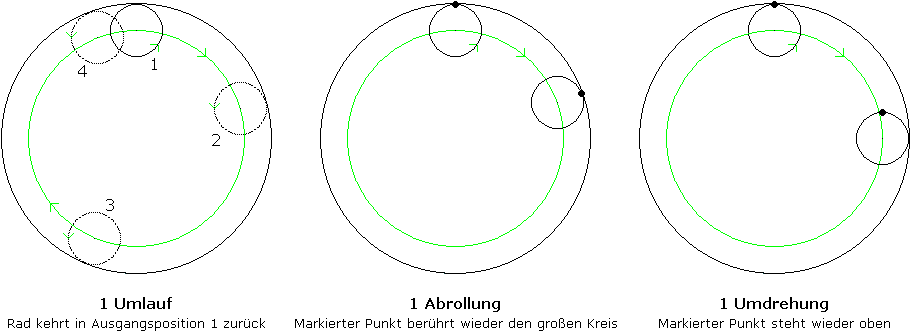
Zur Klärung der Begriffe soll das folgende Bild beitragen (es wurde ein anderer Radius als in der Aufgabenstellung gewählt):
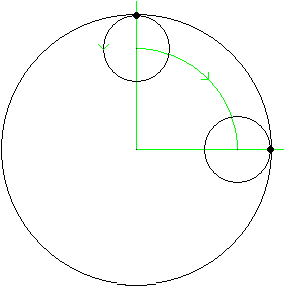
Die zweite Frage:
Wie groß müssen Kreis und Rad sein, damit das Rad bei einem Umlauf genau eine Umdrehung macht?
Die Problemstellung lässt sich verallgemeinern:
Der Kreis soll im Folgenden immer Radius 1 und das Rad Radius r haben. Zwei Fragen sind zu beantworten, und zwar jeweils für ein innen abrollendes Rad ( r < 1 ) und für ein außen abrollendes Rad:
Wieviele Umdrehungen hat das Rad nach einem Umlauf gemacht?
Wieviele volle Umläufe benötigt das Rad, bis es wieder in seiner ursprünglichen Ausrichtung steht?
Zur Verdeutlichung: Markiert man auf der Peripherie des Rades einen Punkt wie in den beiden rechten Bildern oben, so soll nach einer endlichen Anzahl von Umläufen erstmalig das Rad in seiner Ausgangsposition und die Markierung an der selben Stelle stehen.
Lösung
Wieviele Umdrehungen hat ein Rad nach einem Umlauf in einem Kreis mit 4-fachem Radius gemacht?
In der Skizze ist dargestellt, dass eine Abrollung des Rades entlang einem Viertel des Umfangs des großen Kreises erfolgt. Der auf der Peripherie des Rades markierte Punkt ist dann um 270° im Gegenuhrzeigersinn gedreht, also hat das Rad eine 3/4-Umdrehung gemacht. Die Lösung lautet daher:
4 · 3/4 = 3 Umdrehungen
Die zweite Frage (ein Umlauf entspricht einer Umdrehung) kann man zurückstellen, bis weiter unten das allgemeine Problem gelöst ist. Aber man erhält die Lösung auch mit ein wenig Probieren, deshalb soll sie hier schon angegeben werden: Wenn der Kreis den doppelten Radius des Rades hat, entspricht ein Umlauf einer Umdrehung. Denn dann verläuft eine Abrollung entlang einem halben Umfang des großen Kreises ( 1/2 Umlauf), und das Rad hat dann eine halbe Umdrehung gemacht.
Nun wird das allgemeine Problem für das innen laufende Rad gelöst.
In der folgenden Skizze ist eine Abrollung dargestellt:
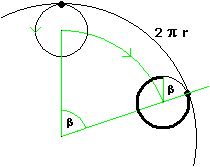
Der Winkel β beträgt im Bogenmaß 2 π r . Der fett eingezeichnete Teil der Radperipherie ist der Weg des markierten Punktes und entspricht einem Winkel von 2 π - β , also (2 π - β) / 2 π = 1 - r Umdrehungen. Andererseits verläuft eine Abrollung auf dem Anteil 2 π r / 2 π = r des Umfangs des großen Kreises.
Ein Umlauf entspricht somit 1/r Abrollungen, also 1/r · (1 - r) = 1/r - 1 Umdrehungen.
Die andere Fragestellung lautete: Wie viele volle Umläufe benötigt das Rad, bis es wieder in seiner ursprünglichen Ausrichtung steht?
In k Umläufen macht das Rad k·(1/r - 1) Umdrehungen. Es ist das kleinste natürliche k gesucht, so dass k·(1/r - 1) eine natürliche Zahl ist. Für irrationale r ist das nicht möglich. Sei also r = p/q rational mit teilerfremden natürlichen Zahlen p, q . Die folgenden Aussagen sind äquivalent:
k·(q/p - 1) ist natürlich.
k·q/p ist natürlich.
k ist ganzzahliges Vielfaches von p .
Für r = p/q benötigt das Rad p Umläufe, bis es wieder in gleicher Position und Ausrichtung steht.
Für irrationale r steht das Rad nach dem 1., 2., ..., n. Umlauf ( n beliebige natürliche Zahl ) in n verschiedenen Ausrichtungen.
Die Tabelle gibt einige Beispiele:
| r |
1/2 |
1/10 |
2/5 |
3/7 |
2/3 |
√1/2 |
| Umdrehungen pro Umlauf |
1 |
9 |
1 1/2 |
1 1/3 |
1/2 |
√2 - 1 |
| Umläufe bis Erreichen der Ausgangslage |
1 |
1 |
2 |
3 |
2 |
- |
Das erste Beispiel in der Tabelle greift noch einmal die zweite Frage von oben auf: Für 1/r - 1 = 1 erhält man r = 1/2 .
Nun zum allgemeinen Problem für das außen laufende Rad.
Hier kann r beliebig groß sein.
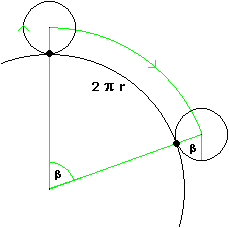
Bei einer Abrollung wie in der Skizze durchläuft der markierte Punkt einen vollen Kreis und zusätzlich den Winkel β , also insgesamt den Winkel (im Bogenmaß) 2 π + β = 2 π + 2 π r ; dies sind 1 + r Umdrehungen. Wie beim innen abrollenden Rad entspricht ein Umlauf 1/r Abrollungen, also hier 1/r + 1 Umdrehungen.
Die Frage nach den vollen Umläufen, die das Rad benötigt, bis es wieder in seiner ursprünglichen Ausrichtung steht, hat die gleiche Antwort und eine analoge Beweisführung wie oben beim innen abrollenden Rad.
Hier sind einige Beispiele für das außen abrollende Rad:
| r |
1 |
1/2 |
2 |
5/3 |
2/11 |
√1/2 |
| Umdrehungen pro Umlauf |
2 |
3 |
1,5 |
1,6 |
6,5 |
√2 + 1 |
| Umläufe bis Erreichen der Ausgangslage |
1 |
1 |
2 |
5 |
2 |
- |
Stand 2005-01-08
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite



