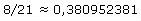
Beispiel 1
| Manfred Börgens Mathematische Probleme # 28 |
Liste aller Probleme mit Lösungen voriges Problem nächstes Problem |
zur Leitseite |
Pingelige Menschen (also auch Mathematiker) wollen immer alles ganz genau wissen. Wenn sie etwa einen Bruch mit dem Taschenrechner als Dezimalzahl ausgeben, also z.B.
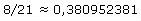
Beispiel 1
dann wüssten sie gerne, wie es hinter der letzten 1 weitergeht. Selbst diese letzte 1 ist nicht sicher, da sie vom Taschenrechner gerundet sein könnte.
Mein Taschenrechner kann 10 Stellen ausgeben, so wie in Beispiel 1. Deshalb werden auch alle weiteren Rechnungen so dargestellt. Bei manchen Brüchen ahnt man (oder weiß man), wie das vollständige Ergebnis lautet:
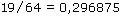
Beispiel 2
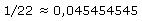
Beispiel 3a
In Beispiel 2 erhält man eine abbrechende Dezimalzahl, und alle Dezimalstellen werden auch ausgegeben; in Beispiel 3a erhält man eine periodische Dezimalzahl:
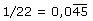
Beispiel 3b
Die Hauptfrage dieses Monatsproblems lautet:
Für welche Brüche kann man auf dem Taschenrechner die vollständige Dezimalentwicklung ablesen?
Diese Frage soll später noch präzisiert werden.
Es reicht offenbar aus, nur positive und maximal gekürzte Brüche zu betrachten, die zudem kleiner als 1 sind, d.h. a / b mit a, b teilerfremde natürliche Zahlen und a < b .
Jeder dieser Brüche hat in seiner Dezimaldarstellung einen nichtperiodischen Abschnitt hinter dem Komma mit der Vorperiodenlänge h und dahinter einen periodischen Teil mit der Periodenlänge j. In Beispiel 3b ist h = 1 und j = 2. Ist h = 0 , so ist a / b eine reinperiodische Dezimalzahl, ist j = 0, so ist a / b eine abbrechende Dezimalzahl. Alle anderen Brüche heißen gemischtperiodisch.
Eine vorbereitende Aufgabe in diesem Monatsproblem ist es, anhand von Beispielen einen Satz darüber zu formulieren, wie h und j aus a / b bestimmt werden können:
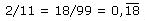
Beispiel 4
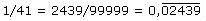
Beispiel 5a
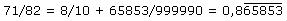
Beispiel 5b
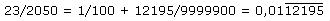
Beispiel 5c
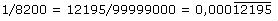
Beispiel 5d
Man vergleiche in den Beispielen 5a-d die Nenner! Welche Vermutung ergibt sich daraus für die Vorperiodenlänge? (Für eine kleine Hilfestellung finden Sie hier Hinweis 1.) Die Brüche sind in den Beispielen 4 und 5a-d jeweils im ersten Schritt umgewandelt worden, um eine Vermutung für die Periodenlänge zu erleichtern. (Für eine kleine Hilfestellung finden Sie hier Hinweis 2.) Welchen Einfluss hat der Zähler auf Vorperiodenlänge und Periodenlänge? Rechnen Sie selbst weitere Beispiele! So erhalten Sie die Antwort auf die folgende Frage:
Welche Vorperiodenlänge und welche Periodenlänge hat a / b ?
Frage 1
(Sie können hier den entsprechenden Lehrsatz nachlesen, um Ihre Vermutung zu überprüfen und ein weiteres Beispiel zu sehen.)
Nun zurück zur Ausgangsfrage. Wenn Vorperiodenlänge oder Periodenlänge zu groß sind, passen nicht alle relevanten Dezimalstellen auf ein Taschenrechnerdisplay. Aber welche Brüche erlauben eine vollständige Darstellung, wenn nur 10 Ziffern zur Verfügung stehen?
Zunächst sollte man darauf achten, keine Dezimalstellen zu verschenken:
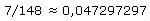
Beispiel 6a
Die Taschenrechnerausgabe in Beispiel 6a lässt sich verbessern, indem man z.B. mit 10 11 multipliziert:
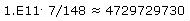
Beispiel 6b
Dies soll zeigen, dass man durch geeignete Multiplikation mit einer Zehnerpotenz immer alle 10 Stellen des Taschenrechners ausnutzen kann. Aber Vorsicht: Die letzten beiden Stellen sind gerundet. Diese Rundung lässt sich erkennen, wenn man vorher ermittelt hat, dass die Vorperiodenlänge 2 und die Periodenlänge 3 ist.
Nun lässt sich die Ausgangsfrage konkretisieren:
Für welche Nenner b ist für alle Zähler a der Bruch a / b eine abbrechende Dezimalzahl und vollständig mit dem Taschenrechner darstellbar? Wie viele solcher Nenner gibt es?
Frage 2
Für welche Nenner b ist für alle Zähler a der Bruch a / b eine reinperiodische Dezimalzahl und vollständig mit dem Taschenrechner darstellbar? Wie viele solcher Nenner gibt es?
Frage 3
Für welche Nenner b ist für alle Zähler a der Bruch a / b eine gemischtperiodische Dezimalzahl und vollständig mit dem Taschenrechner darstellbar? Wie viele solcher Nenner gibt es?
Frage 4
Wie stellt man allgemein für einen Bruch a / b fest, ob und wie er vollständig mit dem Taschenrechner als Dezimalzahl darstellbar ist? Gegenüber Fragen 2-4 erhält man noch weitere Nenner, wenn a klein genug ist.
Frage 5
Welche sind die kleinsten Nenner, für die der Taschenrechner nicht mehr für alle Zähler ein vollständiges Ergebnis ausgeben kann?
Frage 6
Welche sind die kleinsten Nenner, für die der Taschenrechner nicht mehr für irgendeinen Zähler ein vollständiges Ergebnis ausgeben kann?
Frage 7
Zur Geschichte der Dezimaldarstellung
Kategorie: Zahlen und Zahlsysteme, Berechnung von π