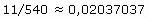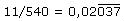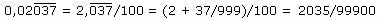Welche Vorperiodenlänge und welche Periodenlänge hat  a / b ?

Entscheidend ist nur der Nenner  b. Durch eine Primfaktorzerlegung lässt sich ermitteln, mit welchen Potenzen (q  bzw. r)  b  die Faktoren  2  und  5  enthält.

Satz:
Ist  b = 2 ^q · 5 ^r · b ₁  (b ₁ nicht durch  2  oder  5  teilbar), so hat  a / b  die Vorperiodenlänge  h = max { q , r }. Falls  b ₁ > 1  ist, ist die Periodenlänge  j  das kleinste natürliche  k, für das  b ₁  ein Teiler von  10 ^k - 1  ist.

Man erhält also genau dann eine abbrechende Dezimalzahl, wenn in der Primfaktorzerlegung von  b  nur 2en und 5en auftreten (dann ist  b ₁ = 1). Man erhält eine reinperiodische Dezimalzahl, falls  b  nicht durch  2  und nicht durch  5  teilbar ist (dann ist  q = r = 0). Die Periodenlänge von rein- und gemischtperiodischen Brüchen entspricht der Stellenzahl der kleinsten Zahl unter  9, 99, 999, ..., die  b ₁  als Teiler hat. Der Zähler  a  spielt dabei keine Rolle.

Ein Beispiel:  11 / 540  hat  2  nichtperiodische Stellen hinter dem Komma und dahinter eine Periode der Länge  3. Denn  540 = 2² · 5 · 27 , und  27  teilt nicht  9  oder  99, aber  999. Hier ist das Taschenrechnerergebnis und die vollständige Darstellung:




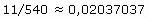
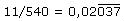
Anhand dieses Beispiels lässt sich auch gut zeigen, wie man umgekehrt aus einer periodischen Dezimalzahl den zugehörigen Bruch konstruiert:



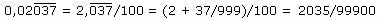
Die Anzahl der Neunen im Nenner ist gleich der Periodenlänge, die der Nullen gleich der Länge des nichtperiodischen Teils. Nach Kürzen des letzten Bruches erhält man wieder  11 / 540.

Manfred Börgens - Problem des Monats März 2003 - Lehrsatz - Stand 26.8.2003

zum Monatsproblem     zur Lösung               zur Leitseite