Manfred Boergens - Problem 95 mit Loesung

Manfred Börgens
Mathematische Probleme # 95

Liste aller Probleme mit Lösungen
voriges Problem nächstes Problem

Sphärische Triangulation

Teil 4 Teil 1 Teil 2 Teil 3

Die Lösung steht im unteren Teil der Seite.

In den ersten drei Teilen der "Sphärischen Triangulation" wurden Kugel-Deltaeder vorgestellt, also konvexe Polyeder, deren sämtliche Flächen Dreiecke sind und deren Ecken alle auf der Umkugel liegen. Diese ermöglichen eine Triangulation der Kugel, da die Kanten der Polyeder durch die entsprechenden Geodätischen auf der Kugel ersetzt werden können.

In diesem vierten Teil sollen nur spezielle Kugel-Deltaeder behandelt werden, die wir Kuppel-Deltaeder nennen wollen, da sie beim Bau Geodätischer Kuppeln bevorzugt verwendet werden. Ein Kuppel-Deltaeder ist ein Kugel-Deltaeder, an dessen sämtlichen Ecken 5 oder 6 Kanten (bzw. Dreiecke) zusammentreffen.

Was wissen wir aus den ersten drei Teilen der "Sphärischen Triangulation" über konvexe Polyeder, die nur von Dreiecken begrenzt werden? F soll die Anzahl der Flächen bezeichnen, E die Anzahl der Ecken und K die Anzahl der Kanten.

Deltaedersatz: K = F·(3/2) und E = F/2 + 2 . F ist gerade.

Für alle geraden F ≥ 4 gibt es ein Kugel-Deltaeder.

Die einzigen regulären Kugel-Deltaeder sind die Platonischen Körper Tetraeder, Oktaeder und Ikosaeder.

Bezeichnet in einem Kuppel-Deltaeder E₅ die Anzahl der Ecken mit 5 Kanten und E₆ die Anzahl der Ecken mit 6 Kanten, so gilt E₅ = 12 und E₆ = F/2 - 10 .

Drei Kuppel-Deltaeder wurden beschrieben: Ikosaeder (E₆ = 0), Penta-Dodekaeder (E₆ = 20) und Tetra-Ikosaeder (E₆ = 30).

Aufgabe:
Finden und beschreiben Sie weitere Kuppel-Deltaeder.

Vorschlag:

Man sucht zunächst möglichst einfache Grundformen von Kuppel-Deltaedern. Davon kennen wir bereits zwei - Ikosaeder und Penta-Dodekaeder - , aber es gibt noch mehr dieser "Kuppel-Deltaeder 1. Ordnung".

Aufbauend auf diesen kann man leicht (unendlich viele) weitere Kuppel-Deltaeder bilden, indem man die Flächen (Dreiecke) in kleinere Dreiecke unterteilt; so erhält man "Kuppel-Deltaeder 2. Ordnung". Dabei ist darauf zu achten, dass an den neu entstehenden Ecken wieder 5 oder 6 Kanten zusammentreffen. Als Vorbild dafür dient das Tetra-Ikosaeder. Dort wurde jede Fläche in 4 Dreiecke unterteilt. Wenn man die Kanten statt in 2 in j Stücke teilt, erhält man j² Teildreiecke. Das lässt sich bei allen Kuppel-Deltaedern 1. Ordnung für j ≥ 2 durchführen.

Zurück zum ersten Punkt: Da man für die Kuppel-Deltaeder 1. Ordnung eine Umkugel benötigt, nimmt man sich am besten zuerst die Archimedischen Körper vor. Unter diesen kommen zwar keine Kuppel-Deltaeder vor (sonst wären es ja Platonische Körper), aber die Konstruktion des Penta-Dodekaeders in Teil 2 zeigt auf, wie man auch aus Archimedischen Körpern Kuppel-Deltaeder herstellen kann.

Dann kann man noch nach weiteren Polyedern (oder ganzen Polyeder-Klassen) forschen, die für die Konstruktion von Kuppel-Deltaedern in Frage kommen.

Hilfreiche und schöne Web-Quelle: Werner Brefeld: Geodätische Kuppeln

Lösung

Hier sind wichtige Klassen von Polyedern, die eine Umkugel aufweisen: Platonische Körper, Archimedische Körper, Prismen, Antiprismen.

Welche Polyeder aus diesen Klassen sind Kuppel-Deltaeder?

Da an jeder Ecke 5 oder 6 Kanten zusammentreffen müssen, ist unter den Platonischen Körpern nur das Ikosaeder ein Kuppel-Deltaeder.

Unter den Archimedischen Körpern und den Prismen kommen keine Kuppel-Deltaeder vor, da alle Flächen Dreiecke sein müssen.

Es gibt ein Antiprisma, das nur aus Dreiecken besteht, nämlich das Oktaeder, aber das wird schon unter den Platonischen Körpern aufgeführt; außerdem treffen an jeder Ecke nur 4 Kanten zusammen.

Als nächstes schauen wir, ob sich in den genannten Klassen Polyeder finden lassen, die sich analog zum Penta-Dodekaeder in Teil 2 zu Kuppel-Deltaedern 1. Ordnung ausgestalten lassen. Dafür kommen diejenigen Polyeder in Frage, die Fünfecke oder Sechsecke als Flächen haben, denn diese lassen sich in 5 oder 6 Dreiecke teilen. Dann müssen aber die anderen Flächen des Ursprungskörpers Dreiecke sein, und nach der Teilung muss wieder die Forderung nach 5 oder 6 Kanten an jeder Ecke überprüft werden.

Wir werden dafür eine einheitliche Terminologie brauchen. Wenn also ein Polyeder mit Umkugel nur aus Dreiecken, Fünfecken oder Sechsecken besteht, so soll das Polyeder, das durch Teilung der Fünfecke und Sechsecke mit anschließender Ausziehung (Projektion) der neuen Ecken auf die Umkugel entsteht, durch ein vorgestelltes "Tri-" bezeichnet werden (das soll an die Triangulation erinnern). Wir werden also ab hier das Penta-Dodekaeder mit Tri-Dodekaeder benennen. Offenbar ist das Tri-Dodekaeder der einzige Platonische Körper, bei dem dieses Verfahren möglich ist.

Die Archimedischen Körper erweisen sich Fundgrube für Polyeder, die sich zu Kuppel-Deltaedern umgestalten lassen. Wir suchen also unter den Archimedischen Körpern diejenigen, die nur Dreiecke, Fünfecke und Sechsecke als Flächen aufweisen.

Wir finden vier Kandidaten:

Tetraederstumpf (4 Dreiecke, 4 Sechsecke)

Ikosidodekaeder (20 Dreiecke, 12 Fünfecke)

Ikosaederstumpf (12 Fünfecke, 20 Sechsecke)

Abgeschrägtes Dodekaeder (80 Dreiecke, 12 Fünfecke)

Unter den Antiprismen findet sich ebenfalls ein Kandidat:

Hexa-Antiprisma (12 Dreiecke, 2 Sechsecke)

Bei allen fünf Kandidaten wird sich herausstellen, dass nach der Triangulierung - also nach der Teilung aller Fünf- und Sechsecke in Dreiecke - Kuppel-Deltaeder entstehen, so dass fünf weitere Kuppel-Deltaeder 1. Ordnung hinzukommen (insgesamt kennen wir dann sieben von ihnen); hier sind sie der Größe nach geordnet:

Tri-Hexa-Antiprisma

Tri-Tetraederstumpf

Tri-Ikosidodekaeder

Tri-Abschräg-Dodekaeder

Tri-Ikosaederstumpf

Unter den gefundenen sieben Kuppel-Deltaedern 1. Ordnung ist somit ein Platonischer Körper, ein triangulierter Platonischer Körper, ein trianguliertes Antiprisma und vier triangulierte Archimedische Körper.

Hier ist ein erster überblick über diese Polyeder. Danach folgt eine genauere Untersuchung.

	Dodekaeder	Hexa-Antiprisma	Tetraederstumpf	Ikosidodekaeder	Ikosaederstumpf	Abschräg-Dodekaeder


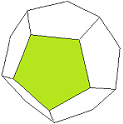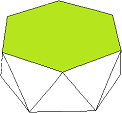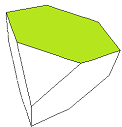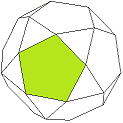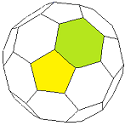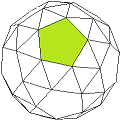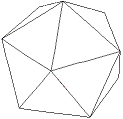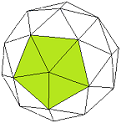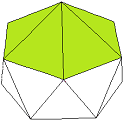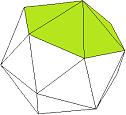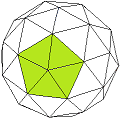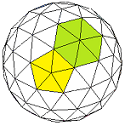Ikosaeder	Tri-Dodekaeder	Tri-Hexa-Antiprisma	Tri-Tetraederstumpf	Tri-Ikosidodekaeder	Tri-Ikosaederstumpf	Tri-Abschräg-Dodekaeder

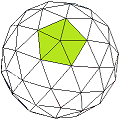
Die sieben Kuppel-Deltaeder 1. Ordnung stehen unten, jeweils unter ihren nicht-triangulierten Ursprungskörpern. Man kann an den unteren Bildern gut erkennen, dass - wie gefordert - an jeder Ecke fünf oder sechs Kanten zusammentreffen.

Aus allen Kuppel-Deltaedern lassen sich natürlich topologisch gleichartige herstellen, indem man die Ecken auf der Kugel leicht verrückt. Diese wollen wir nicht als neue oder zusätzliche Kuppel-Deltaeder auffassen. Hier kommt es auf die Anzahl F der Flächen (Dreiecke) an (daraus lassen sich E, E₆ und K berechnen).

Nun sollen Kuppel-Deltaeder genauer beschrieben und nach der Anzahl der Dreiecke F geordnet werden. Ein Kuppel-Deltaeder 2. Ordnung geht aus einem Kuppel-Deltaeder 1. Ordnung durch Teilung aller Dreiecke in jeweils j² Dreiecke hervor; dabei werden alle Kanten der Kuppel-Deltaeder in jeweils j gleiche Stücke geteilt. Die neu entstehenden Ecken werden auf die Umkugel projiziert. Für j = 2 kennen wir dieses Verfahren bereits für das Tetra-Ikosaeder (siehe Teil 1). Das nächste Bild zeigt die Teilung und Projektion für j = 3 ; für größere j geht man analog vor.

j_3

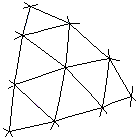
Wir wollen eine einheitliche Terminologie für Kuppel-Deltaeder 2. Ordnung vereinbaren. Durch das eben beschriebene Teilungsverfahren wird die Anzahl der Dreiecke mit dem Faktor j² vervielfacht. Deshalb soll j²- als Präfix vor den Namen des Kuppel-Deltaeders 1. Ordnung gestellt werden. Dadurch wird das Tetra-Ikosaeder zum 2²-Ikosaeder.

Die bisher beschriebenen Kuppel-Deltaeder werden nun bis F ≤ 200 genauer dargestellt, nach F geordnet. Links sind die Polyeder vor und rechts nach der Triangulation abgebildet. Die Formel für die Ecken hat die Gestalt E = E₅ + E₆ = 12 + E₆ .

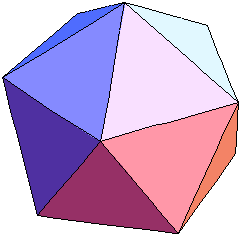
Bild 1 Ikosaeder → 1. Ordnung F = 20 E = 12 + 0

Das Ikosaeder ist der einzige Platonische Körper unter den Kuppel-Deltaedern. Alle anderen Kuppel-Deltaeder weisen also auch nicht-gleichseitige Dreiecke auf, sind also nicht regulär wie Platonische und Archimedische Körper und (Anti-)Prismen.

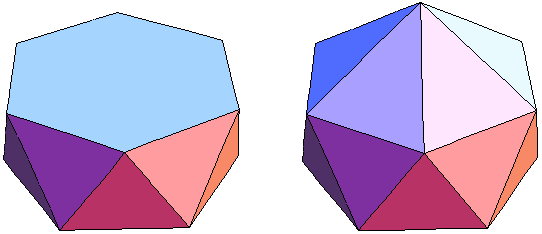
Bild 2 Hexa-Antiprisma und Tri-Hexa-Antiprisma → 1. Ordnung F = 24 E = 12 + 2

Unter den Antiprismen kommen für die Umformung zu Kuppel-Deltaedern nur das Penta-Antiprisma (2 Fünfecke, 10 Dreiecke) und das Hexa-Antiprisma (2 Sechsecke, 12 Dreiecke) in Frage. Das Tri-Penta-Antiprisma ist aber identisch mit dem Ikosaeder.

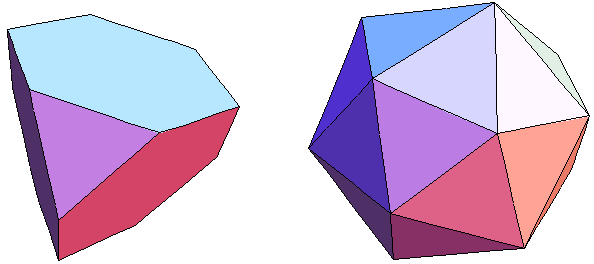
Bild 3 Tetraederstumpf und Tri-Tetraederstumpf → 1. Ordnung F = 28 E = 12 + 4

Der Tetraederstumpf entsteht aus dem Tetraeder durch Abschneiden aller 4 Ecken bis jeweils zum Drittel der Kantenlängen. Die 4 Schnittflächen sind dann gleichseitige Dreiecke, und aus den ursprünglichen Dreiecksseiten des Tetraeders werden 4 gleichseitige Sechsecke. Bei der Umformung zum Tri-Tetraederstumpf bleiben die Dreiecke erhalten, und aus den Sechsecken werden insgesamt 24 Dreiecke, die durch die Projektion der 4 neu entstandenen Ecken auf die Umkugel nur noch gleischenklig, aber nicht mehr gleichseitig sind.

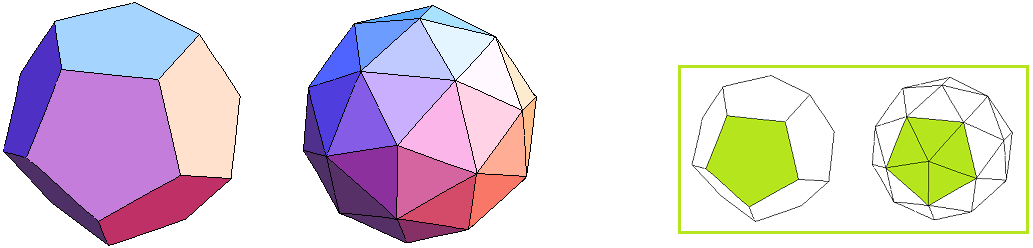
Bild 4 Dodekaeder und Tri-Dodekaeder → 1. Ordnung F = 60 E = 12 + 20

Wir sehen hier das einzige Kuppel-Deltaeder 1. Ordnung, das durch Triangulierung eines Platonischen Körpers entsteht. Das Tri-Dodekaeder wurde unter dem Namen Penta-Dodekaeder ausführlich in Teil 2 und Teil 3 untersucht.

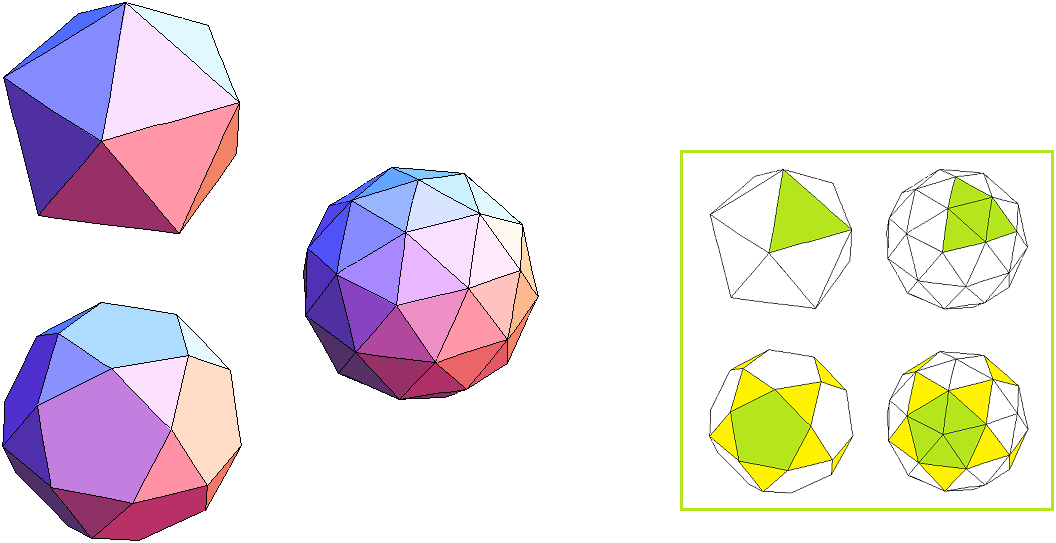
Bild 5 Ikosaeder, Ikosidodekaeder und 2²-Ikosaeder = Tri-Ikosidodekaeder → 1. Ordnung und 2. Ordnung (j = 2) F = 80 E = 12 + 30

Hier taucht ein interessantes Phänomen auf: Das Kuppel-Deltaeder lässt sich auf zwei verschiedene Weisen herstellen. Das in Bild 5 links unten abgebildete Ikosidodekaeder ist ein Archimedischer Körper mit 20 Dreiecken und 12 Fünfecken. Es entsteht, wenn man von einem Ikosaeder alle 12 Ecken abschneidet (dadurch entstehen die Fünfecke); die Schnitte verlaufen durch die Kantenmitten des Ikosaeders, so dass von den ursprünglichen 20 Dreiecken jeweils die kleinen Mitteldreiecke stehen bleiben. Durch Triangulierung der 12 Fünfecke zu 60 Dreiecken und Projektion der Fünfeckmitten auf die Umkugel entsteht das Tri-Ikosidodekaeder.

Es gibt aber auch einen anderen (vielleicht einfacheren) Weg, um dieses Kuppel-Deltaeder herzustellen. Teilt man alle 20 Flächen des Ikosaeders (links oben) in 4 kleinere Dreiecke (mit anschließender Projektion der neuen Ecken auf die Umkugel), erhält man ebenfalls ein Kuppel-Deltaeder mit F = 80 (siehe Teil 1 und Teil 3).

Dass aus beiden Körpern das gleiche Kuppel-Deltaeder entsteht, sieht am besten an der folgenden Graphik:

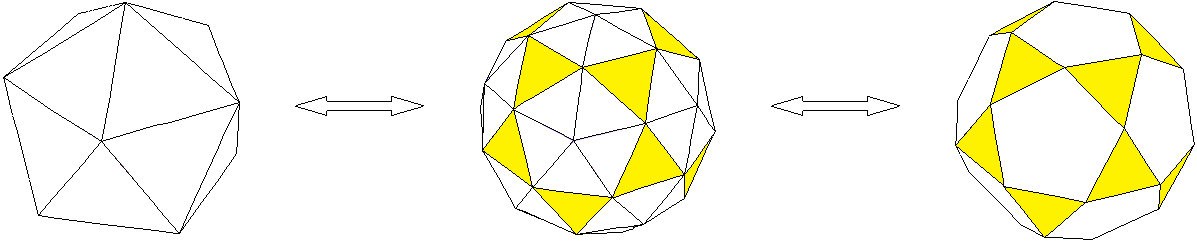
Aequivalenz_1

Man geht aus vom Ikosaeder und macht die 2²-Teilung (erstes Bild  →  zweites Bild), um das Kuppel-Deltaeder zu erhalten. Es entstehen 12 "E₅-Ecken" (dort treffen 5 weiße Dreiecke zusammen). Fasst man jeweils 5 weiße Dreiecke zu einem Fünfeck zusammen, so grenzen an den Kanten dieser weißen Fünfecke Dreiecke (gelb) an, mit der Abfolge "5-3-5-3" an den weiß/gelben Ecken.

Diese weißen Fünfecke ebnet man ein (zweites Bild  →  drittes Bild). Es bleiben 12 gleichseitige Fünfecke und die Mitteldreiecke aus der 2²-Teilung übrig, mit der Abfolge "5-3-5-3" an allen Ecken, also erhält man ein Ikosidodekaeder.

Alle Schritte sind umkehrbar; alle drei Körper haben die gleiche Umkugel.

Also ist ein 2²-Ikosaeder auch ein Tri-Ikosidodekaeder.

Vorsicht: Stellt man aus einem Ikosaeder ein Ikosidodekaeder her (durch Abschneiden der Ecken auf der Hälfte der Kanten), so ist dies nicht der rechte Körper, denn es wird zunächst die Umkugel kleiner. Also wären dann auch die Dreiecke auf dem Ikosidodekaeder kleiner als die Mitteldreiecke des 2²-Ikosaeders (drittes Bild  →  zweites Bild). Will man also vom Ikosaeder über das Ikosidodekaeder zum Kuppel-Deltaeder kommen, schneidet man erst die Ecken des Ikosaeders ab, teilt dann die Fünfecke des so entstandenen Ikosidodekaeders in jeweils 5 Dreiecke und projiziert die Mittelpunkte der Fünfecke auf die Ikosidodekaeder-Umkugel. Schließlich vergrößert man den ganzen Körper, indem alle Ecken auf die Kugel mit gleichem Mittelpunkt und Radius 1 projiziert werden.

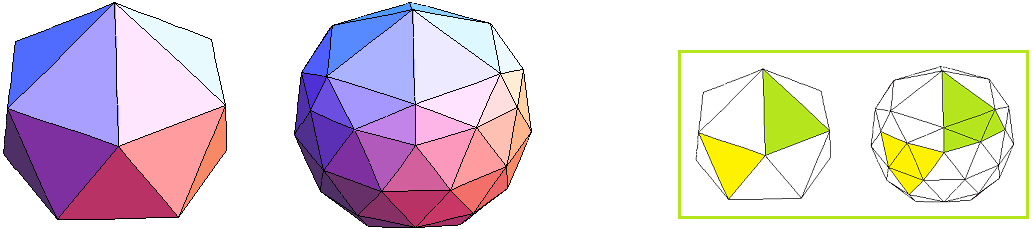
Bild 6 Tri-Hexa-Antiprisma und 2²-Tri-Hexa-Antiprisma → 2. Ordnung (j = 2) F = 96 E = 12 + 38

Das Tri-Hexa-Antiprisma kam schon als Kuppel-Deltaeder 1. Ordnung vor (Bild 2). Im kleinen, grün umrundeten Bild sieht man, dass die MATHEMATICA-Graphik die gelben Dreiecke gleichmäßiger teilt als die grünen; das ließe sich natürlich leicht ändern.

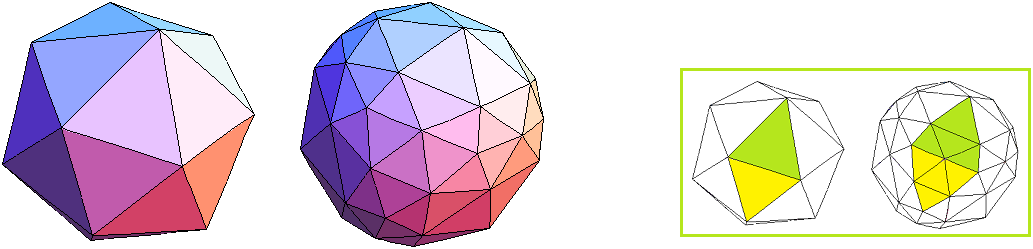
Bild 7 Tri-Tetraederstumpf und 2²-Tri-Tetraederstumpf → 2. Ordnung (j = 2) F = 112 E = 12 + 46

Der Tri-Tetraederstumpf kam schon als Kuppel-Deltaeder 1. Ordnung vor (Bild 3). Im kleinen, grün umrundeten Bild sieht man, dass die MATHEMATICA-Graphik die gelben Dreiecke gleichmäßiger teilt als die grünen; das ließe sich natürlich leicht ändern.

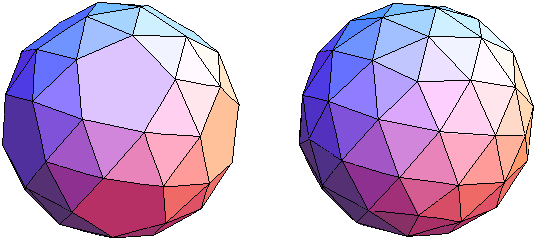
Bild 8 Abgeschrägtes Dodekaeder und Tri-Abschräg-Dodekaeder → 1. Ordnung F = 140 E = 12 + 60

Das abgeschrägte Dodekaeder ist einer der am schwierigsten herzustellenden Archimedischen Körper. Man kann es aus einem Dodekaeder nicht durch einfaches Abschneiden von Ecken erzeugen. Es hat als Flächen 80 Dreiecke und 12 Fünfecke, woraus sofort F = 140 und damit E₆ = 60 folgt.

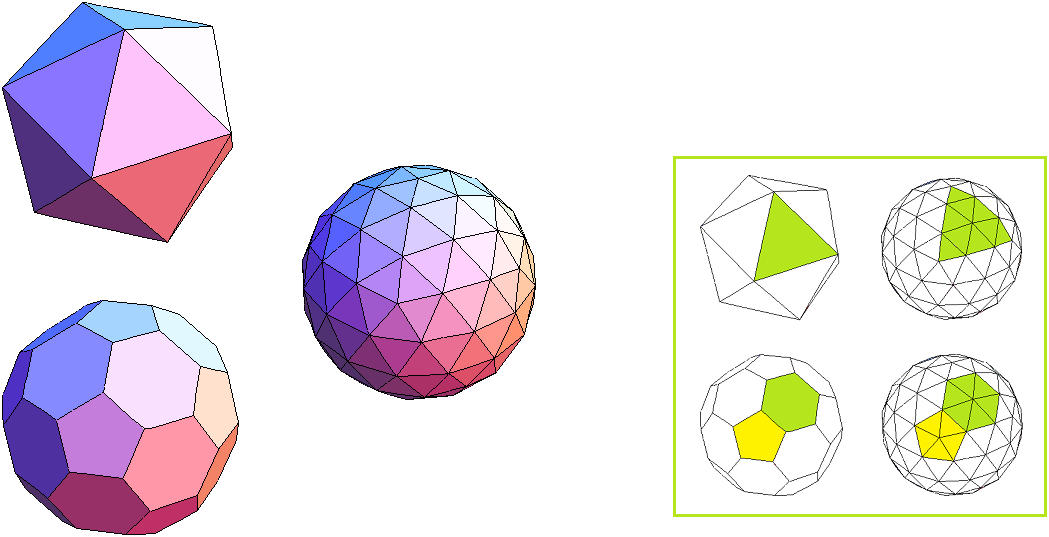
Bild 9 Ikosaeder, Ikosaederstumpf und 3²-Ikosaeder = Tri-Ikosaederstumpf → 1. Ordnung und 2. Ordnung (j = 3) F = 180 E = 12 + 80

Auch hier (wie in Bild 5) stoßen wir auf ein Kuppel-Deltaeder, das sich auf zwei verschiedene Weisen herstellen lässt. Links unten in Bild 9 sehen wir den Ikosaederstumpf, einen Archimedischen Körper mit 12 Fünfecken und 20 Sechsecken als Flächen. Er entsteht, wenn man von einem Ikosaeder alle 12 Ecken abschneidet (dadurch entstehen die 12 Fünfecke); die Schnitte verlaufen durch die gedrittelten Kanten des Ikosaeders, so dass aus den ursprünglichen 20 Dreiecken 20 Sechsecke entstehen. Durch Triangulierung der 12 Fünfecke zu 60 Dreiecken und der 20 Sechsecke zu 120 Dreiecken sowie der Projektion der Fünfeck- und Sechseckmitten auf die Umkugel entsteht der Tri-Ikosaederstumpf.

Es gibt aber auch einen anderen (vielleicht einfacheren) Weg, um dieses Kuppel-Deltaeder herzustellen. Teilt man alle 20 Flächen des Ikosaeders (links oben in Bild 9) in 9 kleinere Dreiecke (mit anschließender Projektion der neuen Ecken auf die Umkugel), erhält man ebenfalls ein Kuppel-Deltaeder mit F = 180 .

Dass aus beiden Körpern das gleiche Kuppel-Deltaeder entsteht, sieht man am besten an der folgenden Graphik:

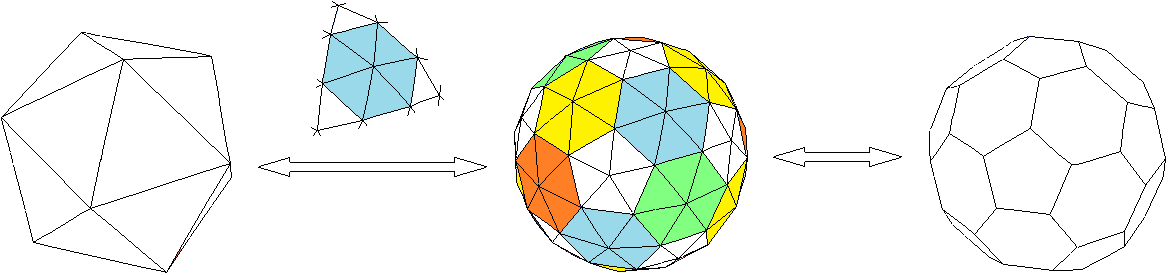
Aequivalenz_2

Man geht aus vom Ikosaeder und macht die 3²-Teilung (erstes Bild  →  zweites Bild), um das Kuppel-Deltaeder zu erhalten. Über dem Pfeil ist dargestellt, wie die Teilung einer Fläche des Ikosaeders mit anschließender Projektion der neu entstandenen Ecken auf die Umkugel sowie die Einfärbung im zweiten Bild zustande kommt. Von den jeweils 9 Dreiecken, die aus einer Ikosaeder-Fläche entstehen, werden die mittleren 6 Dreiecke gefärbt und die übrigen 3 Dreiecke bleiben weiß. Also treffen je 5 weiße Dreiecke zusammen, und zwar an den ursprünglichen 12 Ecken des Ikosaeders (E₅ = 12). Wegen F = 180 ergibt sich E₆ = 80 .

Die weißen Fünfecke und die farbigen Sechsecke ebnet man ein (zweites Bild  →  drittes Bild). Es bleiben 12 gleichseitige Fünfecke und 20 gleichseitige Sechsecke übrig, mit der Abfolge "5-6-6" an allen Ecken, also ein Ikosaederstumpf.

Alle Schritte sind umkehrbar; alle drei Körper haben die gleiche Umkugel.

Also ist ein 3²-Ikosaeder auch ein Tri-Ikosaederstumpf.

Vorsicht: Stellt man aus einem Ikosaeder einen Ikosaederstumpf her (durch Abschneiden der Ecken auf dem Drittel der Kanten), so ist dies nicht der rechte Körper, denn es wird zunächst die Umkugel kleiner. Will man also vom Ikosaeder über den Ikosaederstumpf zum Kuppel-Deltaeder kommen, schneidet man erst die Ecken des Ikosaeders ab, trianguliert alle Flächen (drittes Bild  →  zweites Bild) und projiziert die Mittelpunkte der Fünf- und der Sechsecke auf die Ikosaederstumpf-Umkugel. Schließlich vergrößert man den ganzen Körper, indem alle Ecken auf die Kugel mit gleichem Mittelpunkt und Radius 1 projiziert werden.

Nun kann man durch weitere Teilungen der Flächen der bis hierhin behandelten Polyeder beliebig viele Kuppel-Deltaeder herstellen. Die folgende Tabelle zeigt dies bis F ≤ 1000 .

		`F`	`E₅` `+` `E₆`
1.	Ikosaeder	`20`	`12` `+` `0`
2.	Tri-Hexa-Antiprisma	`24`	`12` `+` `2`
3.	Tri-Tetraederstumpf	`28`	`12` `+` `4`
4.	Tri-Dodekaeder	`60`	`12` `+` `20`
5.	`2²`-Ikosaeder = Tri-Ikosidodekaeder	`80`	`12` `+` `30`
6.	`2²`-Tri-Hexa-Antiprisma	`96`	`12` `+` `38`
7.	`2²`-Tri-Tetraederstumpf	`112`	`12` `+` `46`
8.	Tri-Abschräg-Dodekaeder	`140`	`12` `+` `60`
9.	`3²`-Ikosaeder = Tri-Ikosaederstumpf	`180`	`12` `+` `80`
10.	`3²`-Tri-Hexa-Antiprisma	`216`	`12` `+` `98`
11.	`2²`-Tri-Dodekaeder	`240`	`12` `+` `110`
12.	`3²`-Tri-Tetraederstumpf	`252`	`12` `+` `116`
13.	`4²`-Ikosaeder = `2²`-Tri-Ikosidodekaeder	`320`	`12` `+` `150`
14.	`4²`-Tri-Hexa-Antiprisma	`384`	`12` `+` `182`
15.	`4²`-Tri-Tetraederstumpf	`448`	`12` `+` `214`
16.	`5²`-Ikosaeder	`500`	`12` `+` `240`
17.	`3²`-Tri-Dodekaeder	`540`	`12` `+` `260`
18.	`2²`-Tri-Abschräg-Dodekaeder	`560`	`12` `+` `270`
19.	`5²`-Tri-Hexa-Antiprisma	`600`	`12` `+` `290`
20.	`5²`-Tri-Tetraederstumpf	`700`	`12` `+` `340`
21.	`6²`-Ikosaeder = `2²`-Tri-Ikosaederstumpf = `3²`-Tri-Ikosidodekaeder	`720`	`12` `+` `350`
22.	`6²`-Tri-Hexa-Antiprisma	`864`	`12` `+` `422`
23.	`4²`-Tri-Dodekaeder	`960`	`12` `+` `470`
24.	`7²`-Ikosaeder	`980`	`12` `+` `480`

Die hier beschriebenen Kuppel-Deltaeder lassen sich nun noch weiter zusammenfassen. Den Ausführungen zu Bild 5 und Bild 9 folgend, können wir uns auf die 5 Grundtypen Ikosaeder, Tri-Hexa-Antiprisma, Tri-Tetraederstumpf, Tri-Dodekaeder und Tri-Abschräg-Dodekaeder beschränken.

Welche Kuppel-Deltaeder werden dadurch erfasst?
Unter den Platonischen Körpern, Archimedischen Körpern und Antiprismen (die alle Umkugeln aufweisen) wählen wir diejenigen aus, die aus Dreiecken, Fünfecken und Sechsecken aufgebaut sind. Durch Triangulierung der Fünf- und Sechsecke und anschließender Projektion der neu entstandenen Ecken auf die Umkugel erhalten wir ausnahmslos Polyeder, bei denen an jeder Ecke 5 oder 6 Kanten zusammentreffen (Kuppel-Deltaeder). Bei diesen wurde dann eine weitere Teilung der Flächen nach einem einfachen Muster in j² kleinere Dreiecke vorgenommen.

Mit j = 1 für die Grundtypen und j ≥ 2 für die Teilungen der Dreiecke erhalten wir die folgende Übersicht über das Gesamtergebnis dieser Seite.

j²-Ikosaeder

j²-Tri-Hexa-Antiprisma

j²-Tri-Tetraederstumpf

j²-Tri-Dodekaeder

j²-Tri-Abschräg-Dodekaeder

Die Teilung der Flächen in kleinere Dreiecke lässt sich auch anders als hier beschrieben durchführen; so kommt man auf weitere Kuppel-Deltaeder. Hier sind zwei Links dazu:
Tadeusz E. Dorozinski: Geodätische Kuppeln
Christopher J. Kitrick: Geodesic Domes

Publiziert 2016-06-12 Stand 2014-11-14

voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem

Manfred Börgens | zur Leitseite