Sphärische Triangulation
Teil 1
Geodätische Linien auf der Kugeloberfläche, hier kurz als Geodäten bezeichnet, sind Abschnitte von Großkreisen (d.h. Umfangslinien) der Kugel. Zwei Punkte der Kugeloberfläche werden durch eine Geodäte auf kürzestem Weg verbunden (sogar eindeutig, wenn die Punkte keine Antipoden sind). Ein Kugeldreieck oder sphärisches Dreieck ist ein Teil der Kugeloberfläche, der von drei Geodäten begrenzt wird. Mit Kugeldreiecken befasst sich die sphärische Trigonometrie (Formelsammlung).
Wir wollen im Folgenden immer vom Kugelradius 1 ausgehen. Wie in der ebenen Geometrie dienen die Seitenlängen und die Winkel von Kugeldreiecken als die wesentlichen Bestimmungsgrößen. Bei den grundlegenden Berechnungsformeln für Seiten, Winkel und Flächen von Kugeldreiecken stößt man aber schnell auf (teilweise überraschende) Abweichungen von den entsprechenden Formeln für ebene Dreiecke. Beispielsweise haben Kugeldreiecke unterschiedliche Winkelsummen ( > 180°). Noch interessanter ist, dass sich die Dreiecksfläche nur aus den Winkeln berechnen lässt, also ohne Kenntnis der Seitenlängen.
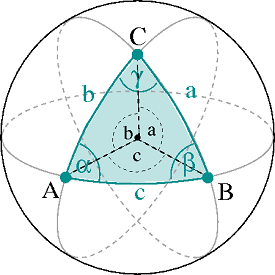
Bild 1
Man sieht in Bild 1, dass sich die Seitenlängen a, b, c auch als Winkel (am Kugelmittelpunkt) angeben lassen.
Eine Triangulation ist eine Zerlegung einer Fläche in Dreiecke. Ist diese Fläche die Oberfläche einer Kugel, so spricht man von einer sphärischen Triangulation.
Das kann man auch allgemeiner betrachten, indem man statt der Dreiecke beliebige Polygone zulässt. Einen Teil der Kugeloberfläche, der von Geodäten begrenzt wird, nennt man ein sphärisches Polygon. Eine Zerlegung der Kugeloberfläche in sphärische Polygone heißt sphärisches Polyeder. Offenbar gehört zu jedem normalen Polyeder, dessen sämtliche Ecken auf der Umkugel liegen, ein sphärisches Polyeder, denn statt der geraden Kanten kann man die zugehörigen Geodäten auf der Kugeloberfläche abtragen. Wir wollen im Folgenden nur auf diese Weise gebildete sphärische Polyeder betrachten (d.h. wir lassen z.B. keine Zweiecke zu, die es auf der Kugel gibt, aber bei gewöhnlichen Polyedern nicht). Links in Bild 2 ist ein Polyeder dargestellt, das sich auch leicht als sphärisches Polyeder vorstellen lässt, wenn man es zu einer vollen Kugel "aufbläst". Für solche sphärischen Polyeder gilt dann natürlich auch der Euler'sche Polyedersatz für die Anzahl der Flächen ( F ), der Ecken ( E ) und der Kanten ( K ) :
F + E = K + 2
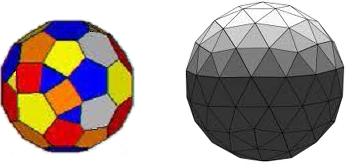
Bild 2
Rechts in Bild 2 sieht man ein Kugel-Deltaeder, also ein Polyeder nur aus Dreiecken, dessen Ecken alle auf der Umkugel liegen, und das zugehörige sphärische Deltaeder lässt sich wieder leicht vorstellen, indem man die Kanten durch geodätische Linien ersetzt. Um solche Gebilde geht es also hier bei diesem Problem. Die sphärische Triangulation führt auf sphärische Deltaeder; von diesen wollen wir einige besonders einfache näher untersuchen.
Bei der gewählten Terminologie muss angemerkt werden, dass Deltaeder üblicherweise Polyeder aus gleichseitigen Dreiecken bezeichnen. Diese Forderung soll hier entfallen, wenn "Kugel-" oder "sphärisches" vorangestellt wird.
Hier kommt die erste Aufgabe.
- Wird ein konvexes Polyeder nur von Dreiecken begrenzt, lässt sich der Euler'sche Polyedersatz vereinfachen. Leiten Sie dafür den Deltaedersatz her, indem Sie E und K unmittelbar aus F berechnen.
Der Deltaedersatz hat eine interessante Folgerung, denn er schränkt die Anzahl F der Dreiecke erheblich ein.
- Welche Werte kann F nach dem Deltaedersatz nicht annehmen?
- Zeigen Sie durch Beispiele, welche Werte F annehmen kann. Führen diese Beispiele auch zu sphärischen Triangulationen?
Viele Bilder von geodätischen Kuppeln (diese werden weiter unten noch genauer betrachtet) erwecken den Eindruck, dass es möglich ist, eine sphärische Triangulation aus zahlreichen identischen gleichseitigen Dreiecken zu bilden. Man schaue sich z.B. das folgende Foto einer Kuppel an (von dieser Kuppel ist nur noch eine Kugelkappe sichtbar, die weniger als eine Halbkugel umschließt); daneben ist eine halbkugelförmige Kuppel mit geringerer Maschendichte schematisch dargestellt.
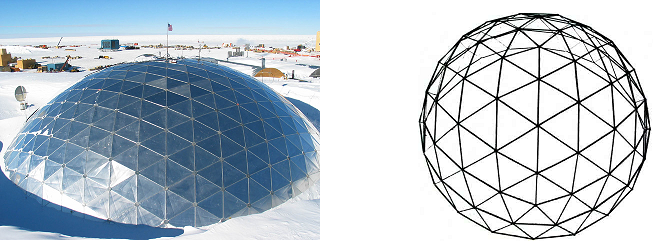
Bild 3
Links Amundsen Scott Dome der University of Antarctica
Erst bei genauerem Hinsehen erkennt man, dass in Bild 3 an den meisten Ecken sechs Dreiecke zusammenstoßen, aber an einigen nur fünf. Also können bei den zugehörigen Kugeldreiecken nicht alle Winkel identisch sein.
Wir befassen uns zunächst mit der regulären sphärischen Triangulation. Dabei sind alle Dreiecke gleichseitig und kongruent. Ihre Anzahl ist F ; an jeder Ecke sollen n Dreiecke zusammentreffen. F und n können zur Bestimmung der Flächeninhalte der Dreiecke herangezogen werden.
- Welche regulären sphärischen Triangulationen sind möglich?
- Verdeutlichen Sie sich den Fall F = 8 anhand des Erdglobus.
- Bestimmen Sie die Maße der Dreiecke, die bei der regulären sphärischen Triangulation vorkommen (Seitenlängen, Winkel, Flächeninhalte).
Eine feinere Triangulation erreicht man, indem die Kugeldreiecke aus der regulären sphärischen Triangulation in kleinere Dreiecke geteilt werden. Dadurch entstehen nicht-reguläre sphärische Triangulationen von hoher Symmetrie. Den einfachsten Fall, nämlich die Vervierfachung der Dreiecksanzahl, wollen wir hier berechnen. Man verbindet in jedem Dreieck die Seitenmittelpunkte durch Geodätische (Bild 4).
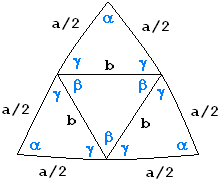
Bild 4
In Bild 4 hat das Ausgangsdreieck die Seitenlänge a und den Winkel α .
Für jedes Deltaeder aus den regulären sphärischen Triangulationen erhält man so ein neues sphärisches Deltaeder mit kleineren (aber nicht-kongruenten) sphärischen Dreiecken. Diese Triangulationen wollen wir wegen der Vervierfachung Tetra-Triangulationen nennen.
- Wieviele Dreiecke, Ecken und Kanten entstehen bei den Tetra-Triangulationen?
Leiten Sie das zunächst direkt aus der regulären Triangulation ab und überprüfen Sie Ihr Ergebnis mit dem Deltaedersatz.
- Bestimmen Sie die Maße dieser Dreiecke (Seitenlängen, Winkel, Flächeninhalte).
- Beschreiben und zählen Sie die Ecken anhand der Anzahl der anstoßenden Kanten und deren Winkel.
- Wie oft kommen welche Kantenlängen vor?
Anfangs wurde schon erklärt, dass Polyeder, deren Ecken auf einer Kugeloberfläche liegen, auf ein sphärisches Polyeder führen. Für die hier betrachteten sphärischen Deltaeder gilt offenbar auch die Umkehrung. Indem man benachbarte Ecken durch gerade Strecken verbindet, erhält man ein normales Kugel-Deltaeder. Damit ist die erste der beiden folgenden Fragen ganz einfach.
- Welche Polyeder entsprechen den regulären sphärischen Triangulationen?
- Welche Kantenlängen haben diese Polyeder?
Die bereits erwähnten geodätischen Kuppeln sind zu sphärischen Polyedern gehörige normale Polyeder, in der Regel mit sehr vielen Flächen. (Für ein Polyeder ist die Bezeichnung geodätisch erklärungsbedürftig: Sie bezieht sich darauf, dass alle Ecken auf einer Kugeloberfläche liegen). In der Architektur ersetzt man die (geodätischen) Kanten der sphärischen Polygone (meist Dreiecke) durch Stangen. Je mehr Dreiecke zur Bildung des Polyeders verwendet werden, desto ähnlicher wird die geodätische Kuppel einer Kugel. Natürlich wird meist nicht die volle "Kugel" errichtet, sondern nur eine "Halbkugel", so dass auch der Name "Kuppel" verständlicher wird. Die Dreiecke werden in der Regel verglast. Solche Bauwerke bestechen durch ihre Ästhetik und eine sehr große Stabilität bei geringem Eigengewicht (siehe Bild 3 links).
- Welche Längen müssen die Stangen der geodätischen Kuppeln haben, wenn die Kuppeln aus Tetra-Triangulationen enstehen?
Richard Buckminster Fuller hat die geodätischen Kuppeln in die Architektur eingeführt. Hier ist eine Briefmarke mit seinem Porträt:

Bild 5
Links zu geodätischen Kuppeln:
Website von Werner Brefeld - unverzichtbar für Mathematik-Ästheten
Leitseite direkt zu den Kuppeln
Wikipedia deutsch
Wikipedia englisch
Lösung
Kategorie: Geomathematik
Publiziert 2012-12-01 Stand 2011-10-03
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite




