Teil 2
In Teil 1 (Problem 81) wurden die drei Deltaeder unter den Platonischen Körpern betrachtet. Sie lieferten die Grundlage für die einzigen regulären sphärischen Triangulationen. Drei weitere sphärische Triangulationen ergaben sich aus der Aufteilung aller sphärischen Dreiecke in vier kleinere Dreiecke. Auf diese Weise wurde das sphärische Tetra-Tetraeder, das sphärische Tetra-Oktaeder und das sphärische Tetra-Ikosaeder gebildet. Nur das letzte - mit 80 Seiten - hat Ähnlichkeit mit den in der Architektur vorkommenden geodätischen Kuppeln. Das sind (möglichst regelmäßige) Polyeder, deren Ecken alle auf der Umkugel liegen. Ihnen entsprechen sphärische Polyeder - man muss dazu lediglich die geraden Kanten durch die zugehörigen Geodätischen auf der Umkugel ersetzen. In diesem Sinne sind das Tetra-Ikosaeder und das sphärische Tetra-Ikosaeder aus Problem 81 äquivalent.
Nun soll ein weiteres sphärisches Deltaeder gebildet werden. Der zugrundeliegende Platonische Körper ist hier das Dodekaeder (Bild 1).
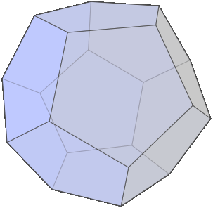
Bild 1
Wie kommt man vom Dodekaeder zu einer sphärischen Triangulation? Naheliegend ist, in einem ersten Schritt jedes der zwölf Fünfecke in fünf gleichschenklige Dreiecke aufzuteilen, deren Basis eine Dodekaederkante ist und die als dritte Ecke den Mittelpunkt des Fünfecks haben. Diese Mittelpunkte werden dann auf die Umkugel projiziert. Wir erhalten so ein Kugel-Deltaeder (siehe Teil 1), das wir Penta-Dodekaeder nennen wollen (Bild 2).
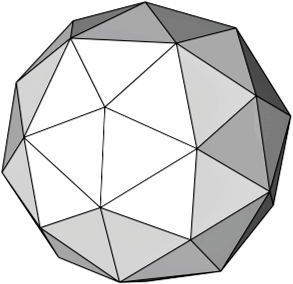
Bild 2
Das zugehörige sphärische Polyeder erhält man wieder durch Ersetzung der Kanten durch Geodätische. Dieses sphärische Penta-Dodekaeder hätte man auch erhalten, wenn man das sphärische Dodekaeder als Ausgangskörper gewählt hätte und dort die Mittelpunkte der sphärischen Fünfecke mit den Dodekaederecken durch Geodätische verbunden hätte (dann entfällt die Projektion).
Penta-Dodekaeder und sphärisches Penta-Dodekaeder zeichnen sich durch Eigenschaften aus, die man beispielsweise beim Tetra-Ikosaeder nicht findet: