Sphärische Triangulation
Teil 2
Die Lösung steht im unteren Teil der Seite.
In Teil 1 (Problem 81) wurden die drei Deltaeder unter den Platonischen Körpern betrachtet. Sie lieferten die Grundlage für die einzigen regulären sphärischen Triangulationen. Drei weitere sphärische Triangulationen ergaben sich aus der Aufteilung aller sphärischen Dreiecke in vier kleinere Dreiecke. Auf diese Weise wurde das sphärische Tetra-Tetraeder, das sphärische Tetra-Oktaeder und das sphärische Tetra-Ikosaeder gebildet. Nur das letzte - mit 80 Seiten - hat Ähnlichkeit mit den in der Architektur vorkommenden geodätischen Kuppeln. Das sind (möglichst regelmäßige) Polyeder, deren Ecken alle auf der Umkugel liegen. Ihnen entsprechen sphärische Polyeder - man muss dazu lediglich die geraden Kanten durch die zugehörigen Geodätischen auf der Umkugel ersetzen. In diesem Sinne sind das Tetra-Ikosaeder und das sphärische Tetra-Ikosaeder aus Problem 81 äquivalent.
Nun soll ein weiteres sphärisches Deltaeder gebildet werden. Der zugrundeliegende Platonische Körper ist hier das Dodekaeder (Bild 1).
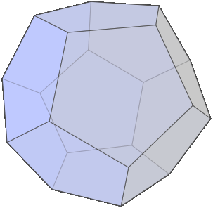
Bild 1
Wie kommt man vom Dodekaeder zu einer sphärischen Triangulation? Naheliegend ist, in einem ersten Schritt jedes der zwölf Fünfecke in fünf gleichschenklige Dreiecke aufzuteilen, deren Basis eine Dodekaederkante ist und die als dritte Ecke den Mittelpunkt des Fünfecks haben. Diese Mittelpunkte werden dann auf die Umkugel projiziert. Wir erhalten so ein Kugel-Deltaeder (siehe Teil 1), das wir Penta-Dodekaeder nennen wollen (Bild 2).
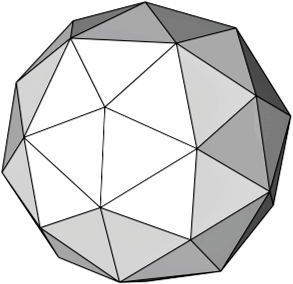
Bild 2
Das zugehörige sphärische Polyeder erhält man wieder durch Ersetzung der Kanten durch Geodätische. Dieses sphärische Penta-Dodekaeder hätte man auch erhalten, wenn man das sphärische Dodekaeder als Ausgangskörper gewählt hätte und dort die Mittelpunkte der sphärischen Fünfecke mit den Dodekaederecken durch Geodätische verbunden hätte (dann entfällt die Projektion).
Penta-Dodekaeder und sphärisches Penta-Dodekaeder zeichnen sich durch Eigenschaften aus, die man beispielsweise beim Tetra-Ikosaeder nicht findet:
- Alle 60 Dreiecke sind kongruent.
- An jeder Ecke sind alle Winkel gleich. (Das bedeutet natürlich nicht, dass am ganzen Polyeder alle Winkel gleich sind.)
- Die ursprünglichen Dodekaederkanten bleiben erhalten (als Basis der gleichschenkligen Dreiecke).
Es gibt aber eine Gemeinsamkeit zwischen Tetra-Ikosaeder und Penta-Dodekaeder. Beide sind Kugel-Deltaeder, an deren Ecken 5 oder 6 Kanten zusammentreffen. Diese Eigenschaft findet man bei den meisten geodätischen Kuppeln in der Architektur (dort werden allerdings meist nicht die vollständigen Polyeder errichtet, sondern nur Strukturen, die einer Halbkugel oder einer Kugelkappe ähnlich sind; siehe die Bilder in Problem 81).
Das führt auf die erste Aufgabe:
- Ein Kugel-Deltaeder weise an allen Ecken 5 oder 6 zusammentreffende Kanten auf. Berechnen Sie die Anzahl der "5er-Ecken" und "6er-Ecken" in Abhängigkeit von der Anzahl E der Ecken bzw. von der Anzahl F der Dreiecke.
Nun soll die sphärische Triangulation und die zugehörige geodätische Kuppel wie in Problem 81 analysiert werden. Wir gehen wieder vom Kugelradius 1 aus.
- Wenden Sie den Deltaedersatz aus Problem 81 auf das Penta-Dodekaeder an, indem Sie E und K unmittelbar aus F berechnen.
- Bestimmen Sie die Maße der Kugeldreiecke im sphärischen Penta-Dodekaeder (Seitenlängen, Winkel, Flächeninhalte).
- Beschreiben und zählen Sie die Ecken anhand der Anzahl der anstoßenden Kanten und deren Winkel.
- Welche Längen müssen die Stangen des Penta-Dodekaeders, also der zugehörigen geodätischen Kuppel haben?
Lösung
- Ein Kugel-Deltaeder weise an allen Ecken 5 oder 6 zusammentreffende Kanten auf. Berechnen Sie die Anzahl der "5er-Ecken" und "6er-Ecken" in Abhängigkeit von der Anzahl E der Ecken bzw. von der Anzahl F der Dreiecke.
Die gesuchten Anzahlen wollen wir mit E5 und E6 bezeichnen. Nach dem Deltaedersatz aus Problem 81 gilt:
K = (3/2)·F E = E5 + E6 = F/2 + 2
Von jeder 5er-Ecke gehen 5 Kanten aus. Jeder Kante gehört aber gleichzeitig zu einer anderen Ecke. Das gilt entsprechend für die 6er-Ecken. Damit muss gelten:
(5/2)·E5 + (6/2)·E6 = K = (3/2)·F
⇒ 5·E5 + 6·(E - E5) = 3·F
⇒ 5·E5 + 6·(F/2 + 2 - E5) = 3·F
Die Antwort auf die erste Frage lautet also:
E5 = 12
E6 = E - 12 = F/2 - 10
Das ist ein interessantes Ergebnis!
- In allen geodätischen Kuppeln, an deren Ecken 5 oder 6 Dreiecke zusammentreffen - auch in den sehr großen mit Tausenden Dreiecken - , gibt es konstant viele, nämlich (nur) genau 12 5er-Ecken.
- Es gibt keine Kugel-Deltaeder, die nur 6er-Ecken haben.
- Drei dieser Kugel-Deltaeder haben wir schon kennen gelernt: In Problem 81 das Ikosaeder ( E6 = 0 ) und das Tetra-Ikosaeder ( E6 = 30 ), und hier das Penta-Dodekaeder ( E6 = 20 ).
- Wenden Sie den Deltaedersatz aus Problem 81 auf das Penta-Dodekaeder an, indem Sie E und K unmittelbar aus F berechnen.
Aus F = 60 folgt: E = 32 K = 90
- Bestimmen Sie die Maße der Kugeldreiecke im sphärischen Penta-Dodekaeder (Seitenlängen, Winkel, Flächeninhalte).
Wir beginnen mit den Winkeln: In den "5er-Ecken" bzw. in den "6er-Ecken" sind alle Winkel gleich groß, also gleich 2π/5 = 72° bzw. 2π/6 = 60° . Jedes Dreieck hat somit zwei Winkel von 60° und einen von 72° (Bild 3).
Für die Seitenlängen verwenden wir die Formel (2) aus Problem 81. Dort liegt die Seite a dem Winkel α gegenüber. In der zweiten Zeile ist cos a freigestellt worden:
cos α = - cos β·cos γ + sin β·sin γ·cos a
cos a = (cos α + cos β·cos γ) / (sin β·sin γ)
Ist a die Basis des gleichschenkligen Dreiecks, so ist α = 72° und β = γ = 60° . Damit erhalten wir a ≈ 0,7297 ≈ 41,81° .
Ist a eine der beiden anderen Seiten, so ist α = β = 60° und γ = 72° . Damit erhalten wir a ≈ 0,6524 ≈ 37,38° (Bild 3).
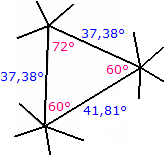
Bild 3
Die Dreiecksfläche A beträgt 1/60 der Kugeloberfläche, also 4π/60 = π/15 . A ergibt sich auch als Winkelsumme abzüglich π , also 2π/5 + 2π/6 + 2π/6 - π = π/15 .
- Beschreiben und zählen Sie die Ecken anhand der Anzahl der anstoßenden Kanten und deren Winkel.
Dazu müssen nur noch die Ergebnisse der ersten und dritten Frage zusammengefasst werden:
Das (sphärische) Penta-Dodekaeder hat 12 Ecken, an denen 5 Kanten im Winkel von 72° zusammentreffen, und 20 Ecken, an denen 6 Kanten im Winkel von 60° zusammentreffen.
- Welche Längen müssen die Stangen des Penta-Dodekaeders, also der zugehörigen geodätischen Kuppel haben?
Wie in Problem 81 berechnet man für ein Bogenstück a einer Geodätischen auf der Einheitskugel die zugehörige Sehne zu 2·sin a/2 .
Für a wurden bereits die Werte a ≈ 0,7297 bzw. a ≈ 0,6524 angegeben.
Die Stangenlängen der geodätischen Kuppel betragen also ca. 0,7136 und 0,6409 .
Die kürzeren Stangen sind im Verhältnis zu den längeren um etwa 10 % kürzer, was ausreichend gering ist, um der Kuppel ein harmonisches Gesamtbild zu geben (Bild 2).
Publiziert 2013-04-08 Stand 2011-10-03
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite


