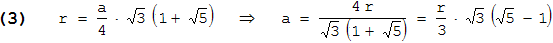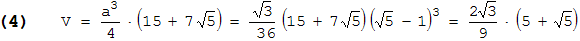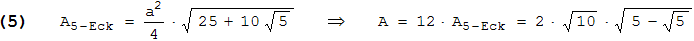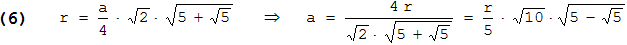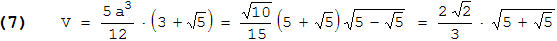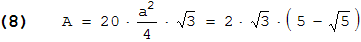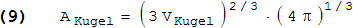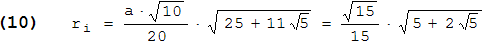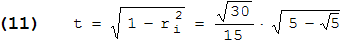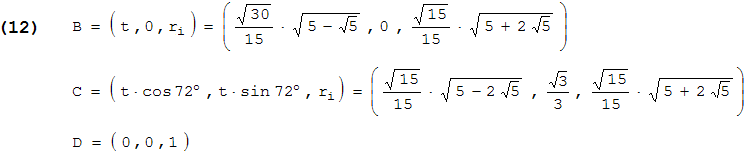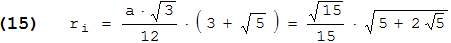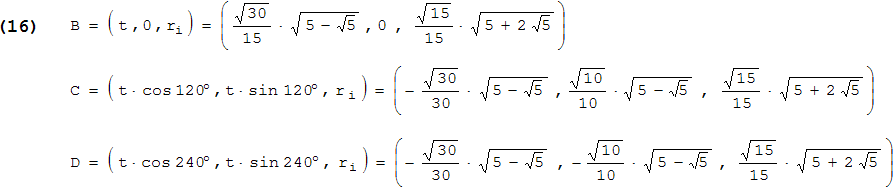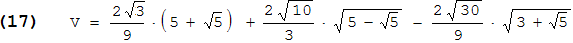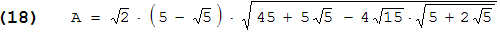Sphärische Triangulation
Teil 3 Teil 4
Die Lösung steht im unteren Teil der Seite.
In den beiden ersten Teilen der "Sphärischen Triangulation" wurden sowohl sphärische Deltaeder als auch die zugehörigen normalen Kugel-Deltaeder, wie sie beim Bau Geodätischer Kuppeln vorkommen, untersucht. Sowohl das Penta-Dodekaeder als auch das Tetra-Ikosaeder weisen in recht guter Näherung Kugelgestalt auf.
Es soll darauf hingewiesen werden, dass hier - wie auch in den Problemen 81 und 82 - spezielle Deltaeder untersucht werden, deren Kanten nicht gleich lang sein müssen und deren Ecken sämtlich auf der Umkugel liegen. Der Grund dafür liegt in der ursprünglichen Problemstellung der sphärischen Triangulation, als deren Weiterführung die Betrachtung der Geodätischen Kuppeln naheliegend erscheint.
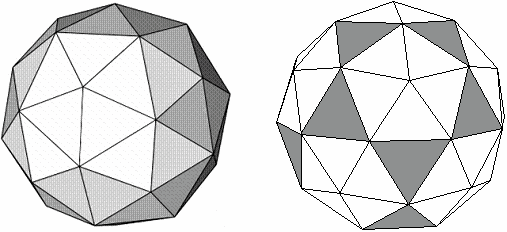
Bild 1 Penta-Dodekaeder und Tetra-Ikosaeder
In der Literatur findet man das Penta-Dodekaeder unter dem Namen Pentakisdodekaeder, siehe [1]; dieses sollte nicht verwechselt werden mit dem Pentagondodekaeder, welches lediglich eine andere Bezeichnung für das Dodekaeder ist. Üblicherweise wird von Deltaedern gefordert, dass sie nur aus gleichseitigen Dreiecken bestehen (dann gibt es nur endlich viele, siehe [2]); dies gilt in den hier vorgelegten drei Problemen zur sphärischen Triangulation nicht.
Unter den Platonischen Körpern füllt das Dodekaeder die Umkugel am besten aus, also insbesondere zu einem höheren Anteil als das Ikosaeder, obwohl dieses mehr Flächen aufweist. Also liegt es nahe, dass wir für Penta-Dodekaeder und Tetra-Ikosaeder ebenfalls das Volumen berechnen und vergleichen.
Die Ausfüllung der Umkugel durch ein Kugel-Deltaeder ist eine naheliegende Frage für die Erbauer Geodätischer Kuppeln. Aber für eine möglichst gute "Kugelgestalt" lassen sich auch andere Kriterien heranziehen. Wir wollen hier drei Kriterien betrachten:
- In welchem Verhältnis v1 steht das Volumen des Kugel-Deltaeders zum Volumen der Umkugel? D.h. zu welchem Anteil füllt das Kugel-Deltaeder seine Umkugel aus?
- In welchem Verhältnis v2 steht die Oberfläche des Kugel-Deltaeders zur Oberfläche der Umkugel?
- In welchem Verhältnis v3 steht die Oberfläche einer Kugel mit gleichem Volumen zur Oberfläche des Kugel-Deltaeders? (Diese Maßzahl heißt Sphärizität eines Polyeders.)
v1 , v2 , v3 wollen wir zuerst für die beiden Platonischen Körper berechnen. In den meisten Formelsammlungen werden die Maße der Platonischen Körper in Abhängigkeit von der Kantenlänge angegeben. Hier - wie auch in den Problemen 81 und 82 - wird für den Radius der Umkugel r = 1 vorgegeben. Die erste Aufgabe wird es also sein, mit Hilfe der Formelsammlungen (von denen zahlreiche im Internet verfügbar sind) die folgenden Werte anzugeben.
(*) Dabei sollen möglichst einfache Formeln gefunden werden, die keine Wurzeln im Nenner aufweisen.
Für Dodekaeder und Ikosaeder mit r = 1 sind zu berechnen:
- Kantenlänge
- Volumen
- Oberfläche
- die drei Maßzahlen für die Kugelgestalt v1 , v2 , v3
Die Ergebnisse erlauben einen Vergleich dieser beiden Platonischen Körper bzgl. ihrer Kugelgestalt. Lässt sich das auf die Geodätischen Kuppeln Penta-Dodekaeder und Tetra-Ikosaeder übertragen? Die Konstrukteure Geodätischer Kuppeln werden sich dabei vor allem dafür interessieren, wieviel Platz unter ihrer Kuppel ist (v1), und wie "kugelförmig" sie wirkt (v2 und v3).
Wir beginnen mit einer Methode, die ein Koordinatensystem einbezieht und die Volumen und Oberfläche beider Körper berechnen hilft. Der Mittelpunkt der Umkugel der Kugel-Deltaeder soll in den kartesischen (x,y,z)-Koordinaten im Ursprung liegen. Eine beliebige Fläche eines Kugel-Deltaeders ist dann ein Dreieck mit den Ecken B, C, D mit B =(b1,b2,b3) usw. Dessen Flächeninhalt findet man in Formelsammlungen zur analytischen Geometrie:
(1) Flächeninhalt des Dreiecks BCD: AΔ = ||(B-D)×(C-D)||/2
Über die Summierung dieser Dreiecksflächen erhält man die Oberflächen von Penta-Dodekaeder und Tetra-Ikosaeder.
Das Volumen der beiden Kugel-Deltaeder ist die Summe der Volumina der (unregelmäßigen) Tetraeder mit diesen Dreiecken als Grundflächen und der Spitze im Ursprung. Die Formel dafür findet man leicht:
(2) Volumen des Tetraeders OBCD: VΔ = |(B×C)·D|/6
In (1) und (2) bezeichnet ||·|| die Norm, |·| den Betrag, × das Kreuzprodukt und · das Skalarprodukt von Vektoren.
Also bleibt noch die Berechnung der Koordinaten von B, C, D . Beim Penta-Dodekaeder sind alle Dreiecke kongruent, also ist nur ein AΔ bzw. VΔ zu berechnen. Beim Tetra-Ikosaeder gibt es zwei verschiedene Dreiecke.
Wir legen das Dodekaeder so in das Koordinatensystem, dass eine Fläche (Fünfeck) parallel zur (x,y)-Ebene liegt, also alle Ecken des Fünfecks bei z = ri (Inkugelradius) liegen. ri kann der Formelsammlung für die Platonischen Körper entnommen werden, sollte aber wie in (*) dargestellt werden. Dann sind B und C zwei Ecken des Fünfecks und D = (0,0,1). Die x- und y-Koordinaten von B und C sind leicht anzugeben, wenn man beachtet, dass B und C auf einem Kreis liegen und ihr Winkelabstand auf diesem Kreis 72° beträgt. Die Darstellung der Koordinaten wird besonders einfach, wenn man z.B. B so legt, dass y = 0 ist.
- Berechnen Sie Volumen, Oberfläche sowie die Maßzahlen v1 , v2 , v3 für das Penta-Dodekaeder mit r = 1 .
Das Ikosaeder legen wir ebenfalls so, dass eine Fläche (Dreieck BCD ) bei z = ri (Inkugelradius) liegt. Die x- und y-Koordinaten von B, C und D berechnet man analog zum Dodekaeder. Dieses Dreieck wird nun in vier kleinere Dreiecke geteilt; zur Erinnerung wird hier nochmal ein Ausschnitt des sphärischen Tetra-Ikosaeders aus Problem 81 (um die Eckpunkte ergänzt) gezeigt:
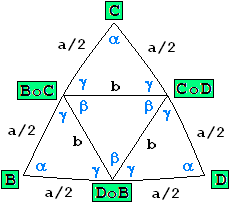
Bild 2
Bei den Punkten BoC usw. ist zu beachten, dass die Seitenmitten im Dreieck BCD auf die Kugeloberfläche projiziert werden müssen. Dann kann man wie beim Penta-Dodekaeder mit (1) die Flächeninhalte des mittleren Dreiecks und eines der Randdreiecke (z.B. mit den Ecken B, BoC, DoB ) berechnen, sowie die zugehörigen Volumina der Tetraeder mit (2).
- Berechnen Sie Volumen, Oberfläche sowie die Maßzahlen v1 , v2 , v3 für das Tetra-Ikosaeder mit r = 1 .
- Vergleichen Sie das Penta-Dodekaeder und das Tetra-Ikosaeder anhand der Maßzahlen v1 , v2 , v3 .
1. Bemerkung: Beim Penta-Dodekaeder kann man auch ohne die Koordinaten-Rechnung auskommen, indem man rein geometrisch argumentiert. Denn das Penta-Dodekaeder entsteht, indem jedem Fünfeck des Dodekaeders eine regelmäßige Pyramide aufgesetzt wird, und deren Maße sind leicht zu berechnen. Alle Ergebnisse sollen wieder (*) genügen. Dies kann als Zusatzaufgabe durchgeführt werden.
2. Bemerkung: In den Problemen 81 und 82 wurden auch die Längen der "Stangen" in den Geodätischen Kuppeln berechnet, also u.a. die Kantenlängen von Penta-Dodekaeder und Tetra-Ikosaeder. Dies ist ein weiterer Weg, um direkt zu einem numerischen Wert für die Oberfläche der Kugel-Deltaeder zu gelangen. Man kann dies als Probe für die bereits erhaltenen Ergebnisse rechnen.
Quellen
[1] Werner Brefeld: Geodätische Kuppeln
[2] Jürgen Köller: Deltaeder
Lösung
Wir beginnen mit der Kantenlänge des Dodekaeders. In Problem 82 wurde der Wert 0,7136 angegeben, aber das ist nur ein Näherungswert. Schauen wir in eine Formelsammlung. Dort wird meist der Radius der Umkugel in Abhängigkeit von der Kantenlänge angegeben, und nicht umgekehrt:
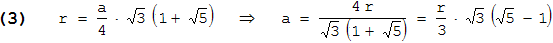
Die letzte Umformung haben wir vorgenommen, weil a eine "schöne" Form haben soll, und zwar wie in (*).
Dabei wurde die erste Form von a mit √3·(√5 - 1) erweitert. - Für das Volumen findet man mit (3) und r = 1 :
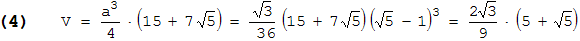
Den letzten Ausdruck erhält man durch einfaches Ausmultiplizieren. - Für die Oberfläche A schauen wir zuerst die Formel für den Flächeninhalt A5-Eck des regelmäßigen Fünfecks nach und setzen dann a aus (3) (mit r = 1 ) ein:
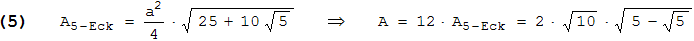
Für die letzte Gleichung multipliziert man a2 und dann a4 aus und schreibt dann (a4)1/2 mit der hinteren Wurzel (aus A5-Eck ) unter eine gemeinsame Wurzel.
Nun geht es weiter mit dem Ikosaeder. Wir beginnen wieder mit der Kantenlänge:
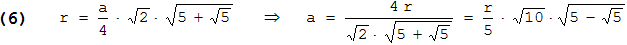
Dabei wurde die erste Form von a zuerst mit (5 - √5)1/2 erweitert, und dann mit √10 . - Für das Volumen findet man mit (6) und r = 1 :
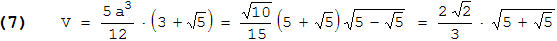
Bei der letzten Umrechnung spaltet man a3 in a·a2 auf und multipliziert zuerst alle Terme außer der Doppelwurzel aus. Dieses Produkt enthält einen Faktor 5 + √5 , den man als ((5 + √5)1/2)2 schreibt. Der Rest geht mit der 3. binomischen Formel. - Die Oberfläche ist das 20-fache der Dreiecksfläche mit a als Seitenlänge:
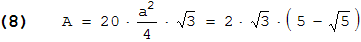
Nun können wir die drei Maßzahlen v1 , v2 , v3 berechnen. Für eine möglichst gute "Kugelgestalt" sollten alle drei möglichst nahe bei 1 liegen.
Für v1 wird das Volumen des Kugel-Deltaeders aus (4) bzw. (7) durch (4/3)·π geteilt. Für v2 wird die Oberfläche aus (5) bzw. (8) durch 4·π geteilt.
Für die Sphärizität v3 erhält man zunächst aus VKugel = (4/3)·π·r3 und AKugel = 4·π·r2 :
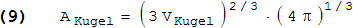
Dann teilt man den Wert in (9) durch die Oberfläche aus (5) bzw. (8); für VKugel setzt man das Volumen aus (4) bzw. (7) ein.
| |
Dodekaeder |
Ikosaeder |
| v1 |
0.6649 |
0.6055 |
| v2 |
0.8367 |
0.7619 |
| v3 |
0.9105 |
0.9393 |
Bei v1 und v2 schneidet also das Dodekaeder besser ab, bei der Sphärizität das Ikosaeder.
Es geht weiter mit dem Penta-Dodekaeder. Wie in der Aufgabenstellung beschrieben, legen wir zunächst das Dodekaeder so in ein (x,y,z)-Koordinatensystem, dass sein Mittelpunkt in (0,0,0) und eine Seitenfläche (Fünfeck) parallel zur (x,y)-Ebene mit z > 0 liegt. Dann ist z der Inkugelradius ri , den wir für r = 1 mit (3) so umformen können, dass er a nicht mehr enthält und (*) erfüllt:
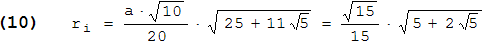
Diese Berechnung ist leicht nachzuvollziehen, wenn man a als (a2)1/2 schreibt und dann a2 unter die hintere Wurzel zieht. - Zwei Ecken des Penta-Dodekaeders ( B und C ) sind dann identisch mit zwei benachbarten Ecken des Fünfecks; die dritte ( D ) liegt im "höchsten" Punkt der Umkugel, also in (0,0,1) . Der Einfachheit halber legen wir B in (t,0,ri) ; dabei ist t der Radius des Kreises, auf dem die Ecken des Fünfecks liegen. Schaut man sich den Schnitt durch die Umkugel an, der durch B und D geht, so bilden die Radien der Umkugel, der Inkugel und des Kreises ( r = 1, ri und t ) ein rechtwinkliges Dreieck. Somit gilt:
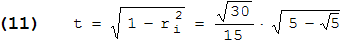
Da C auf dem Fünfeck zu B benachbart liegt, und auch auf dem Kreis mit Radius t , müssen die x- und y-Koordinaten eine Drehung um 72° machen. Das führt auf x = t·cos 72° und y = t·sin 72° . Nun ist cos 72° = (√5 - 1)/4 und sin 72° = √2·(5 + √5)1/2/4 . So erhalten wir alle Koordinaten für ein Dreieck des Penta-Dodekaeders:
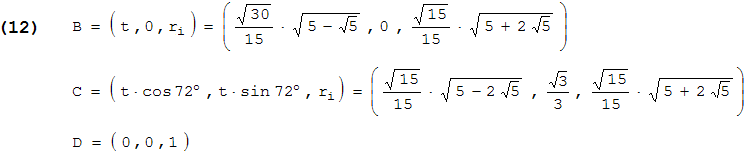
Mit (2) berechnen wir VΔ und damit das Volumen des Penta-Dodekaeders:
(13) V = 60·VΔ ≈ 3.5049
(Das wird man natürlich nicht von Hand rechnen, auch nicht mit dem Taschenrechner. Für die Kreuz- und Skalarprodukte schreibt man ein kleines Programm, z.B. in Excel, noch einfacher in Mathematica.)
Mit (1) berechnen wir AΔ und damit die Oberfläche des Penta-Dodekaeders:
(14) A = 60·AΔ ≈ 11.3967
Als letztes führen wir die Berechnungen zum Tetra-Ikosaeder durch. Das Ikodaeder legen wir wieder so in ein (x,y,z)-Koordinatensystem, dass sein Mittelpunkt in (0,0,0) und eine Seitenfläche (Dreieck) parallel zur (x,y)-Ebene mit z = ri liegt. Wir beginnen wieder mit dem Inkugelradius für r = 1 und rechnen analog (10).
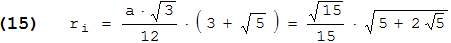
Die Ecken von BCD in Bild 2 liegen auf einem Kreis, in einem Winkelabstand von 120° . Wir können also ganz analog zum Penta-Dodekaeder vorgehen und B in (t,0,ri) legen. Da der Inkugelradius der gleiche ist wie beim Dodekaeder, hat t den gleichen Wert wie in (11). So erhalten wir alle Koordinaten für ein Dreieck des Ikosaeders:
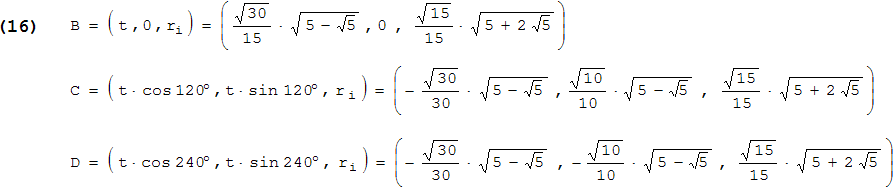
Dann ist BoC = ((B+C)/2) / ||(B+C)/2|| , also der Mittelpunkt zwischen B und C , dividiert durch dessen Abstand von (0,0,0) ; analog für CoD und DoB . Für das mittlere Dreieck in Bild 2 setzen wir in (1) und (2) die Koordinaten von BoC, CoD und DoB ein (von diesen Dreiecken gibt es 20 auf dem Tetra-Ikosaeder). Für eines der anderen, nicht-gleichseitigen Dreiecke setzen wir in (1) und (2) die Koordinaten von B, BoC und DoB ein (von diesen Dreiecken gibt es 60 auf dem Tetra-Ikosaeder). Mit den Bezeichnungen VΔm und AΔm für das Mitteldreieck sowie VΔa und AΔa für das andere Dreieck erhalten wir mit (2) bzw. (1):
(17) V = 20·VΔm + 60·VΔa ≈ 3.6587
(18) A = 20·AΔm + 60·AΔa ≈ 11.6659
Nun können wir die drei Maßzahlen v1 , v2 , v3 berechnen. Das geht analog zu Dodekaeder und Ikosaeder (oben hinter (8) bis zur Tabelle).
| |
Penta-Dodekaeder |
Tetra-Ikosaeder |
| v1 |
0.8367 |
0.8735 |
| v2 |
0.9069 |
0.9283 |
| v3 |
0.9791 |
0.9843 |
Dass diese beiden Kugel-Deltaeder besser abschneiden als die beiden Platonischen Körper, überrascht natürlich nicht. Letztere wird man wohl auch nicht als Geodätische Kuppeln errichten. - Bei allen drei Werten schneidet also das Tetra-Ikosaeder besser ab als das Penta-Dodekaeder. Insbesondere bedeutet das ein größeres Volumen der Geodätischen Kuppel und eine bessere Sphärizität; bei v2 ist allerdings zu bemerken, dass das Tetra-Ikosaeder auch einen höheren Materialverbrauch erfordert.
Zur 1. Bemerkung: Das Volumen einer aufgesetzten Pyramide ist gleich Grundfläche × Höhe/3 . Die Grundfläche ist die Fünfeckfläche aus (5); die Höhe ist 1 - ri , siehe (10). Durch einfaches Ausmultiplizieren erhält man so das Volumen der 12 aufgesetzten Pyramiden; dazu wird noch das Dodekaedervolumen aus (4) addiert. Damit kann für das Volumen des Penta-Dodekaeders sogar ein exakter Wert angegeben werden:
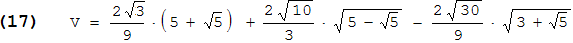
Auch die Oberfläche lässt sich auf geometrischem Wege exakt darstellen. Ein Dreieck des Penta-Dodekaeders hat als Basis die Kantenlänge a des Dodekaeders aus (3) mit r = 1 . Benennt man die beiden anderen Seiten mit ag , so ist ag2 = (1 - ri)2 + t2 = 2·(1 - ri) wegen (11). Als Flächeninhalt des Dreiecks ergibt sich daraus (√15 - √3)·(ag2 - a2/4)1/2/6 . 60 dieser Dreiecke fügen sich zur Oberfläche zusammen:
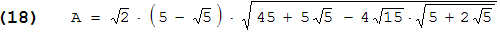
Rechnet man (17) und (18) numerisch aus, erhält man näherungsweise natürlich wieder die Werte aus (13) und (14).
Publiziert 2013-06-09 Stand 2012-04-11
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens |
zur Leitseite