Briefmarke des Monats Oktober 2004

Israel 1997   Michel 1446   Scott 1324

Julia-Menge für die Iterationsfunktion  f(z) = z² + 0.286 + 0.0115 i

Diese Briefmarke zeigt einen Ausschnitt einer Julia-Menge. Auf dem Anhang der Marke sieht man einen größeren Ausschnitt, aber noch interessanter ist die Formel am Rand des Anhangs:  z -> z² + c     c = 0.2860 + 0.0115 i . Jede Julia-Menge ist durch eine komplexe Funktion eindeutig bestimmt; durch die Angabe dieser Funktion sind wir somit in der Lage, die Entstehung der Abbildung auf der Marke nachzuvollziehen.

Julia-Mengen sind nach dem französischen Mathematiker Gaston Maurice Julia benannt, der sie zu Beginn des 20. Jahrhunderts erforschte. Diese Mengen haben außerordentliche mathematische und ästhetische Eigenschaften. Viele dieser Mengen sind fraktal, also "selbst-ähnlich" (d.h. sie weisen in allen Skalierungen die gleiche Struktur auf, siehe auch die Monatsbriefmarke Januar 2004).

Durch die Festlegung einer Funktion  f : C -> C  auf der Menge der komplexen Zahlen wird die zugehörige Julia-Menge definiert als die Menge aller komplexen Zahlen  z_o , für die die iterierten Funktionswerte  f^k(z_o)  für alle natürlichen  k  eine beschränkte Menge bilden. Hier bedeutet  f^k  nicht die  k-te Potenz, sondern die  k-fache Anwendung der Funktion  f . Dies soll anhand der Funktion auf der Briefmarke  f(z) = z² + c  mit  c = 0.286 + 0.0115 i  erklärt werden. Die Graphiken in Bild 1 zeigen beispielhaft, was die iterierte Anwendung von  f  für verschiedene Startwerte  z_o  bewirkt. Der Startwert ist jeweils farbig gezeichnet, die iterierten Werte  f^k(z_o)  sind jeweils durch einen Polygonzug verbunden. Man kann zeigen, dass die  f^k(z_o)  betragsmäßig beliebig groß werden, wenn für irgend ein  k  |f^k(z_o)| > 2  wird. Deshalb ist aus Bild 1 zu entnehmen, dass  z_o = 0.025 + 0.1 i  und  z_o = 0.7 + 0.195 i  nicht zur Julia-Menge gehören.


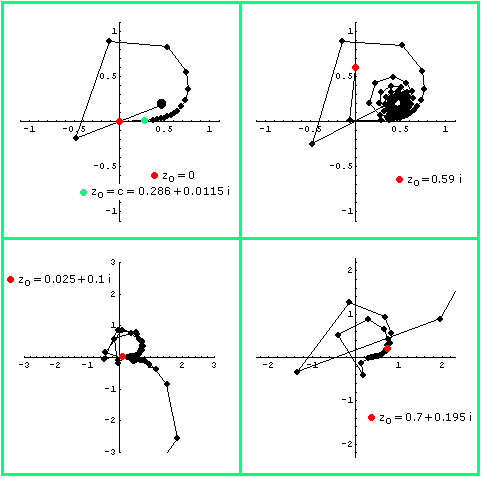
Bild 1     Iterationen  f^k(z_o)  für  f(z) = z² + 0.286 + 0.0115 i 

Nur die schwarzen Flächen im Bild auf der Briefmarke stellen Punkte der Julia-Menge dar. Bild 2 stellt diese Menge ohne die umgebenden farbigen Gebiete und - soweit es die graphische Auflösung zulässt - vollständig dar. (Ein solches Bild kann nie ganz genau sein, da man für das Zeichenprogramm eine (endliche) Iterationstiefe vorgeben muss. Die runden und eiförmigen schwarzen Gebiete fasern noch mehr aus, wenn man die Iterationstiefe hochsetzt.) Zur Orientierung in der komplexen Zahlenebene sind am Rand vier Zahlen eingetragen.


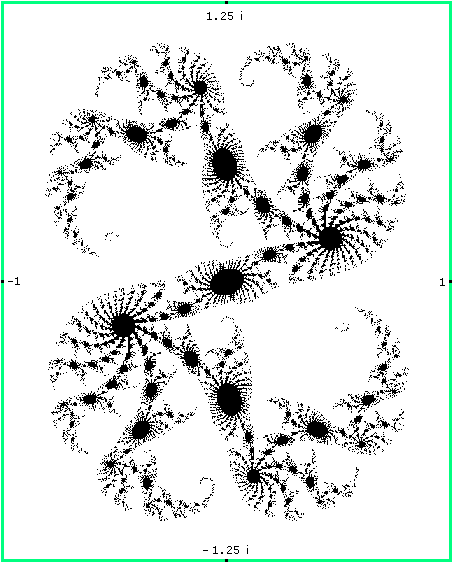
Bild 2     Julia-Menge für  f(z) = z² + 0.286 + 0.0115 i 

Die Lage (innerhalb der Julia-Menge) der fünf Anfangswerte aus Bild 1 sieht man in Bild 3:


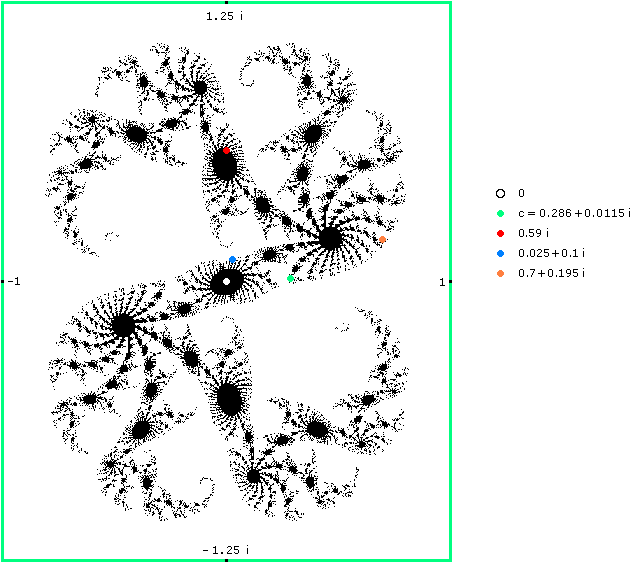
Bild 3     Julia-Menge für  f(z) = z² + 0.286 + 0.0115 i 

Die Marke zeigt nur einen kleinen, aber stark vergrößerten Ausschnitt der Julia-Menge. Was bedeuten die farbigen Flächen um die Julia-Menge herum, die dem Bild einen erheblichen zusätzlichen Reiz verschaffen? Da jeder dieser farbigen Punkte  z  nicht zur Julia-Menge rechnet, ist die Folge  f^k(z)  unbeschränkt. Die Farbe eines Punktes gibt nun an, wie "schnell" sich die  f^k(z_o)  von  z_o  entfernen. Es gibt zahlreiche Programme, viele davon im Internet, mit denen man Julia-Mengen zusammen mit ihren farbigen Umgebungen zeichnen kann. Die Farbgestaltung ist allerdings willkürlich. Bild 3 zeigt die vollständige Julia-Menge für  f(z) = z² + 0.286 + 0.0115 i  mit anderen Farben als auf der Briefmarke.


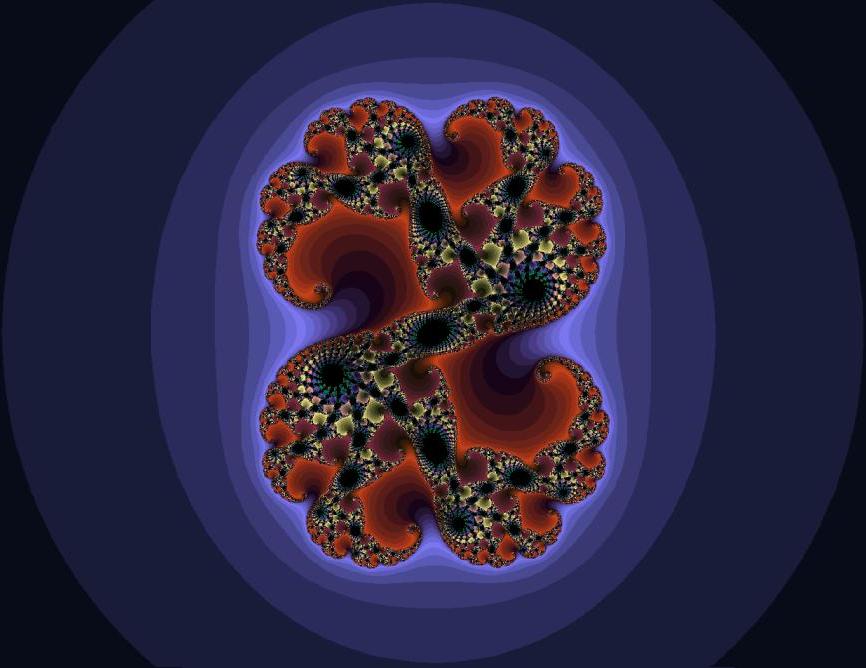
Bild 4     Julia-Menge für  f(z) = z² + 0.286 + 0.0115 i 


Wann ist eine Julia-Menge zusammenhängend? Dazu gibt es einen wichtigen Satz der fraktalen Geometrie:

Ist die Iterationsfunktion von der Form  f(z) = z² + c , so ist die zugehörige Julia-Menge genau dann zusammenhängend, wenn der Nullpunkt zur Menge gehört, d.h. wenn  f^k(0)  eine beschränkte Folge ist.

Da  f(0) = c , lässt sich der Satz auch so formulieren:

Ist die Iterationsfunktion von der Form  f(z) = z² + c , so ist die zugehörige Julia-Menge genau dann zusammenhängend, wenn  c  zur Menge gehört, d.h. wenn  f^k(c)  eine beschränkte Folge ist.

Im folgenden wollen wir uns nur noch mit Julia-Mengen für  f(z) = z² + c  befassen. (Alle diese Mengen sind punktsymmetrisch zum Nullpunkt.) Der Satz liefert dann ein einfaches Kriterium zur Überprüfung des Zusammenhangs der Menge.  f^k(0)  ist in der linken Graphik von Bild 1 abgebildet. Die Julia-Menge auf der Briefmarke ist also zusammenhängend, obwohl das auf Bild 2 nicht erkennbar ist. Die scheinbar abgetrennten Teilmengen hängen in Wirklichkeit durch dünne "Fäden" zusammen.

Der oben angegebene Satz teilt also alle Julia-Mengen in zwei Klassen. In Bild 5 wird je ein Vertreter dieser Klassen dargestellt.


Bild 5     Zusammenhängende und unzusammenhängende Julia-Menge

Es stellt sich die Frage, ob man diejenigen komplexen Zahlen  c , für die die Julia-Menge zusammenhängend ist, übersichtlich darstellen kann. Das geht in der Tat: Diese Zahlen bilden nämlich die berühmte Mandelbrot-Menge, abgebildet in Bild 6. Die Mandelbrot-Menge, benannt nach Benoit Mandelbrot, ist demnach eine Art Landkarte für Julia-Mengen, denn an ihr kann man ablesen, welche Julia-Mengen zusammenhängend sind. Liegt  c  im Inneren des großen herzförmigen Bereichs der Mandelbrot-Menge, so erhält man ziemlich kompakt aussehende Julia-Mengen (z.B. linke Graphik in Bild 5), die man sich mit wachsendem Abstand des  c  von  0  als Verzerrungen des Einheitskreises vorstellen kann. Je weiter man sich dem Rand der Mandelbrot-Menge nähert, desto zerfaserter sind die zugehörigen Julia-Mengen.  c = 0.286 + 0.0115 i  ist in Bild 6 als roter Punkt eingezeichnet. Dieses  c  liegt also stark am Rand der Mandelbrot-Menge, deshalb weist die zugehörige Julia-Menge eine komplizierte fraktale Struktur auf. - Zur Orientierung in Bild 6: Der äußerste linke Punkt der Mandelbrot-Menge, also die "Antennenspitze", ist der Punkt  c = -2 . Die Spitze der Einbuchtung rechts, ganz nah beim roten Punkt, ist der Punkt  c = 0.25 .


Bild 6     Mandelbrot-Menge

Julia-Mengen weisen eine fantastische Vielfalt auf. Ein Zoom in die Detailstruktur ist von hohem ästhetischen Reiz. Es ist sehr empfehlenswert, dies selbst mit fertigen oder selbstgeschriebenen Programmen auszuprobieren (Beispiel).


Weitere fraktale Mengen auf Briefmarken:   Koch'sche Schneeflocke     Cantor-Menge