Briefmarke des Monats Januar 2004

  Schweden 2000

  Michel 2207 / 2208

Fraktale "Schneeflocke" von Niels Fabian Helge von Koch (1870 - 1924)

Im Jahre 1904, also vor 100 Jahren, konstruierte der Stockholmer Mathematikprofessor Helge von Koch eine Kurve, die überall stetig, aber nirgends differenzierbar ist. Diese Kurve, die "Koch'sche Schneeflocke", erlangte später große Bekanntheit als besonders schönes Beispiel einer fraktalen Kurve. Die schwedische Doppelbriefmarke zeigt insgesamt vier dieser Schneeflocken, aber leider alle nur unvollständig; die jeweils linken Schneeflocken auf jeder Marke zeigen die 3. Iteration und die jeweils rechten die 4. Iteration - dies wird im nächsten Absatz erklärt. Am unteren Markenrand steht links der Name des Graphikers (A. KORNESTEDT 2000), rechts steht: HELGE VON KOCHS SNÖFLINGEKURVA (Schneeflockenkurve).

Konstruktion der Koch'schen Schneeflocke

Mit der Koch'schen Schneeflocke ist nicht die Fläche, sondern ihr Rand gemeint. Dieser ist die Grenzkurve einer Iteration von Polygonen (Vielecken). Sie beginnt mit einem gleichseitigen Dreieck (0. Iterationsstufe). Jeder weitere Schritt ersetzt alle Polygonseiten aus der vorigen Stufe durch vier Seiten, deren Länge  1/3  der Ausgangsseite beträgt, nach dem folgenden Muster:

Bei dieser Ersetzung muss die "Zacke" so liegen, dass sie die Polygonfläche vergrößert. Hier sieht man die iterative Entwicklung der Koch'schen Schneeflocke:

Die ersten vier Bilder - also die 0. bis 3. Iteration - kann man noch gut nachvollziehen, bei den beiden letzten Bildern wird die graphische Auflösung zu ungenau. (Auf der Briefmarke ist allerdings wegen der starken Vergrößerung auch die 4. Iteration noch gut zu erkennen.) Alle diese Kurven sind nur Näherungen der Koch'schen Schneeflocke, die sich selbst nicht zeichnen lässt. Aber die geringen Unterschiede zwischen den letzten drei Bildern zeigen, dass das rechte Bild einen guten Eindruck von der Grenzkurve gibt; weitere Iterationen wären bei dieser Bildgröße für unser Auge nicht mehr unterscheidbar.

Die Koch'sche Schneeflocke ist eine fraktale Kurve

Ein geometrisches Objekt wird als Fraktal bezeichnet, wenn es die Eigenschaft der "Selbst-Ähnlichkeit" aufweist. Anhand der Schneeflocke lässt sich das gut erklären: Der Rand zeigt in allen Skalierungen dieselbe Struktur, d.h. bei beliebiger Vergrößerung sieht der Rand immer gleich aus. Solche selbst-ähnlichen Gebilde findet man auch in der Natur, etwa bei Küsten, Wolkenrändern oder Bergsilhouetten. Die Koch'sche Schneeflocke unterscheidet sich von diesen natürlichen Fraktalen dadurch, dass ihre Erzeugung durch einen vorgegebenen Algorithmus determiniert ist.

Länge und Flächeninhalt der Koch'schen Schneeflocke

Das Ausgangsdreieck soll die Seitenlänge  1  haben. Dann ist die  n-te Iteration ein Polygon mit

3·4ⁿ  Seiten
Seitenlänge  (1/3)ⁿ
Umfang  3·(4/3)ⁿ
Flächeninhalt  √3·(8 - 3·(4/9)ⁿ)/20

Von diesen Formeln muss wohl nur der Flächeninhalt erklärt werden. Hat ein gleichseitiges Dreieck die Seitenlänge  a , so ist seine Fläche  (a²·√3)/4 . Das Ausgangsdreieck (0. Iteration) hat also den Flächeninhalt  √3/4 . Bei der i-ten Iteration kommen  3·4^i-1  Dreiecke hinzu, jedes mit Seitenlänge  (1/3)ⁱ . In der  i-ten Iteration vergrößert sich also der Flächeninhalt um  (3·4^i-1·(1/9)ⁱ·√3)/4 = (√3/12)·(4/9)^i-1 . Addiert man zur Summe dieser Terme für  i = 1 , ... , n  (endliche geometrische Reihe) noch  √3/4 , so erhält man  √3/4 + (√3/12)·(1 - (4/9)ⁿ)·(9/5) = √3·(8 - 3·(4/9)ⁿ)/20 .

Der Umfang und der Flächeninhalt nehmen also mit wachsendem  n  zu, aber nicht in gleichem Maße: Lässt man  n  gegen Unendlich streben, erhält man, dass die Koch'sche Schneeflocke eine unendlich lange Kurve ist, die einen endlichen Flächeninhalt umschließt, nämlich  (2/5)·√3 .

Fraktale Dimension

Die Koch'sche Schneeflocke ist eigentlich keine Kurve. Damit ist nicht die Tatsache gemeint, dass man sie nicht richtig als durchgehende Linie zeichnen kann. Aber sie ist in gewisser Weise kein eindimensionales Gebilde wie z.B. eine Gerade oder eine Parabel. Man kann der Schneeflocke eine Dimension zuweisen, die zwischen 1 und 2 liegt, somit ist sie irgendwo zwischen Kurven und Flächen einzuordnen. Dies gilt, obwohl alle Iterationen Polygone sind, also eindimensionale Gebilde.

Fraktalen Gebilden kann man eine fraktale Dimension  D  zuordnen. Die Koch'sche Schneeflocke hat die Dimension

D = log 4 / log 3 = 1.26...

Wie kommt diese Dimension zustande? Die Koch'sche Schneeflocke gehört zu einer Klasse von geometrischen Gebilden, die iterativ durch eine einfache Ersetzungsregel definiert sind. Vor jedem Iterationsschritt hat man ein geometrisches Objekt, bestehend aus einer endlichen Anzahl immer gleichartiger "Grundgebilde" (bei der Schneeflocke sind dies Strecken, die ein gleichseitiges Polygon bilden). In jedem Iterationsschritt werden alle diese Grundelemente ersetzt durch mehrere Grundelemente in kleinerem Maßstab. Diese Ersetzungsregel soll hier für die Schneeflocke noch einmal wiederholt werden:

Für die Bestimmung der fraktalen Dimension spielen nun bei der Ersetzungsregel zwei Zahlen eine Rolle, nämlich  c  für den Faktor der Vervielfachung der Grundelemente in einem Iterationsschritt und  r  für den Verkleinerungsfaktor dieser Grundelemente. Bei der Schneeflocke wird in jedem Schritt eine Strecke ersetzt durch vier Strecken der 1/3-fachen Länge, also ist hier  c = 4  und  r = 3 . Die allgemeine Formel für die fraktale Dimension solcher "determinierten" geometrischen Gebilde ist

D = log c / log r

Die Dimension der Koch'schen Schneeflocke ist größer als 1, weil die Schneeflocke gewissermaßen ein sehr "rauer" Rand einer Fläche ist. Bei der Iteration von Kurven kann man  D  mit einiger Berechtigung auch als "Rauheitsgrad der Grenzkurve" auffassen.

Für das Konzept der fraktalen Dimension soll noch ein weiteres Beispiel gezeigt werden, das Sierpinski-Dreieck. Im Gegensatz zur Koch'schen Schneeflocke sind die Grundelemente des Sierpinski-Dreiecks keine eindimensionalen Gebilde, sondern ebene Flächen, also zweidimensional. In jedem Iterationsschritt liegt eine Fläche mit positivem Flächeninhalt vor. Man geht aus von einer gleichseitigen Dreiecksfläche. Hier ist die Ersetzungsregel:

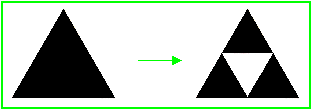
Mit dieser Ersetzungsregel entsteht ein schönes Fraktal, das auf den polnischen Mathematiker Waclaw Sierpinski (1882 - 1969) zurückgeht:

Für das Sierpinski-Dreieck gilt  c = 3  und  r = 2 . Dabei ist zu beachten, dass für die Berechnung der fraktalen Dimension der "Maßstab" für den Verkleinerungsfaktor immer für die Längeneinheiten genommen wird. In einem Iterationsschritt des Sierpinski-Dreiecks haben die kleineren Dreiecke die halbe Seitenlänge vom Ausgangs-Dreieck, also ist  r = 2 . So ergibt sich  D = log 3 / log 2 = 1.58... Somit ist das Sierpinski-Dreieck der Koch'schen Schneeflocke ziemlich ähnlich, denn beides sind geometrische Gebilde mit einer fraktalen Dimension zwischen 1 und 2, liegen also zwischen Kurven und Flächen (aber das Sierpinski-Dreieck ist "rauer" als die Koch'sche Schneeflocke). Die Iterationen laufen allerdings von zwei entgegengesetzten Ausgangspositionen: Bei der Koch'schen Schneeflocke wird eine Kurve immer weiter verlängert (mit unendlichem Grenzwert), während beim Sierpinski-Dreieck eine Fläche fortgesetzt ausgedünnt wird (mit Grenzwert 0 für den Flächeninhalt).

Die fraktale Dimension stimmt für "normale" Kurven, Flächen oder Körper, die iterativ mit Ersetzungsregeln erzeugt werden können, mit der üblichen ganzzahligen Dimension überein. Für einfache Beispiele sieht man das sofort: So kann man etwa eine Strecke im n-ten Iterationsschritt in  rⁿ  gleich große Teilstrecken zerlegen und erhält so  c = r , also  D = 1 . Ein Quadrat lässt sich im n-ten Iterationsschritt in  r²ⁿ  gleich große Teilquadrate zerlegen, dann ist  c = r² , also  D = 2 . Ein Würfel lässt sich im n-ten Iterationsschritt in  r³ⁿ  gleich große Teilwürfel zerlegen, also ist  c = r³  und  D = 3 .

Natürliche Fraktale

Eine andere Definition der fraktalen Dimension, die aber zum gleichen Ergebnis führt, ist aus dem Studium von natürlichen fraktalen Kurven entstanden.

Als Beispiel soll die Bestimmung der Länge  L  einer Küstenlinie dienen. Man kann versuchen, eine grobe Näherung für  L  zu erhalten, indem man auf einer Karte die Küstenlinie mit einem relativ großen Längenstab "abgreift", z.B. wie im folgenden Bild:

Sei nun  s  die Länge des Stabes und  L(s)  die Länge des Polygonzuges. Ist etwa im Bild  s = 1  gewählt, so ist  L(1) = 11 .  L(s)  als Näherung für  L  aufzufassen, zudem mit der Vorstellung, dass  lim L(s) = L  für  s -> 0 , führt aber in die Irre. Denn tatsächlich strebt  L(s)  für  s -> 0  gegen Unendlich.

Eine (endliche) Küstenlänge gibt es also eigentlich nicht. Welche Länge einer Küste zugeschrieben wird, hängt von der Feinheit des Messinstrumentes ab. Nun stößt man aber bei tatsächlichen Vermessungen immer wieder auf eine Regelmäßigkeit, nämlich  L(s) = k·s^1-D  mit Konstanten  k > 0  und  D > 1 , die von der Küstengestalt abhängen. Dieses  D  entpuppt sich als die oben beschriebene fraktale Dimension, wenn man das Verfahren mit den Längenstäben auf "determinierte" Fraktale anwendet. Im nächsten Bild wird die Koch'sche Schneeflocke mit Längenstäben (in Grün) der Maße  s = 1, 1/3, 1/9  abgegriffen:

Hier wurde  s = (1/3)ⁿ  gewählt. Weiter oben sind die zugehörigen Längen der Polygonzüge schon angegeben worden:  L(s) = 3·(4/3)ⁿ . Wegen  n = - log s / log 3  und der Logarithmusregel  a^log b = b^log a  ist  L(s) = 3·s^{log 3/4 / log 3} = 3·s^{(log 3 - log 4) / log 3} = 3·s^{1 - log 4 / log 3} .

Daher ist hier  k = 3  und (wie erwartet)  D = log 4 / log 3 . Also ist (gerundet)  L(s) = 3·s^-0.26.

Zurück zur Küstenlinie:
Für etliche Küsten auf der Erde wurden die fraktalen Dimensionen ermittelt. Es ist nicht verwunderlich, dass es Küsten unterschiedlicher "Rauheit" gibt. Hier sind drei Beispiele:

Australien   D = 1.13
Großbritannien   D = 1.25
Norwegen   D = 1.52

Küsten sind also keine eindimensionalen Kurven, sondern fraktale Gebilde wie die Koch'sche Schneeflocke.

Ein räumliches Fraktal

Ein räumliches Analogon zum Sierpinski-Dreieck ist das Sierpinski-Tetraeder. Man startet mit einem gleichseitigen Tetraeder. Bei jedem Iterationsschritt wird ein Tetraeder durch vier Tetraeder mit halber Seitenlänge ersetzt, indem man vom Ausgangs-Tetraeder alle sechs Kanten halbiert und dann jede der vier Ecken mit den drei nächstgelegenen Halbierungspunkten zu einem Tetraeder verbindet. Es gibt eine ungarische Briefmarke aus dem Jahr 1996, die die 2. Iteration zeigt:

Das folgende Bild zeigt die ersten vier Iterationen:

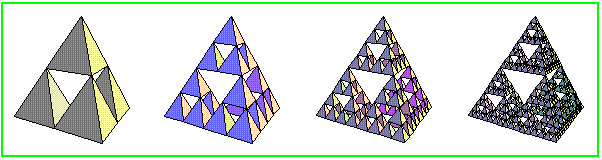
Welche Dimension hat das Sierpinski-Tetraeder? Wegen  c = 4  und  r = 2  ist  D = log 4 / log 2 = 2 . Das ist ein bemerkenswertes Ergebnis. Das Sierpinski-Tetraeder hat eine ganzzahlige fraktale Dimension! Durch fortgesetzte Ausdünnung von 3D-Objekten erhält man ein geometrisches Objekt, das genau die (fraktale) Dimension einer Fläche hat.

Waclaw Sierpinski ist auch mit einer Briefmarke geehrt worden (Polen 1982):

Literatur zu Fraktalen

MATHEMATICA-Programm zum Zeichnen der Koch'schen Schneeflocke

Hier geht's zum fraktalen Pythagoras-Baum.


Weitere fraktale Mengen auf Briefmarken:   Julia-Menge     Cantor-Menge