Georg Cantor ist am besten bekannt als Begründer der Mengenlehre. Dies steht auch am Rand des Sonderstempels, der oben links abgebildet ist. Die Stadt Halle in Sachsen-Anhalt, in der Cantor als Professor wirkte, ehrte ihn mit diesem Stempel zu seinem 150. Geburtstag. Die dort abgebildete Formel
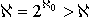0
ist ein Satz Cantors über transfinite Kardinalzahlen.
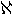steht für die Mächtigkeit der Menge der reellen Zahlen R, 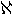0 für die Mächtigkeit der Menge der natürlichen Zahlen N und 
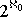für die Mächtigkeit der Potenzmenge (Menge aller Teilmengen) einer Menge der Mächtigkeit 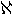0. Der Cantor'sche Satz sagt also zweierlei aus: R hat eine größere Mächtigkeit als N, und die Mächtigkeit von R ist gleich der Mächtigkeit der Potenzmenge von N.
Die Cantor-Menge
Die Cantor-Menge ist eine fraktale Teilmenge des reellen Intervalls [0,1]. Sie wird iterativ nach einem Verfahren gewonnen, das auf der oberen Briefmarke gezeigt wird: Im Schritt n wird aus allen Teilintervallen der Menge Mn-1 jeweils das mittlere Drittel entfernt, um die Menge Mn zu erzeugen; der Start erfolgt mit M0 = [0,1]. Alle verbleibenden Teilintervalle sollen ihre Endpunkte enthalten. Für M2 bedeutet das:
M2 = [0, 1/9] ∪ [2/9, 1/3] ∪ [2/3, 7/9] ∪ [8/9, 1]
Die Cantor-Menge M ist dann die Menge aller Zahlen in [0,1], die in jeder Menge Mn liegen, d.h.
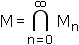
M0 bis M3 sind auf der Briefmarke abgebildet.
In M liegen sicherlich alle Endpunkte aller Intervalle. Aber M enthält noch viel mehr Zahlen. Wir wollen zur Beschreibung von M die Elemente von [0,1] in der Basis 3 ausdrücken (triadische Darstellung). (Dann ist also z.B. 0,13 gleich 1/3 im Dezimalsystem, und 0,023 gleich 2/9). Durch vollständige Induktion lässt sich dann ohne große Mühe nachweisen:
(1)
Mn besteht aus 2n disjunkten, abgeschlossenen Teilintervallen der Länge 1/3n; Mn hat also die Gesamtlänge (2/3)n.
(2)
Die Randpunkte der Teilintervalle in Mn (n > 0) sind die 2n+1 Zahlen 0, 1 und 0,x..xy3 mit 0 bis n-1 Ziffern x = 0 oder x = 2 und y = 1 oder y = 2. (Für n = 3 sind das die 16 Zahlen 03 0,0013 0,0023 0,013 0,023 0,0213 0,0223 0,13 0,23 0,2013 0,2023 0,213 0,223 0,2213 0,2223 13, vgl. die unterste Menge auf der Marke.)
Bei der Induktion von Mn nach Mn+1 werden alle diese Zahlen übernommen; hinzu kommen weitere 2n+1 Zahlen, indem zu allen linken Intervallrändern in Mn (das sind 0 und die Zahlen mit y = 2) 1/3n+1 = 0,0..013 und 2/3n+1 = 0,0..023 addiert werden (für die neu entstehenden Teilintervalle in Mn+1).
(3)
Wir betrachten nun nicht nur die Randpunkte der Teilintervalle, sondern beliebige Punkte x ∈ M. Sie liegen jeweils in einer Folge von Intervallen In ⊂ Mn mit der Länge 1/3n. Deren linke Randpunkte wachsen monoton, die rechten Randpunkte fallen monoton. Also ist der Durchschnitt dieser Intervalle ein einzelner Punkt (nämlich x). x hat nach (2) für jedes n in den ersten n Nachkommastellen der triadischen Darstellung nur 0en und 2en. Somit enthält die triadische Darstellung von x insgesamt nur 0en und 2en. Umgekehrt gilt aber auch, dass jede solche Zahl in M liegt, denn (0,x1 x2 x3 ...)3 liegt in In mit dem linken Randpunkt (0,x1...xn)3 .
So ist z.B. 0,022022022...3 = (4/13)10 ∈ M.
Man beachte, dass auch die rechten Randpunkte der Teilintervalle, die nach (2) eine abbrechende triadische Darstellung mit 1 am Ende aufweisen, sich nur mit 0en und 2en schreiben lassen: 0,x..x13 = 0,x..x0222...3 . - Die Folge von 0en und 2en lässt sich verstehen als Abfolge der Richtungen L/R (für links und rechts), da ein Punkt x ∈ M bei jedem Iterationsschritt entweder im linken oder im rechten Teilintervall liegt.
Die Cantor-Menge hat interessante Eigenschaften:
Überabzählbarkeit
Obwohl die Iteration nur einen (schwer vorstellbaren) dünnen "Staub" hinterlässt, hat die Cantor-Menge die Mächtigkeit
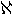, hat also gleich viele Elemente wie die Menge der reellen Zahlen. Für den Beweis nutzt man aus, dass auch das Intervall [0,1] die Mächtigkeit 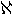hat. Es wird eine Bijektion f: M → [0,1] konstruiert: f((0,x1x2x3...)3) = (0,y1y2y3...)2) mit yk = xk/2 . Das Bild dieser Abbildung sind alle Zahlen in [0,1] in Binärdarstellung.
Fraktal
Die Cantor-Menge ist selbstähnlich, sieht also bei allen Ausschnittvergrößerungen gleich aus. Diese Eigenschaft fraktaler Mengen wurde bereits anhand der Koch'schen Schneeflocke erklärt. Analog zur Schneeflocke berechnen wir die fraktale Dimension von M:
D = log 2 / log 3 ≈ 0.63093
Dabei steht die 2 für die Vervielfachung der Grundstruktur - bei jedem Iterationsschritt werden aus jedem Einzelintervall zwei neue Intervalle - und die 3 für den Verkleinerungsfaktor dieser Intervalle.
Fraktaler Baum
Auf der unteren Briefmarke ist ein fraktaler Baum zu sehen. Hier ist die Konstruktionsvorschrift für die einzelnen Iterationsschritte und die Selbstähnlichkeit von anderer Natur als bei der Cantor-Menge und der Koch'schen Schneeflocke. Beim fraktalen Baum wird nicht in jedem Schritt jedes strukturbildende Teil durch andere (ähnliche, aber kleinere) Teile ersetzt, sondern es werden neue Strukturteile hinzufügt. Bei dem Baum auf der Briefmarke sind dies die V-förmigen Astverzweigungen an den Spitzen. Die bereits vorhandenen Äste werden nicht ersetzt, sondern es werden weitere angefügt. Die so entstehende fraktale Menge B besteht dann aus den Grenzwerten der Astspitzen. Hier liegt eine starke Analogie zur Cantor-Menge: Die Punkte in B lassen sich wieder eindeutig charakterisieren als Folge von Richtungen L oder R, sind also auch überabzählbar.
Der Graphiker hat den Faktor 2 für die Verkleinerung der V-förmigen Verzweigungen gewählt. Da sich in jedem Schritt die Anzahl der Verzweigungen verdoppelt, erhalten wir als fraktale Dimension: D = log 2 / log 2 = 1
Ein weiteres Fraktal wird auf der Briefmarke # 37 dargestellt.
Im Hintergrund beider Marken sieht man die Andeutung von Julia-Mengen. Eine solche Menge ist auch auf der Briefmarke # 45 zu sehen.
Die Cantor-Menge und fraktale Bäume wurden bereits 1982 von Benoît B. Mandelbrot in seinem fundamentalen Buch The Fractal Geometry of Nature behandelt.