Briefmarke des Monats September 2004

Schweiz 1994   Michel 1517   Scott 939

Jakob Bernoulli (1654 - 1705)

Jakob Bernoulli war der älteste der zahlreichen Mathematiker in seiner Familie. Er erhielt 1687 den Lehrstuhl für Mathematik an der Universität Basel, der dann über 100 Jahre lang ununterbrochen von Bernoullis besetzt blieb. Jakobs direkter Nachfolger auf diesem Lehrstuhl war sein jüngerer Bruder Johann I Bernoulli, der ihn wiederum an seinen Sohn Johann II Bernoulli "vererbte". Das Verhältnis der beiden Brüder, die beide als sehr bedeutende Mathematiker gelten, wandelte sich mit fortschreitendem Alter von Kooperation über Rivalität zu offener Feindschaft.

Jakob Bernoulli lebte in einer Zeit, in der die Mathematik die größten Fortschritte seit der Antike machte. In die zweite Hälfte des 17. Jahrhunderts fiel die Entwicklung der Infinitesimalrechnung durch Newton und Leibniz, zu der auch Jakob Bernoulli bedeutende Beiträge lieferte, u.a. zu unendlichen Reihen, zu Differentialgleichungen (die Bernoulli'sche Differentialgleichung  y' = p(x)·y + q(x)·yⁿ  ist nach Jakob benannt) und zur Variationsrechnung.

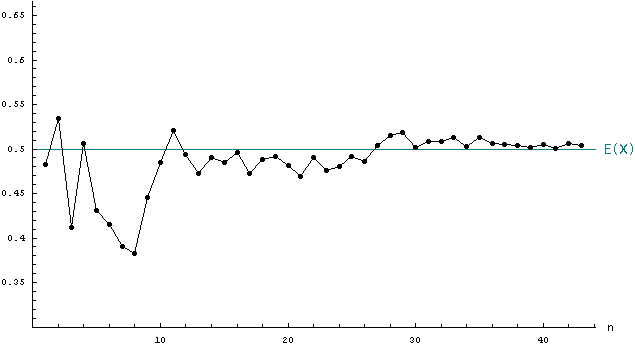
Jakob Bernoulli wurde durch sein Buch Ars Conjectandi ("Kunst des Vermutens") ein Pionier der Wahrscheinlichkeitstheorie. Er untersuchte darin u.a. den Zusammenhang zwischen der relativen Häufigkeit von Ereignissen und ihrer Wahrscheinlichkeit. Das "Schwache Gesetz der großen Zahlen" von Bernoulli stellt diesen Zusammenhang exakt dar. Aus Ars Conjectandi stammen der Begriff "Stochastik" und die Bernoulli'schen Zahlen. Auf der Briefmarke ist eine allgemeinere Variante des Schwachen Gesetzes der großen Zahlen dargestellt. Man sieht dort einen Graphen und die Formel



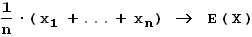
X  steht für eine reelle Zufallsvariable mit Erwartungswert  E(X)  und  n  "Realisationen"  x₁, ..., x_n. Die Formel sagt aus, dass der Erwartungswert in einem gewissen Sinne der Grenzwert des arithmetischen Mittels  ¹/_n·(x₁ + ... + x_n)  ist.

Ein Beispiel dafür:  X  könnte für die Augenzahl beim Würfeln stehen. Dann sind  x₁, ..., x_n  zufällig gewürfelte Augenzahlen mit dem arithmetischen Mittel  ¹/_n·(x₁ + ... + x_n). Mit wachsendem  n  nähert sich dieser empirische Mittelwert dem theoretischen Erwartungswert  E(X) = 3.5 .

Wie lässt sich die Grenzwertaussage quantitativ fassen? Für ein  h > 0  definieren wir das Ereignis



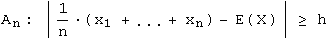
mit der Wahrscheinlichkeit  p(A_n). Dann gilt



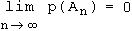
Also wird die Wahrscheinlichkeit für jede noch so kleine Abweichung  h  zwischen empirischem Mittelwert und theoretischem Erwartungswert mit wachsendem  n  beliebig klein.

Die Grenzwertaussage lässt noch offen, wie schnell  p(A_n)  gegen 0 strebt. Dazu benötigt man die Varianz  V(X); mit der folgenden Formel erkennt man, dass die Konvergenz linear mit  n  oder schneller ist:



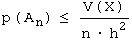
Im Würfel-Beispiel gilt  V(X) = 35/12 . Setzt man z.B. die Abweichung mit  h = 0.5  fest, erhält man



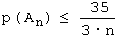
Würfelt man also  n = 1000  mal, so weicht der Mittelwert aller gewürfelten Augenzahlen nur noch höchstens mit Wahrscheinlichkeit  35/3000 = 0.011666 ...  um mindestens  0.5  von  3.5  ab. Die entsprechende umgekehrte Aussage ist noch deutlicher: Mit Wahrscheinlichkeit von mindestens  0.988333...  liegt der Mittelwert zwischen  3  und  4 .

Die Graphik auf der Briefmarke soll diesen Sachverhalt illustrieren, ist aber etwas karg beschriftet. Auf der waagerechten Achse ist  n  abgetragen, auf der senkrechten Achse der Mittelwert  ¹/_n·(x₁ + ... + x_n). Eigentlich müsste dann der Graph aus einzelnen Punkten bestehen, da nur ganzzahlige  n  sinnvoll sind, aber der Graphiker hat diese Punkte durch Strecken miteinander verbunden, was nicht unüblich ist und zu dem "gezackten" Verlauf des Graphen führt. Die waagerechte Linie oberhalb von "Helvetia" schneidet die senkrechte Koordinatenachse beim Erwartungswert  E(X). Der Graph soll nun die Annäherung des Mittelwerts an den Erwartungswert darstellen. Allerdings ist dies nicht sehr überzeugend gelungen. Die Ausschläge nach oben und unten nehmen in der rechten Hälfte kaum ab. Vor allem aber ist es überhaupt nicht charakteristisch für den Verlauf der Mittelwerte, dass der Graph mit jedem  n  immer abwechselnd steigt und fällt und dazu noch abwechselnd oberhalb und unterhalb von  E(X)  liegt. Eine Simulation mit Zufallszahlen (hier beispielhaft im Intervall  (0,1)  mit  E(X) = 0.5 ) gibt ein realistischeres Bild: