2020-11-14
Partitionen natürlicher Zahlen
Formel von Hardy-Ramanujan-Rademacher Kommentare sind willkommen.
Srinivasa Ramanujan und Godfrey Harold Hardy publizierten 1918 eine Formel für die Partitionsfunktion \(~P(n)\), die die Anzahl der Partitionen einer natürlichen Zahl \(~n~\) angibt [1]. Am Anfang dieser Arbeit stand die bewundernswerte zahlentheoretische Intuition Ramanujans; Hans Rademacher veröffentlichte 1937 eine Weiterentwicklung der Formel in eine besser handhabbare Gestalt [3]; beide Varianten findet man unter den Stichworten Formel von Hardy-Ramanujan-Rademacher und Approximation der Partitionsfunktion.
Fredrik Johansson gab in [2] eine Wertung der Formel: "One of the most astonishing number-theoretical
discoveries of the 20th century is the Hardy-Ramanujan-Rademacher formula first given as an
asymptotic expansion by Hardy and Ramanujan in 1917 and subsequently refined
to an exact representation by Rademacher in 1936, which provides a direct and
computationally efficient expression for the single value P(n)."
Diese Formel für \(~P(n)~\) ist eine asymptotische Summenformel. Man kann sie mit etwas Wohlwollen als "geschlossene Formel" akzeptieren, weil sie die Berechnung von \(~P(n)~\) "direkt" und exakt und mit endlich vielen Summanden erlaubt. Damit ist sie von ganz anderer Natur als konkurrierende Verfahren mittels Rekursion oder erzeugender Funktion, bei denen der Algorithmus die Gesamtheit der Werte \(~P(1)~...~P(n)~\) ausgibt. Die Anzahl der Summanden in der Formel ist nicht konstant, daher mag man die Bezeichnung der Formel als "geschlossen" in Frage stellen. - Ganz unabhängig von diesen Bezeichnungsfragen stellt die Formel von Hardy-Ramanujan-Rademacher einen Meilenstein der Kombinatorik, der Zahlentheorie und der Numerik dar.
Die ersten Glieder der Folge \(~P(n)~\) findet man in OEIS A000041 .
Nun zur Formel selbst: Wir geben direkt die "rechnergeeignete" Umformung an (Johansson [2] (1.4), (1.5), (2.1)) :
\[\text{(1)}~~~P(n)=~\left\langle\frac{4}{24n-1} \sum_{k=1}^{k_n} A_{nk}\cdot U_{nk}\right\rangle\]
\(\langle..\rangle\) steht für ganzzahlige Rundung.
\[A_{nk}=\sum_{L=0 \atop {n+L(3L+1)/2~=~0~\text{mod}~k}}^{2k-1} (-1)^L~\text{cos}\left(\frac{6L+1}{6k} \pi \right)\]
\[U_{nk}=\text{cosh}~C_{nk} - \frac{\text{sinh}~C_{nk}}{C_{nk}}~~~~~\text{mit}~~~~~C_{nk}=\frac{\pi~\sqrt{24n-1}}{6k}\]
\(k_n\) kann als \(~\text{max}~\{~9,~\lceil\sqrt{n}~\rceil~\}~\) genommen werden; mit weniger Summanden kommt man aus, wenn man Johansson [2] (1.8) anwendet:
\[\text{(2)}~~~\text{Wähle kleinstes}~~k_n~~\text{mit}~~\frac{44~\pi^2}{225 \sqrt{3~k_n}}+\frac{\pi}{75}~\sqrt{\frac{2~k_n}{n-1}}~~\text{sinh}~\left(\frac{\pi}{k_n}~\sqrt{\frac{2n}{3}}\right)\lt\frac{1}{2}\]
Wegen \(~\lim_{x \to \infty} (a/x +b~x~\text{sinh}(c/x^2))=0~\) findet man mit \(x=\sqrt{k_n}~\) schnell ein passendes \(~k_n\).
In der Summe für \(~A_{nk}~\) kommen wegen der Einschränkung \(~n+L(3L+1)/2 = 0 ~\text{mod}~k~\) nur ~\(\sqrt{k}~\) Summanden vor (Johansson [2] 2.1); die zugehörigen \(~L~\) werden weiter unten im Programm (Liste t2 ) als "erlaubte L" bezeichnet.
Im Programm wird die Summation nur über Summanden \(~k~\) durchgeführt, bei denen \(~A_{nk}~\) nicht die leere Summe (\(=0~\)) ist, denn es kommt häufig vor, dass es keine erlaubten \(~L~\) gibt. So ist im Programm "benötigte k" (Liste t3 ) zu verstehen.
Die Hardy-Ramanujan-Rademacher-Formel ist in verschiedenen Programmiersprachen implementiert worden. Johansson macht in [2] detaillierte Angaben zu Optimierung, Komplexität und numerischer Evaluation des Algorithmus. Er zeigt, dass eine Berechnung von \(~P(10^{15})~\) schon 2012 in etwa einer halben Stunde Rechenzeit möglich war. So ist es denn auch nicht verwunderlich, dass der Mathematica-Befehl PartitionsP erstaunlich schnell ist (wir wissen nichts über den verwendeten Algorithmus). - Diese Angaben lassen vermuten, dass auch eine einfache, nicht-optimierte Programmierung von (1) brauchbare Ergebnisse liefert, d.h. dass damit \(~P(n)~\) für "sehr große" (also weit über "Alltagsbedürfnisse" hinausgehende) \(~n~\) schnell berechnet werden kann.
Um einen Vergleich mit den optimierten Programmen in [2] ch. 4 zu ermöglichen, wird hier Mathematica 7 eingesetzt. Es soll gezeigt werden, wie (1) direkt in ein kurzes, leicht durchschaubares Programm umgesetzt werden kann - fernab aller Effizienzerwägungen der theoretischen Informatik:
(* Hardy-Ramanujan-Rademacher: Berechnung von P(n) *)
n = 53; (* n > 1 *) kn = 9; (* Anzahl Summanden *)
(* Liste t2 der erlaubten L : *)
t1 = Table[Mod[n+L(3 L+1)/2,k],{k,kn},{L,0,2k-1}];
t2 = Table[Flatten[Position[t1[[k]],0]]-1,{k,kn}];
(* Liste t3 der benötigten k : *)
anzt2 = Table[Length[t2[[k]]],{k,kn}];
t3 = Complement[Range[kn],Flatten[Position[anzt2,0]]];
A = Table[Sum[(-1)^t2[[k]][[j]] Cos[(6 t2[[k]][[j]]+1) Pi/(6 k)],{j,anzt2[[k]]}]/.k->t3[[i]],{i,Length[t3]}];
c = Pi Sqrt[24 n-1]/(6 k);
U = Table[Cosh[c]-Sinh[c]/c/.k->t3[[i]],{i,Length[t3]}];
pn = Round[(4/(24 n-1)) Plus@@(A U)]
329931
Das Ergebnis \(~P(n)=329.931~\) wird ohne bemerkbare Wartezeit ausgegeben.
Falls man für große \(~n~\) mit weniger als \(~\text{max}~\{~9,~\lceil\sqrt{n}~\rceil~\}~\) Summanden auskommen möchte, setzt man (2) in Mathematica um:
(* Bestimmung kn *)
n = 53;
Do[If[44 Pi^2/(225 Sqrt[3 N1])+Pi Sqrt[2 N1] Sinh[Pi Sqrt[2 n]/(N1 Sqrt[3])]/(75 Sqrt[n-1])<.5, kn = N1; Break[]], {N1,4 n}]
kn
9
Das Ergebnis \(~k_n=9~\) wird natürlich ohne bemerkbare Wartezeit ausgegeben; aber auch noch für \(~n=10^{12}~\) dauert die Berechnung von \(~k_n~\) nur wenige Sekunden.
Das Programm wird leichter durchschaubar, wenn man sich die Tabellen t1, t2, t3 ausgeben lässt.
t1 enthält für jeden Summanden k die Werte von Mod[n+L(3L+1)/2,k] :
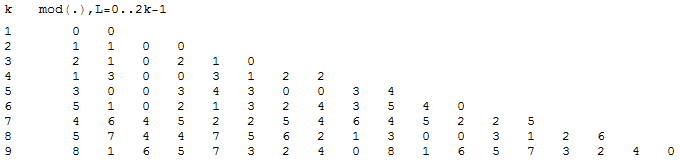
In t2 stehen für jedes k diejenigen L , die in t1 den modulo-Wert 0 haben; darunter steht t3 , also die Menge der k aus t2 , bei denen die L nicht die leere Menge bilden:

Dass dieses Programm für praktische Zwecke hinreichend schnell ist, soll im Folgenden gezeigt werden. Da die Programmläufe auf einem handelsüblichen Notebook Baujahr 2017 durchgeführt wurden, ist mit modernen Rechnern und Mathematica-Versionen sicherlich eine noch höhere Geschwindigkeit zu erwarten.
Die Laufzeit steigt keineswegs monoton mit \(~n~\) an. Diese Beobachtung korrespondiert mit den sehr schwankenden Anzahlen der im Programm verwendeten \(~k~\) und \(~L~\) (in den Tabellen t3 und t2 ). Dies wird anhand eines Beispiels deutlich:
n Stellen P(n) sec kn Anz. k Anz. L
7.000.000 2.940 23 942 463 2226
7.000.001 2.940 13 942 289 1098
7.000.002 2.940 20 942 430 1900
7.000.003 2.940 19 942 406 1776
7.000.004 2.940 19 942 436 1780
7.000.005 2.940 41 942 639 2870
7.000.006 2.940 15 942 329 1370
7.000.007 2.940 16 942 363 1578
7.000.008 2.940 18 942 404 1748
7.000.009 2.940 17 942 413 1604
Die drittletzte Tabellenspalte zeigt die mit dem Programm "Bestimmung kn" (s.o.) berechnete Anzahl der Summanden in (1). Das sind schon deutlich weniger als bei der gröberen Obergrenze \(~\text{max}~\{~9,~\lceil\sqrt{n}~\rceil~\}=2646~\). Aber auch diese \(~942~\) Summanden werden nicht alle benötigt, wie die vorletzte Spalte zeigt, die die Werte aus t3 enthält. In der inneren Summe \(~A_{nk}~\) in (1) entfallen die meisten \(~L~\); die Anzahl der benötigten \(~L~\), aufsummiert über alle \(~k~\), findet sich in der letzten Spalte. - Man sieht in der dritten Spalte die stark schwankende Rechenzeit bei wachsendem \(~n~\); das ist auch nicht verwunderlich, da die Anzahl der zu berechnenden Summanden in den beiden letzten Spalten sehr volatil ist und mit der Rechenzeit hoch korreliert.
Hier ist eine Tabelle für größere \(~n~\):
n Stellen P(n) sec kn Anz. k Anz. L
10.000.000 3.515 26 1.110 466 2.020
20.000.000 4.974 129 1.529 844 4.388
30.000.000 6.094 218 1.844 1.062 5.744
40.000.000 7.038 273 2.107 1.177 5.850
50.000.000 7.869 336 2.336 1.226 6.080
60.000.000 8.621 367 2.543 1.162 5.952
70.000.000 9.312 469 2.731 1.283 7.102
80.000.000 9.956 403 2.906 1.075 5.132
90.000.000 10.560 616 3.070 1.386 7.652
100.000.000 11.132 600 3.224 1.276 6.652
Trotz der wesentlich größeren Sprünge in \(~n~\) wächst die Rechenzeit in der dritten Spalte nicht monoton.
In diesem Bereich \(~n=10^7 ... 10^8~\) wächst die Stellenzahl von \(~P(n)~\) wie ~\(1,11~\sqrt{n}~\), das war zu erwarten wegen der asymptotischen Hardy-Ramanujan-Formel\[~P(n)\approx\frac{e^{\pi~\sqrt{\frac{2~n}{3}}}}{4~\sqrt{3}~n}~~~\Rightarrow~~~\text{Stellenzahl}~P(n)\approx 1,114~\sqrt{n}-log_{10}~n-0,84~\]
\(~k_n~\) wächst in diesem Bereich wie ~\(0,3~\sqrt{n}~\).
Literatur
[1] Hardy, G. H., Ramanujan, S., Asymptotic formulae in combinatory analysis, Proc. London Math. Soc., 2nd Series, 17 (1918), p. 75 - 115. Reprinted in Collected Papers of Srinivasa Ramanujan, Amer. Math. Soc. (2000), p. 276 - 309
[2] Johansson, F., Efficient implementation of the Hardy-Ramanujan-Rademacher formula, LMS J. Comp. Math., 15 (2012), p. 341 - 359
[3] Rademacher, H., On the partition function p(n), Proc. London Math. Soc., 2nd Series, 43/4 (1937), p. 241 - 254
Kommentare sind willkommen.
Stand 2020-08-13
Inhalt Blog | voriger Eintrag | nächster Eintrag
Manfred Börgens | Zur Leitseite Datenschutz
ab 2020-06-25
www.boergens.de/manfred/blog/blog005.htm
 MB Matheblog # 5
MB Matheblog # 5 MB Matheblog # 5
MB Matheblog # 5
