2020-09-27
Teilbarkeit eines Produkts von \(m\) Zahlen durch \(p^r\) , \(p\) prim Kommentare sind willkommen.
\(m\) paarweise verschiedene natürliche Zahlen aus \(\{1, 2,..., n\}\) werden zufällig ausgewählt. Wie groß ist die Wahrscheinlichkeit, dass ihr Produkt durch \(p^r\) mit \(p\) prim und \(r \in N\) teilbar ist?
Eine äquivalente Formulierung ist: Wie groß ist die Wahrscheinlichkeit, dass die \(m\) Zahlen den Primfaktor \(p\) insgesamt mindestens \(r-\)mal enthalten?
Diese Frage können wir beantworten, wenn wir zuerst die Wahrscheinlichkeit \(P(r)\) bestimmen, mit der die \(m\) Zahlen (bzw. ihr Produkt) den Primfaktor \(p\) insgesamt genau \(r-\)mal enthalten. \(P\) ist dann eine Wahrscheinlichkeitsverteilung.
Eine mögliche Anwendung für diese Verteilung als Testverteilung eines nichtparametrischen Hypothesentests ist die Prüfung der Nullhypothese "Zufälligkeit" bei Zahlenfolgen, z.B. bei Stichprobenziehungen in der Qualitätssicherung. Siehe dazu Abschnitt V.
I. Berechnung von \(P(r)\) .
\[\text{(1)}~~~P(r) = \frac{A_r}{\binom{n}{m}}\]
Dabei steht \(\binom{n}{m}\) für die Anzahl möglicher Auswahlen von \(m\) verschiedenen Zahlen aus \(n\) verschiedenen Zahlen ohne Berücksichtigung der Reihenfolge (im Folgenden nur mit "Auswahlen" bezeichnet). \(A_r\) sei die Anzahl derjenigen Auswahlen, die \(p\) genau \(r-\)mal enthalten.
Für die Berechnung von \(A_r\) wollen wir die zugehörigen Auswahlen danach unterscheiden, wie sich die \(r\) Primfaktoren \(p\) auf die \(m\) ausgewählten Zahlen verteilen. Dies führt auf Partitionen (die auch die Grundlage anderer Hypothesentests bilden, wie z.B. für den Rangsummentest von Wilcoxon/Mann/Whitney und den Wilcoxon-Vorzeichen-Rang-Test). Partitionen nehmen die zentrale Rolle bei der Berechnung von \(A_r\) ein. In dem hier behandelten Fall handelt es sich um die Zerlegung von \(r\) in maximal \(m\) positive ganzzahlige Summanden. Dazu zwei Beispiele:
Für \(m=9\) und \(r=6\) gibt es \(11\) Partitionen; das sind alle Partitionen von \(6\) , da \(m \geq r\) :
\(\{1,1,1,1,1,1\}\)
\(\{1,1,1,1,2\}\)
\(\{1,1,1,3\}\)
\(\{1,1,2,2\}\)
\(\{1,1,4\}\)
\(\{1,2,3\}\)
\(\{1,5\}\)
\(\{2,2,2\}\)
\(\{2,4\}\)
\(\{3,3\}\)
\(\{6\}\)
Für \(m=3\) und \(r=6\) kommen nicht alle Partitionen von \(6\) in Frage; übrig bleiben \(7\) Partitionen:
\(\{1,1,4\}\)
\(\{1,2,3\}\)
\(\{1,5\}\)
\(\{2,2,2\}\)
\(\{2,4\}\)
\(\{3,3\}\)
\(\{6\}\)
Wozu werden diese Partitionen benötigt? Wir nummerieren sie (in beliebiger Reihenfolge) mit \(R^{(r)}_1,R^{(r)}_2,~...,R^{(r)}_i,~...\) . Die Menge der Auswahlen, die \(p\) genau \(r-\)mal enthalten, bezeichnen wir mit \(M^{(r)}\) . Diese Menge zerfällt in disjunkte Teilmengen \(M^{(r)}_i\) , die sich bijektiv den Partitionen \(R^{(r)}_i\) zuordnen lassen:
\(M^{(r)}_i\) enthält diejenigen Auswahlen, in denen die vorkommenden Primfaktoren \(p\) genau die Potenzen in den einzelnen ausgewählten Zahlen haben, die den Elementen der Partition \(R_i\) entsprechen.
Im obigen ersten Beispiel ist \(R_5=\{1,1,4\}\) . \(M^{(6)}_5\) besteht dann aus allen Auswahlen, die genau zwei Zahlen mit Primfaktor \(p\) in erster Potenz und genau eine Zahl mit \(p\) in vierter Potenz enthalten (die anderen drei Zahlen sind dann teilerfremd zu \(p\) ), z.B. für \(p=3\) und \(n=100\) die Auswahl \(\{6,19,57,61,81,95\}\).
Für \(A_r\) in (1) gilt dann
\[\text{(2)}~~~A_r=|M^{(r)}|=\sum_i |M^{(r)}_i|\]
\(|..|\) steht für die Anzahl der Elemente. In (2) gehört der \(i-\)te Summand zur Partition \(R^{(r)}_i\) ; für diese Partition werden die zugehörigen Auswahlen in \(M^{(r)}_i\) gezählt.
Also ist der nächste Schritt die Berechnung von \(|M^{(r)}_i|\) . Wir führen folgende Bezeichnungen ein:
\(n_j\) Anzahl der durch \(p^j\) teilbaren Zahlen in \(\{1, 2,..., n\}\)
\(c^{(r)}_{ij}\) Anzahl der Elemente \(=j\) in \(R^{(r)}_i\)
\(c^{(r)}_{i0}=m-|R^{(r)}_i|\)
\(c^{(r)}_{i0}\) ist also die Anzahl der zu \(p\) teilerfremden Zahlen in den Auswahlen in \(M^{(r)}_i\) .
Nun ist \(n_j-n_{j+1}\) die Anzahl der Zahlen in \(\{1, 2,..., n\}\) , die \(p\) in genau \(j-\) ter Potenz enthalten. Von diesen müssen \(c^{(r)}_{ij}\) Zahlen ausgewählt werden (\(~j=0,1,~...,~r~\)) .
Damit erhalten wir:
\[\text{(3)}~~~|M^{(r)}_i|=\prod \limits_{j=0}^r \binom{n_j-n_{j+1}}{c^{(r)}_{ij}}\]
Wir fassen bis zu diesem Teilergebnis zusammen: In (3) betrachten wir die Anzahl von Auswahlen ("\(m\) aus \(n\)"), in denen genau \(r\) Primfaktoren \(p\) vorkommen und diese gemäß der \(i-\)ten Partition auf die \(m\) Zahlen verteilt sind - so wie im Beispiel oberhalb von (2). Im Produkt steht der \(j-\)te Faktor für die Anzahl aller Auswahlen von Zahlen, die \(p\) in genau der \(j-\)ten Potenz enthalten.
\[\text{(4)}~~~n_j=\left\lfloor \frac{n}{p^j}\right\rfloor\]
In (4) ist \(\lfloor ..\rfloor\) die ganzzahlige Abrundung. - Mit (2) erhalten wir das Ergebnis
\[\text{(5)}~~~A_r=\sum \limits_i \prod \limits_{j=0}^r \binom{\left\lfloor \frac{n}{p^j}\right\rfloor - \left\lfloor \frac{n}{p^{j+1}}\right\rfloor}{c^{(r)}_{ij}}\]
Mit (1) folgt die Wahrscheinlichkeitsverteilung :
\[\text{(6)}~~~P(r)=\frac{\sum \limits_i \prod \limits_{j=0}^r \binom{\left\lfloor \frac{n}{p^j}\right\rfloor - \left\lfloor \frac{n}{p^{j+1}}\right\rfloor}{c^{(r)}_{ij}}}{\binom{n}{m}}\]
Die Summe in (5) und (6) läuft über den Index \(i\) für die Zählung der Partitionen.
Wie berechnet man \(c^{(r)}_{ij}\) ? Eine geschlossene Formel für die Partitionen gibt es nicht. Deshalb ist ein CAS hier hilfreich; z.B. Mathematica gibt die benötigten Partitionen mit IntegerPartitions[r, m] aus, so dass
Count[IntegerPartitions[r, m][[i]], j]] die \(c^{(r)}_{ij}\) für \(j \ge 1\) liefert; \(c^{(r)}_{i0}\) wird mit m - Length[IntegerPartitions[r, m][[i]]] berechnet.
II. Definitionsbereich von \(P\)
\(P\) in (6) ist eine Wahrscheinlichkeitsverteilung für die Anzahl der Primfaktoren \(p\) in der Stichprobe. Welche \(r\) kommen dafür in Frage? Dazu greifen wir zunächst (4) nochmal auf:
\[\text{(7)}~~~n_j=\left\lfloor \frac{n}{p^j}\right\rfloor~~\text{ist die Anzahl der Zahlen in}~\{1, 2,..., n\}~~\text{mit mindestens}~~j~~\text{Primfaktoren}~~p\]
\[\text{(8)}~~~n_j^*=\left\lfloor \frac{n}{p^j}\right\rfloor-\left\lfloor \frac{n}{p^{j+1}}\right\rfloor~~\text{ist die Anzahl der Zahlen in}~\{1, 2,..., n\}~~\text{mit genau}~~j~~\text{Primfaktoren}~~p\]
In (7) und (8) ist ist der höchste auftretende Exponent \(j\) :
\[j_{max}=\left\lfloor \frac{ln~n}{ln~p}\right\rfloor\]
Die Anzahl der Stichprobenelemente mit mindestens bzw. genau \(j\) Primfaktoren \(p\) wollen wir mit \(r_j\) bzw. \(r_j^*\) bezeichnen. Mit (7) und (8) erhalten wir:
\[\text{(9)}~~~r=\sum \limits_{j=1}^{j_{max}} r_j~~~\text{und}~~~r_j\in \{max\{n_j-n+m,~0\}~,~...~,~min\{n_j,~m\}\}\]
\[\text{(10)}~~~r_j^*\in \{max\{n_j^*-n+m,~0\}~,~...~,~min\{n_j^*,~m\}\}\]
In (9) folgt die Summenformel aus
\[r=\sum \limits_{j=1}^{j_{max}} j\cdot r_j^* = \sum \limits_{j=1}^{j_{max}} j\cdot (r_j-r_{j+1})=\sum \limits_{j=1}^{j_{max}} j\cdot r_j -\sum \limits_{j=2}^{j_{max}+1} (j-1)\cdot r_j = \sum \limits_{j=1}^{j_{max}} r_j~~~\text{wegen}~~r_{j_{max}+1}=0\]
In (9) und (10) sollen die kleinsten Elemente \(max\{..\}\) erklärt werden: \(n-m\) Elemente der Grundgesamtheit sind nicht in der Stichprobe. Falls diese Anzahl von \(n\).. überschritten wird, muss (mindestens) der "Überstand" \(n\)..\(-(n-m)\) in der Stichprobe liegen.
Mit (9) erhält man den Definitionsbereich der Verteilung \(P\) :
\[r\in \left\{\sum \limits_{j=1}^{j_{max}} max\{n_j-n+m,~0\}~,~...~,~\sum \limits_{j=1}^{j_{max}} min\{n_j,~m\}\right\}\]
III. Beispiel
n = 12 m = 7 p = 2
Aus den ersten 12 natürlichen Zahlen (Grundgesamtheit) werden also 7 verschiedene Zahlen zufällig ausgewählt (Stichprobe); dafür gibt es 792 Möglichkeiten. In diesen 7 Zahlen wird der Primfaktor 2 gezählt.
jmax = 3 ist der höchste Exponent von 2 , der auftreten kann.
j nj n*j
1 6 3
2 3 2
3 1 1
Interpretation der Tabelle (siehe (7) und (8)):
j steht für die Exponenten von p = 2.
n2 = 3
bedeutet, dass in der Grundgesamtheit genau 3 Zahlen liegen, die durch p2 = 4 teilbar sind.
n*1 = 3
bedeutet, dass in der Grundgesamtheit genau 3 Zahlen liegen, die p = 2 exakt in 1. Potenz aufweisen.
Außerdem ergibt sich n*o = 6 aus n*o = n - n1 . (no = n = 12 ist trivial.)
Die folgende Tabelle gibt für rj aus (9) an, wieviele Stichprobenelemente durch 2j teilbar sein können:
r1 ∈ {1,..,6}
r2 ∈ {0,1,2,3}
r3 ∈ {0,1}
Die folgende Tabelle gibt für r*j aus (10) an, wieviele Stichprobenelemente genau j Primfaktoren 2 haben können (nur der Vollständigkeit halber; die r*j werden für die Verteilung P nicht benötigt):
r*1 ∈ {0,1,2,3}
r*2 ∈ {0,1,2}
r*3 ∈ {0,1}
Mit den ri ergibt sich der Definitionsbereich für P (kleinste und größte Elemente in der Tabelle der ri werden addiert):
r ∈ {1, 10}
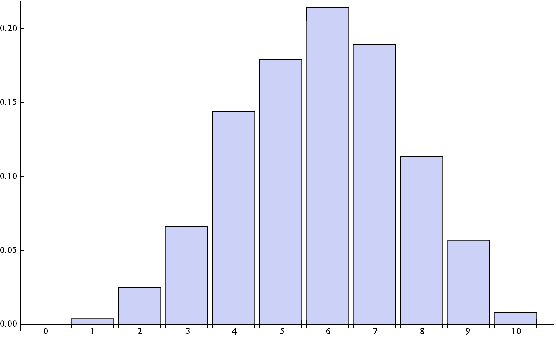
Wahrscheinlichkeitsverteilung:
r P(r)
1 0,0038
2 0,0253
3 0,0657
4 0,1439
5 0,1793
6 0,2146
7 0,1894
8 0,1136
9 0,0568
10 0,0076 Erwartungswert 5,8333 Standardabweichung 1,7588
Der entscheidende Schritt in (5) und (6) ist die Berechnung der c(r)ij . Beispielhaft soll das für r = 3 vollständig durchgeführt werden:
i R(3)i |R(3)i| c(3)i0 c(3)i1 c(3)i2 c(3)i3
Partition # 1 {1,1,1} 3 4 3 0 0
Partition # 2 {1,2} 2 5 1 1 0
Partition # 3 {3} 1 6 0 0 1
In A3 aus (5) wird in jedem der 3 Summanden (sie stehen für die 3 Partitionen) n*0 = 6 (für die 6 ungeraden Zahlen), n*1 = 3 (für 2, 6, 10), n*2 = 2 (für 4, 12) und n*3 = 1 (für 8) an die oberen Positionen der Binomialkoeffizienten gesetzt. Dann ist P(3) = A3/792 .
A3 =
\[~~~~~~~\binom{6}{4} \binom{3}{3} \binom{2}{0} \binom{1}{0} + \binom{6}{5} \binom{3}{1} \binom{2}{1} \binom{1}{0} + \binom{6}{6} \binom{3}{0} \binom{2}{0} \binom{1}{1}\]
= 15 + 36 + 1 = 52 → P(3) ≈ 0,0657
IV. Ursprüngliche Fragestellung
Ganz am Anfang stand die Frage nach der Wahrscheinlichkeit, dass das Produkt der \(m\) Zahlen durch \(p^r\) teilbar ist; diese Wahrscheinlichkeit wollen wir \(P^*(r)\) nennen. Die Frage ist nun mit (6) leicht zu beantworten:
\[P^*(r)=\sum_{s\ge r} P(s)=1-F(r-1)\]
\(F\) steht für die kumulierte Verteilung zu \(P\) .
Im Beispiel in Abschnitt III. ist dann P*(3) = 0,9709 die Wahrscheinlichkeit dafür, dass das Produkt von 7 verschiedenen zufällig ausgewählten natürlichen Zahlen ≤ 12 durch 8 teilbar ist.
V. Anwendung
Hier ist eine mögliche Anwendung für die Verteilung \(P\) als Testverteilung eines nichtparametrischen Hypothesentests: Tests auf Zufälligkeit benötigen eine möglichst große Vielfalt, da sich Zufälligkeit nicht durch einige wenige willkürlich ausgewählte Verfahren "erhärten" lässt (sie lässt sich aber sehr wohl durch ein einzelnes Testergebnis zu Fall bringen - natürlich immer mit einer Irrtumswahrscheinlichkeit). In der Regel wird man eine umfangreiche Batterie von Tests anwenden wollen, die auf viele ganz verschiedene Merkmale von Zufälligkeit zielen. Bei der hier vorgestellten Fragestellung geht es um die Auswahl von Zahlen aus einer Grundmenge. Beispiele können sein:
- Lottozahlen
- Stichprobenziehungen in der Qualitätssicherung
Dafür sind zahlreiche Hypothesentests denkbar; z.B. können als Teststatistik arithmetisches Mittel, Minimum/Maximum, Anzahl "Runs" usw. dienen. Die hier diskutierte Wahrscheinlichkeitsverteilung \(P\) trägt einen weiteren statistischen Test auf Zufälligkeit der Auswahl von Zahlen bei.
Beispiel
Eine in Serienproduktion hergestellte Platine hat 100 Lötstellen. In jeder Platine werden 3 zufällig ausgewählte Lötstellen überprüft. Für die Auswahl wird ein Algorithmus programmiert, dessen Zufälligkeit getestet werden soll. Dafür kann man die Verteilung P heranziehen (sinnvollerweise natürlich im Verbund mit anderen Tests). Die Nullhypothese lautet dann: "Die Anzahl r der Primfaktoren p in der Auswahl der (nummerierten) Lötstellen ist zufällig". Für p = 2 erhält man die folgende Testverteilung:
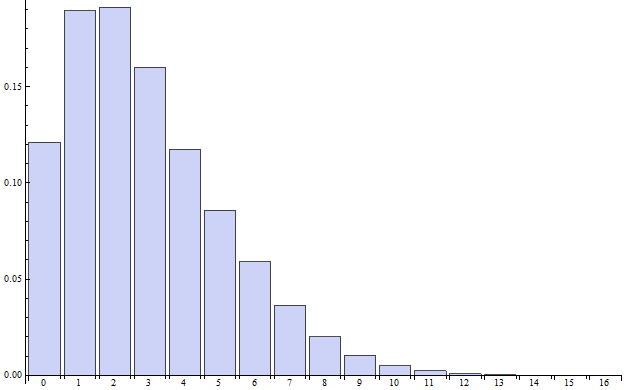
Hier ist F(7) ≈ 0,96 , also würde bei einem rechtsseitigen Test und einer vorgegebenen Irrtumswahrscheinlichkeit von α = 0,05 jedes r ≥ 8 zur Ablehnung der Nullhypothese führen (etwa bei der Auswahl {16,20,94} mit r = 8 oder im Extremfall {32,64,96} mit r = 16 ). Das Testergebnis würde sich dann so lesen: "Die Auswahl der Zahlen weist den Faktor 2 überdurchschnittlich häufig auf".
Dieser Test scheint nicht recht überzeugend. Erst wenn sich ein solches Ergebnis wiederholt zeigen sollte, würde man zur Annahme der Nicht-Zufälligkeit neigen. Außerdem würde man wohl auch zusätzlich andere Primfaktoren für Tests heranziehen.
Überzeugender erscheint ein anderer Ansatz: Man sammelt die \(r-\)Werte von zahlreichen Auswahlen und vergleicht die daraus resultierende empirische Häufigkeitsverteilung mit der Testverteilung; z.B. mit einem \(\chi^2-\)Anpassungstest.
Kommentare sind willkommen.
Stand 2020-08-03
Inhalt Blog | voriger Eintrag | nächster Eintrag
Manfred Börgens | Zur Leitseite Datenschutz
ab 2020-06-25
www.boergens.de/manfred/blog/blog004.htm
 MB Matheblog # 4
MB Matheblog # 4 MB Matheblog # 4
MB Matheblog # 4
