Problem des Monats September 2003

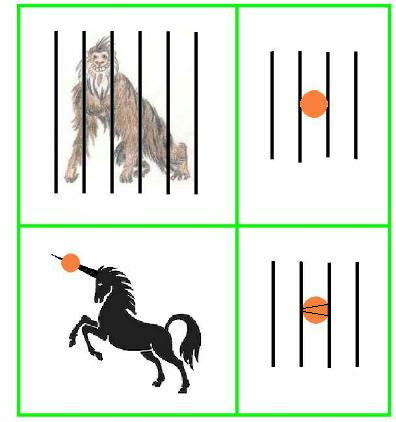
Hypatia besucht den Zoo für seltene Tiere in Alexandria. Dem Yeti möchte sie eine Orange schenken, aber leider passt diese nicht durch die Gitterstäbe (Abstand 7 cm). Hypatia ist in der Schule gut in Mathematik und hat eine Idee. Sie bittet das Einhorn im Nachbargehege, sein Horn herauszustrecken. Hypatia spießt die Orange auf das Horn (sehr spitz, Winkel an der Spitze 10°), schön symmetrisch durch die Mitte wie im Bild, und zieht sie wieder ab. Jetzt hat die Orange ein durchgehendes Loch und passt genau (ohne Spielraum) durch die Gitterstäbe des Yeti-Geheges.

Wieviel bekommt der Yeti von Hypatia zu fressen? (In Gramm; eine Orange hat 4/5 der Dichte von Wasser.)

Falls Sie keinen Lösungsansatz finden, können Sie hier einige Hinweise lesen.

Lösung

Die Orange wird näherungsweise als Kugel und das Horn als Kegel mit Öffnungswinkel 10° aufgefasst.

Was ist verblüffend an der Aufgabenstellung? Weder wird angegeben, wie groß die Orange ist, noch wie weit sie aufgespießt wird. Das kann nur bedeuten, dass diese Angaben keinen Einfluss auf das Ergebnis haben, also gilt der Satz (der weiter unten auch noch bewiesen wird):

Satz:
Alle Körper, die durch zentrale Kegelbohrung (mit festem Kegelöffnungswinkel) durch beliebige Kugeln entstehen und eine vorgegebene Bohrungshöhe aufweisen, haben das gleiche Volumen.

Der Satz hat Plausibilität: Der "Restkörper" hat in der Problemstellung die Breite  h = 7 cm ("Bohrungshöhe"), und diese lässt sich erreichen, wenn man eine dicke Orange weit aufs Horn spießt (also viel wegbohrt) oder eine kleinere weniger weit (also weniger wegbohrt); der Satz besagt, dass jeweils das Volumen des Restkörpers gleich ist.

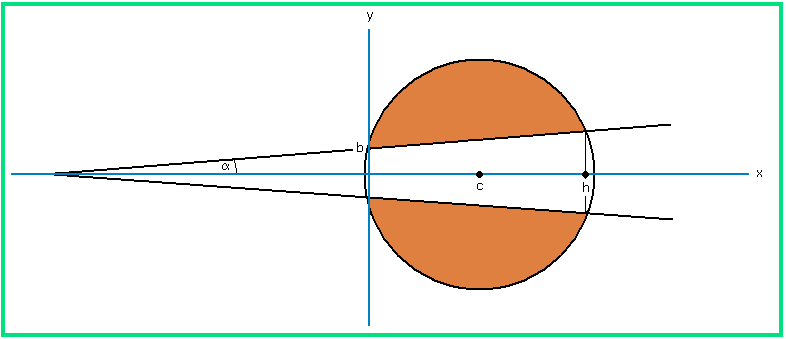
Bild 1

In Bild 1 ist die auf das Horn aufgespießte Orange schematisch im Querschnitt dargestellt. Dieser Querschnitt ist so in ein Koordinatensystem gelegt, dass die beiden linken Schnittpunkte des Kreises mit den Mantellinien des Kegels auf der y-Achse liegen. Der Winkel α ist der halbe Öffnungswinkel des Kegels, also hier α = 5°. Bei  y = b  schneidet die obere Mantellinie des Kegels die senkrechte Achse;  b  hängt davon ab, wie man den Kegelquerschnitt in das Koordinatensystem legt; man wird noch sehen, dass  b  nicht zahlenmäßig angegeben zu werden braucht. Der Kugelmittelpunkt liegt in  (x,y) = (c,0).  x = h  gibt die Breite des Restkörpers an (Bohrungshöhe). Hier ist  h = 7  (die Einheit für alle Längenangaben soll immer cm sein und wird nicht mitgeschrieben).

1. Lösungsweg (Spezialfall, geometrisch)

Wenn man aufgrund der Aufgabenstellung dem obigen Satz vertraut, liegt es nahe, einen möglichst einfachen Spezialfall zu betrachten (Bild 2). Der Restkörper ist hier eine Kugel, von der ein zentral liegender Kegel und ein Kugelabschnitt fehlen.

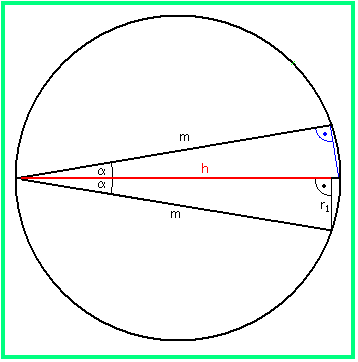
Bild 2

Man erhält aus dem unteren rechtwinkligen Dreieck in Bild 2  m = h/cos α, also hier  m = 7/cos 5°.

Ist  r  der Kugelradius, so ist  2r = m/cos α  (das obere rechtwinklige Dreieck ergibt sich nach dem Satz des Thales), also hier  2r = 7/cos² 5°.

Ist  r₁  der Bodenradius des Kegels, so ist  r₁ = h·tan α, also hier  r₁ = 7·tan 5°.

So ergibt sich (mit Hilfe einer Formelsammlung) das gesuchte Volumen (in cm³):

V = V_Kugel - V_Kegel - V_Abschnitt

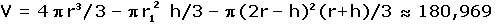
2. Lösungsweg (Spezialfall, mit Integralrechnung)

Wir gehen vom gleichen Grenzfall wie im 1. Lösungsweg aus. Der Restkörper ist ein Rotationskörper (orangene Querschnittfläche in Bild 3), sein Volumen kann als Integral berechnet werden.

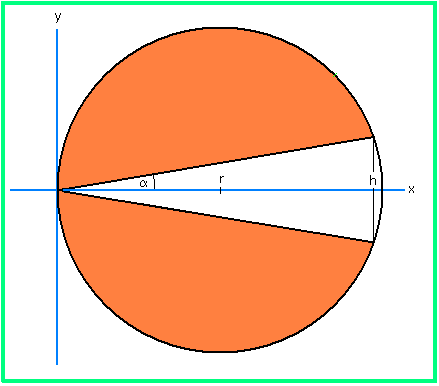
Bild 3

Geradengleichung der oberen Mantellinie:  y = g(x) = x·tan α
Kreisgleichung (oberer Halbkreis):  y = k(x) = (r² - (x-r)²)^1/2

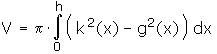
Man kann nun  r  wie im 1. Lösungsweg bestimmen und damit das Integral berechnen. Aber es geht auch einfacher:  k² - g²  ist ein Polynom 2. Grades mit führendem Koeffizienten  -(1+tan² α) = -1/cos² α = -1/cos² 5°  und mit den Nullstellen  x = 0  und  x = h = 7. Also ist der Integrand

k²(x) - g²(x) = -cos^-2 α ·x·(x-h) = -cos^-2 5° ·x·(x-7)

Man erhält das Volumen (in cm³):

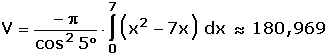
3. Lösungsweg (allgemeiner Fall)

Jetzt soll der Satz nicht mehr verwendet werden, vielmehr fällt sein Beweis bei diesem allgemeinen Lösungsweg mit ab.

Man geht aus von Bild 1, lässt aber  b, c  und den Kugelradius  r  unbestimmt, denn das Verfahren aus dem 2. Lösungsweg lässt sich auch hier anwenden:

Geradengleichung der oberen Mantellinie:  y = g(x) = x·tan α + b
Kreisgleichung (oberer Halbkreis):  y = k(x) = (r² - (x-c)²)^1/2

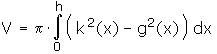
k² - g²  ist ein Polynom 2. Grades mit führendem Koeffizienten  -(1+tan² α) = -1/cos² α  und mit den Nullstellen  x = 0  und  x = h. Also ist der Integrand der gleiche wie im 2. Lösungsweg:

k²(x) - g²(x) = -cos^-2 α ·x·(x-h)

Man erhält

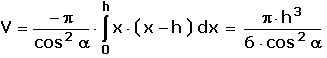
Dies ist die allgemeine Volumenformel für den obigen Satz. Man sieht, das Volumen hängt nur von der Bohrungshöhe  h  und dem halben Kegelöffnungswinkel  α  ab, nicht jedoch von  r, c  und  b.

Setzt man  α = 5°  und  h = 7  ein, erhält man wieder (gerundet)  V = 180,969.

Wieviel bekommt der Yeti zu fressen?

1 cm³ Wasser hat die Masse 1 Gramm, also erhält der Yeti  4/5  von ca. 180,969 Gramm, nämlich ca. 144,775 Gramm.