Wir wollen nun zwei Spielvarianten betrachten:
| Manfred Börgens Mathematische Probleme # 20 |
Liste aller Probleme mit Lösungen voriges Problem nächstes Problem |
zur Leitseite |
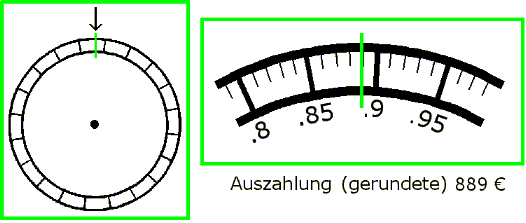
Das Glücksrad
Auf dem Rand dieses Glücksrads lassen sich Zahlen zwischen 0 und 1 ablesen. Wenn das Rad zum Stillstand kommt, wird die Zahl am Zeiger oben abgelesen und der Spieler erhält den entsprechenden Anteil von 1000 Euro. Der faire Einsatz für ein solches Spiel ist dann 500 Euro.

Wir wollen nun zwei Spielvarianten betrachten:
1. Das Maximumspiel
Der Spieler darf n-mal das Glücksrad drehen und erhält den maximalen Betrag der n Einzelspiele. Wie groß ist hier der faire Einsatz?
2. Das Risiko-Spiel
Der Spieler darf maximal n-mal das Glücksrad drehen. Er kann selbst bestimmen, welches sein letztes Einzelspiel ist; er erhält nur die Auszahlung aus diesem Spiel. Welches ist die optimale Strategie für das Risiko-Spiel? Wie groß ist der faire Einsatz?
Ein paar Anmerkungen, die Ihnen nützlich sein könnten - lesen Sie nicht weiter, wenn Sie glauben, auch alleine zurecht zu kommen.
Das Maximum-Spiel lässt sich leicht mit einem Programm simulieren. Aber auch die mathematische Behandlung ist nicht schwer, wenn man statt der Wahrscheinlichkeitsverteilung P(x), wo x das Maximum aus den n Spielen ist, zunächst die Verteilungsfunktion F(x) = Wahrscheinlichkeit(Maximum < x) ausrechnet. Aus der Stochastik ist der Zusammenhang zwischen P und F bekannt. Aus P ergibt sich dann der gesuchte Erwartungswert (fairer Einsatz).
Das Risiko-Spiel ist noch interessanter. Für n = 2 stellt sich lediglich die Frage, ob der Spieler beim ersten Mal zugreifen oder auf das letzte Spiel hoffen soll. Da der Erwartungswert für das letzte Spiel 500 Euro beträgt, lautet die optimale Strategie: Zugreifen beim ersten Einzelspiel, falls das Glücksrad einen Wert > 0.5 anzeigt. Diesen "Schwellenwert" nennen wir s 2 = 0.5 .
Für n = 3 geht man genauso vor. Was hat der Spieler im Mittel zu erwarten, falls er die erste Chance vorübergehen lässt? Aus dem Fall n = 2 wissen wir, dass er die zweite Chance mit Wahrscheinlichkeit 1 - s 2 = 0.5 nutzt; in diesem Fall kann er im Mittel mit 750 Euro rechnen. Nutzt er die zweite Chance nicht (Wahrscheinlichkeit s 2 ), erhält er im Mittel s 2 · 1000 Euro = 500 Euro. Somit lautet jetzt der Schwellenwert s 3 = 0.625.
Man erkennt, dass man zur Berechnung von s 3 nur s 2 benötigt. So fährt man induktiv fort, berechnet s 4 aus s 3 usw. bis s n. Die optimale Strategie lautet also: Hat man noch k Einzelspiele vor sich, so höre man beim nächsten Einzelspiel auf, wenn das Glücksrad dann mehr als s k anzeigt.
Nach welcher allgemeinen Formel ergibt sich s k + 1 aus s k ? Für große k finden Sie (evtl. mit Computerhilfe) eine einfache und gute Näherungsformel für s k .
Die optimale Strategie liefert den fairen Einsatz gleich mit.