Problem des Monats Juli / August 2001
Anke und Barbara sind die Spitzenspielerinnen in ihrem Tennisverein und spielen oft gegeneinander. Anke spielt etwas schwächer. Aufgrund der bisherigen Spielresultate geht sie davon aus, dass sie einen Satz gegen Barbara in vier von neun Fällen gewinnt.
Anke gehört auch dem Organisationskommittee für die nächste Vereinsmeisterschaft an. Sie rechnet damit, im Finale gegen Barbara antreten zu müssen. Als darüber diskutiert wird, ob das Finale über drei Sätze (zwei Gewinnsätze zum Sieg nötig) oder über fünf Sätze (drei Gewinnsätze nötig) gehen soll, ahnt Anke, dass sie ihre Chancen ein wenig beeinflussen kann.
Sollte sie für ein Dreisatzmatch oder für ein Fünfsatzmatch stimmen?
Lösung
Die Wahrscheinlichkeit, mit der Anke einen Satz gegen Barbara gewinnt, ist p = 4/9 .
Ein Tennisspiel wird nicht weiter fortgeführt, sobald eine Spielerin als Siegerin feststeht. Bei einem Dreisatzmatch steht also Anke bereits nach zwei Sätzen als Siegerin fest mit Wahrscheinlichkeit p2 ; und erst nach drei Sätzen mit Wahrscheinlichkeit
(1 - p)·p2 + p·(1 - p)·p = 2·p2·(1 - p) ,
denn dabei kommen nur die Varianten verloren / gewonnen / gewonnen und gewonnen / verloren / gewonnen in Frage.
Ähnlich geht es bei einem Fünfsatzmatch:
Anke gewinnt die ersten drei Sätze mit Wahrscheinlichkeit p3 , benötigt vier Sätze zum Sieg mit Wahrscheinlichkeit 3·p3·(1 - p) und fünf Sätze mit 6·p3·(1 - p)2 . Der Faktor 6 im letzten Term steht für die Anzahl der Möglichkeiten, die beiden verlorenen Sätze auf die ersten vier Sätze zu verteilen.
Insgesamt gewinnt Anke ein Dreisatzmatch mit Wahrscheinlichkeit 0.417 und ein Fünfsatzmatch mit Wahrscheinlichkeit 0.397 .
Anke hat also bessere Chancen in einem Dreisatzmatch.
Natürlich spielt es in Wirklichkeit keine Rolle, ob das Match nach dem entscheidenden Satz beendet wird oder nicht. Bezieht man jeweils alle drei bzw. fünf Sätze in die Betrachtung ein, so erhält man die binomialen Wahrscheinlichkeiten:
Für zwei gewonnene Sätze im Dreisatzmatch 3·p2·(1 - p) , für drei gewonnene Sätze im Dreisatzmatch p3 , für drei gewonnene Sätze im Fünfsatzmatch 10·p3·(1 - p)2 , für vier gewonnene Sätze im Fünfsatzmatch 5·p4·(1 - p) , für fünf gewonnene Sätze im Fünfsatzmatch p5 . Summiert man auf, so ergeben sich die selben Gewinnchancen für Anke wie oben.
Das lässt sich verallgemeinern:
In einem Spiel, das keine Unentschieden zulässt, hat der schwächere Spieler umso bessere Gewinnchancen, je weniger Runden gespielt werden.
Dies soll nun bewiesen werden (einen anderen Beweis, der früher an dieser Stelle stand, findet man hier).
Wir betrachten eine Serie von 2n + 3 Spielen. Mit Wahrscheinlichkeit p1 "dreht" sich das Gesamtergebnis in den letzten beiden Spielen zugunsten des schwächeren Spielers, nämlich wenn er genau n Siege aus den ersten 2n + 1 Spielen erzielt hat und dann die beiden letzten Spiele gewinnt. Mit Wahrscheinlichkeit p2 "dreht" sich das Gesamtergebnis in den letzten beiden Spielen zuungunsten des schwächeren Spielers, nämlich wenn er genau n + 1 Siege aus den ersten 2n + 1 Spielen erzielt hat und dann die beiden letzten Spiele verliert. In allen anderen Fällen, also mit Wahrscheinlichkeit 1 - p1 - p2 , gewinnt der schwächere Spieler genau dann in 2n + 3 Spielen, wenn er in 2n + 1 Spielen gewinnt. Zu zeigen ist somit nur p1 < p2 . In den folgenden
Formeln ist zur Abkürzung q = 1 - p gesetzt.
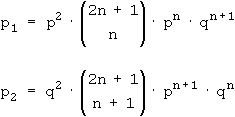
In diesen Formeln sind p2 bzw. q2 die Wahrscheinlichkeiten für zwei Siege bzw. zwei Niederlagen des schwächeren Spielers in den beiden letzten Spielen. Die Faktoren dahinter stammen aus der Binomialverteilung und geben die Wahrscheinlichkeit an, dass der schwächere Spieler genau n bzw. n + 1 Siege aus den ersten 2n + 1 Spielen erzielt. Man beachte, dass die beiden Binomialkoeffizienten denselben Wert haben. Durch Ausklammern erhält man:
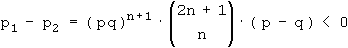
Stand 2005-05-26
voriges Problem | Liste aller Probleme mit Lösungen | nächstes Problem
Manfred Börgens | zur Leitseite