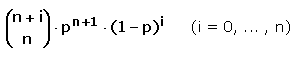
Insgesamt beträgt also die Gewinnwahrscheinlichkeit in 2n + 1 Runden
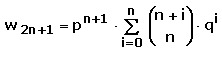
wenn man zur Abkürzung q = 1 - p setzt.
Alternativer Beweis zum Problem des Monats Juli / August 2001
In einem Spiel, das keine Unentschieden zulässt, hat der schwächere Spieler umso bessere Gewinnchancen, je weniger Runden gespielt werden.
Die Anzahl der Spielrunden ist ungerade (da es immer einen Sieger geben soll), kann also mit 2n + 1 bezeichnet werden. Hat ein Spieler pro Runde die Gewinnwahrscheinlichkeit p , so gewinnt er nach genau n + 1 Runden mit Wahrscheinlichkeit pn + 1 , nach n + 2 Runden mit Wahrscheinlichkeit (n + 1)·pn + 1·(1 - p) usw., allgemein erfolgt ein
Gewinn nach (n + 1) + i Runden mit Wahrscheinlichkeit
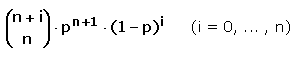
Insgesamt beträgt also die Gewinnwahrscheinlichkeit in 2n + 1 Runden
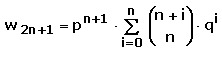
wenn man zur Abkürzung q = 1 - p setzt.
Um festzustellen, ob zwei Runden mehr (also 2n + 3) eine größere, gleiche oder kleinere Gewinnwahrscheinlichkeit erbringen, werden w2n + 1 und w2n + 3 verglichen. Es wird gezeigt:
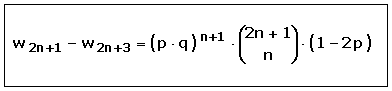
Daraus liest man ab:
p < 1/2 --> w2n + 1 > w2n + 3
p = 1/2 --> w2n + 1 = w2n + 3
p > 1/2 --> w2n + 1 < w2n + 3
Dies ist aber gerade die oben gemachte Behauptung, dass der schwächere Spieler umso bessere Gewinnchancen hat, je weniger Runden gespielt werden.
Die Formel im Kasten beweist man so:
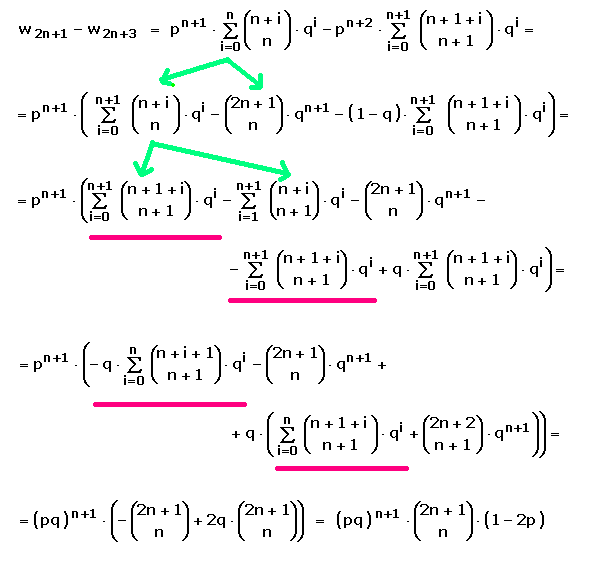
Manfred Börgens - Problem des Monats Juli/August 2001 - Alternativer Beweis - Stand 2005-05-26